Сфера Эвальда

Физический смысл обратной решетки

Обратная решетка является важным математическим образом, находящим многочисленные применения в геометрической кристаллографии, в теории дифракции и структурном анализе кристаллов, в физике твердого тела.

Например, понятие обратной решетки используется для описания периодического распределения отражающей способности кристалла по отношению к рентгеновским лучам. Отражение рентгеновских лучей от плоскостей структуры кристалла описывается формулой Вульфа-Брэгга, из которого следует, что при постоянной длине волны рентгеновского излучения l большому межплоскостному расстоянию для семейства параллельных отражающих плоскостей d отвечает малый угол падения q, т. е., чем больше межплоскостное расстояние, тем ближе направления отраженных лучей к направлению падающего пучка. Отражения рентгеновских лучей от бесконечно протяженных идеальных кристаллов должны быть точечными.

Каждый узел обратной решетки соответствует возможному отражению от плоскостей прямой решетки кристалла. Направление вектора обратной решетки H*_hkl совпадает с направлением отражения от плоскостей hkl в прямой решетке, а n-ый узел обратной решетки в этом ряду отвечает отражению n-го порядка от этих плоскостей.

Для предсказания углов поворота кристалла и направления дифрагированных лучей очень удобно пользоваться построением Эвальда.

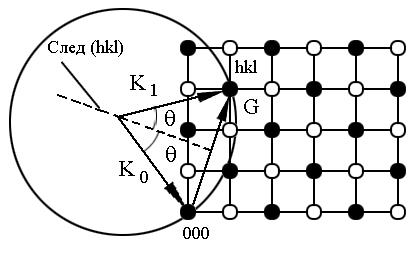Отложим волновой вектор k0 падающей на кристалл волны, так что его конец совпадет с узлом 0 0 0 обратной решетки. Поскольку частота и скорость рассеянной и падающей волны совпадают, вектор рассеянной волны k1 будет иметь ту же длину, что и k0, но неопределенное направление, тогда его удобно изобразить в виде сферы (сферы Эвальда) с центром в начале вектора k0. Начало и конец вектора рассеяния тогда будет соответственно концом вектора k0 и концом вектора k1. Теперь надо узнать, совпадет ли один из возможных векторов G с одним из узлов обратной решетки. Для этого следует совместить начальный узел обратной решетки с началом вектора рассеяния G (эта же точка - конец вектора k0) и посмотреть, попал ли один из узлов на сферу Эвальда. Ясно, что вероятность попадания одного из точечных узлов на сферу практически равна нулю, чтобы такое попадание имело место, необходимо повернуть кристалл и связанную с ним обратную решетку. Теперь уже с помощью геометрии можно вычислить необходимые углы поворота обратной решетки (и кристалла), а затем определить, под какими углами должен быть расположен детектор излучения, регистрирующий волны с вектором k1. Современные приборы для наблюдения дифракции - дифрактометры, снабженные ЭВМ, позволяют в автоматическом режиме, по формулам, описывающим повороты обратной решетки, вычислять нужные углы поворота кристалла и детектора излучения для заранее сориентированного кристалла, а затем поворачивать кристалл и детектор.

Дата добавления: 2015-04-24