Принимаемые значения: лрл

Принимаемые значения: лрл

Примеры:

1. Данный четырёхугольник — квадрат (A - и). Около данного четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - и).

2. Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник не квадрат, то около него можно описать окружность (A B - и).

3. Данный четырёхугольник — квадрат (A - и). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - л).

4. Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник не квадрат, то около него нельзя описать окружность (A B - и).

5. Операция эквиваленция (двойная импликация):

Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Обозначается: ол

В естественном языке: соответствует оборотам речи "тогда и только тогда"; "в том и только в том случае"

Примеры:

1. 24 делится на 6 (A - и). 24 делится на 3 (B - и). 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - и).

2. 24 не делится на 6 (A - л). 24 делится на 3 (B - и). 24 не делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л).

3. 24 делится на 6 (A - и). 24 не делится на 3 (B - л). 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л).

4. 24 не делится на 6 (A - л). 24 не делится на 3 (B - л). 24 не делится на 6 тогда и только тогда, когда 24 не делится на 3 (A B - и).

Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции —дизъюнкция (“или”) и в последнюю очередь — импликация и эквиваленция.

21)Операционная система является базовой и необходимой составляющей программного обеспечения компьютера (software). Операционная система обеспечивает управление всеми аппаратными компонентами компьютера (hardware). Другими словами, операционная система обеспечивает функционирование и взаимосвязь всех компонентов компьютера, а также предоставляет пользователю доступ к его аппаратным возможностям. К системному блоку компьютера подключаются через специальные согласующие платы (контроллеры) периферийные устройства (дисковод, принтер и т. д.). Каждое периферийное устройство обрабатывает информацию по-разному и с различной скоростью, поэтому необходимо программно согласовать их работу с работой процессора. Для этого в составе операционной системы имеются специальные программы — драйверы устройств. Каждому устройству соответствует свой драйвер.

Процесс работы компьютера в определенном смысле сводится к обмену файлами между периферийными устройствами, т. е. необходимо уметь управлять файловой системой. Ядром операционной системы является программа, которая обеспечивает управление файловой системой.

Пользователь общается с компьютером через устройства ввода информации (клавиатура, мышь). После ввода команды операционной системы специальная программа, которая называется командный процессор, расшифровывает команды и исполняет их.

Процесс общения пользователя с компьютером должен быть удобным. В состав современных операционных систем (Windows) обязательно входят модули, создающие графический интерфейс.

Таким образом, в структуру операционной системы входят следующие модули:

• базовый модуль, управляющий файловой системой;

• командный процессор, расшифровывающий и выполняющий команды;

• драйверы периферийных устройств;

• модули, обеспечивающие графический интерфейс.

Файлы операционной системы находятся на диске (жестком или гибком). Однако программы могут выполняться, только если они находятся в оперативной памяти, поэтому файлы операционной системы необходимо загрузить в оперативную память. Все файлы операционной системы не могут одновременно находиться в оперативной памяти, так как объем современных операционных систем составляет десятки мегабайт. Для функционирования компьютера обязательно должны находиться в оперативной памяти базовый модуль, командный процессор и драйверы подключенных устройств. Модули операционной системы, обеспечивающие графический интерфейс, могут быть загружены по желанию пользователя. В операционной системе Windows 95 выбор варианта загрузки представлен в виде меню.

После включения компьютера производится загрузка операционной системы в оперативную память, т. е. выполняется программа загрузки. Однако для того чтобы компьютер выполнял какую-нибудь программу, эта программа должна уже находиться в оперативной памяти. Выход из этого противоречия состоит в последовательной, поэтапной загрузке.

В соответствии с английским названием этого процесса — bootstrap, — система как бы «поднимет себя за шнурки ботинок». В системном блоке компьютера находится ПЗУ (BIOS), в котором содержатся программы тестирования компьютера и первого этапа загрузки операционной системы. После включения компьютера эти программы начинают выполйяться, причем информация о ходе этого процесса высвечивается на экране дисплея.

На этом этапе процессор обращается к диску и ищет на определенном месте (в начале диска) наличие очень небольшой программы-загрузчика BOOT. Программа-загрузчик считывается в память, и ей передается управление. В свою очередь она ищет на диске базовый модуль операционной системы, загружает его в память и передает ему управление.

В состав базового модуля операционной системы входит основной загрузчик, который ищет остальные модули операционной системы и загружает их в оперативную память.

В случае, если в дисковод вставлен несистемный диск или диск вообще отсутствует, на экране дисплея появляется соответствующее сообщение.

Вышеописанная процедура запускается автоматически при включении питания компьютера (так называемый «холодный» старт), однако часто используется процедура «перезагрузки» операционной системы («горячий» старт), которая происходит по нажатию на кнопку RESET или одновременного нажатия на клавиши + +

22)Законы логики отражают наиболее важные закономерно­сти логического мышления, В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствие с законами логики.

Закон тождества. Всякое высказывание тождественно са­мому себе: А = А

Закон непротиворечия. Высказывание не может быть од­новременно истинным и ложным. Если высказывание А — истинно, то его отрицание не А должно быть ложным. Сле­довательно, логическое произведение высказывания и его отрицания должно быть ложно: A & A = 0

Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означа­ет, что результат логического сложения высказывания и его отрицания всегда принимает значение истина: A v A = 1

Закон двойного отрицания. Если дважды отрицать неко­торое высказывание, то в результате мы получим исходное высказывание: A = A Кроме логических законов, важное значение для выполнения преобразований логических выражений имеют правила алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.

Законы Моргана: (A v B)= А & В

(A & B)= А v В

Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказыва­ний можноменять местами логические переменные при опе­рациях логического умножения и логического сложения:

Логическое умножение Логическое сложение

A & B = B & A A v B = A v B

Правило ассоциативности. Если в логическом выраже­нии используются только операция логического умножения или только операция логического сложения, то можно пре­небрегать скобками или произвольно их расставлять:

Логическое умножение Логическое сложение

(A & B) & C = A & (B & C) (A v B) v C = A v (B v C)

Правило дистрибутивности. В отличие от обычной алгеб­ры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:

Дистрибутивность умножения Дистрибутивность сложения

относительно умножения относительно сложения

(a x b) + (a x c) = a x (b + c)

(A & B) v (A & C) = A & (B v C) (A v B) & (A v C) = A v (B & C)

Рассмотрим в качестве примера применения законов ло­гики и правил алгебры логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:

(А &. В) v (A & В).

Воспользуемся правилом дистрибутивности и вынесем за скобки А:

(А & В) v (А & В) = А & (В v В).

По закону исключенного третьего В vВ = 1, следователь­но:

А & (В v B) = А &. 1 = А.

23)

24.1. Позиционные и непозиционные системы счисления. Правила перевода чисел из десятичной системы счисления в n-ричные системы исчисления и обратно.
Существуют позиционные и непозиционные системы счисления. Система счисления - это совокупность численных знаков и правил их записи, которая используется для однозначной записи чисел.
В позиционных системах счисления один и то же символ, в отличие от нспозиционных систем обозначает разные числа, в зависимости от своей позиции относительно остальных.
В нспозиционных системах счисления символ не меняет своего значения в зависимости от своего положения относительно остальных.
Любая позиционная система счисления характеризуется основанием. Основание (базис) позиционной системы счисления - число знаков или символов, использующееся в данной системе.
Для позиционной системы счисления справедливо равенство:
A(4)=aniq" +... + aiq + aoq + aiq +... + a-mq (1) где Ащ»- произвольное число записанное в системе счисления с основанием q; a - цифры системы счисления; m, n - число дробных и целых разрядов.
Пример: значение двойного числа 1001,.1101 можно определить так 1001, 1101(2) = 1х23 + 0x2"' + 0x2° + 1x2*' + 1х2'2 + 0x2° + 1x2"* = 9.8125(ю)
В таблице приведены эквиваленты десятичных цифр в системах счисления
q=10 0 1 2 3 4 5 6 7 8 9 10 И 12 13 14 15
4=2 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111
q=8 0 1 2 3 4 5 6 7 10 И 12 13 14 15 16 17
q=16 0 1 2 3 4 5 6 7 8 9 А В С D Е F
Использование двоичной системы счисления для ЭВМ связано с преодолением трудностей, вызванных необходимостью перевода чисел в двоичную систему счисления и обратно.
Для осуществления перевода целых чисел и целых частей неправильных дробей из систем счисления с основанием qi в новую систему счисления с основанием q2 используется метод, базирующийся на делении переводимого числа на основание новой системы счисления.
В соответствии с (1) целое число А(Чо в системе с основанием q: записывается в виде:
А«»2> = bn iq2 + bn-2q2 +... + biq2 + boq2 = (... (((bn-iq: + b»-2)q2 ■+ Ь*з)ф +... + bi)q2 + bo) (2)
Представление числа А<42) в виде (2) позволяет уяснить суть метода. Если правую часть выражения (2) разделить на величину цз, то можно получить целую часть (...(bniq2 + b«-2) q2 +... + bi) и остаток bo. Повторяя процесс деления п раз, получим последнее частное bn-i которое является старшей цифрой n-разрядного числа с основанием q.
1.1.Чтобы перевести целое число из десятичной системы счисления в систему счисления с основанием необходимо последовательно делить целую часть данного числа на п и записать полученные остатки в обратном порядке.
1.2. Чтобы перевести дробное число из десятичной системы счисления в систему счисления с основанием и необходимо последовательно умножать дробную часть данного числа на п и записать полученные целые части в прямом порядке.
При переводе все арифметические действия вычисляются по правилам системы счисления с основанием qi
Пример: Перевести десятичное число А=98 в двоичную систему счисления
98/2_
98(49 L2_
0 48 [24
1 24 2
0 12I 6 /2_
0 6 [3
0 2
1
Ответ: 98г -► 1100010:
_6_l3~l2_
0 2(1
Для перевода правильных дробей из системы счисления с основанием ql в систему с основанием q2 используется метод базирующийся на основание q2 новой системы счисления. Правильную дробь A(ql) в системе с основанием q2 можно записать в виде:
А(Ч2) = biq2 4- biqi +... b-m q2
Пример: перевести дробь А=0.625 из десятичной в двоичную систему счисления
0 2
b.i=1 250 2
Ь-2=0 500 2
b-3=1 000 2
000
А(2) = 0.1010
Правила выполнения арифметических операции над числами, принятые в десятеричной системе счисления, верны и для других систем. Например, в двоичной системе счисления они имеют вид
♦I 01 х I 01 И01 0 / 0 1 0 I 00 0 101
11110 1101 1110
2. Запись как структурированный тип данных в языке Pascal. Способы описания записей.
Запись - наиболее общий и гибкий структурированный тип в Pascal. Запись представляет собой совокупность ограниченного числа логически связанных компонент, принадлежащих к разным типам. Компоненты записи называются полями, каждое из которых определяется именем. Поле записи содержит имя поля, вслед за которым через двоеточие указывается тип этого поля. Поля записи могут относиться к любому типу, допустимому в языке Паскаль, за исключением файлового типа.
Описание записи в языке Pascal осуществляется с помощью служебного слова RECORD, вслед за которым описываются компоненты записи. Завершается описание записи служебным словом END.
Например, записная книжка содержит фамилии, инициалы и номера телефона, поэтому отдельную строку в записной книжке удобно представить в виде следующей записи: type Row=Record FIO: String[20]; TEL: String[7] end;
var str: Row;
Описание записей возможно и без использования имени типа, например:
var str: Record
FIO: String[20]; TEL: String[7] end;
Обращение к записи в целом допускается только в операторах присваивания, где слева и справа от знака присваивания используются имена записей одинакового типа. Во всех остальных случаях оперируют отдельными полями записей. Чтобы обратиться к отдельной компоненте записи, необходимо задать имя записи и через точку указать имя нужного поля, например:
str.FIO, str.TEL
Такое имя называется составным. Компонентой записи может быть также запись, в таком случае составное имя будет содержать не два, а большее количество имен.
Обращение к компонентам записей можно упростить, если воспользоваться оператором присоединения with.
Он позволяет заменить составные имена, характеризующие каждое поле, просто на имена полей, а имя записи определить в операторе присоединения:
with M do OP;
Здесь М - имя записи, ОР - оператор, простой или составной. Оператор ОР представляет собой область действия оператора присоединения, в пределах которой можно не использовать составные имена.
Pascal допускает вложение записей друг в друга, т.е. поле записи может также быть записью.

25)Арифметические операции в позиционных системах счисления

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам.

Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания.

Сложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 1102 и 112:

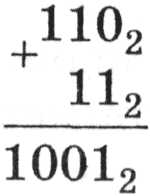
Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим:

1102 = 1 × 22 + 1 × 21 + 0 × 20 = 610;

112 = 1 × 21 + 1 × 20 = 310;

610 + 310 = 910.

Теперь переведем результат двоичного сложения в десятичное число:

10012 = 1 × 23 + 0 × 22 + 0 × 21 + 1 × 20 = 910.

Сравним результаты - сложение выполнено правильно.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:

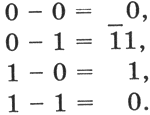
Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов из старших разрядов. В качестве примера произведем вычитание двоичных чисел 1102 и 112:

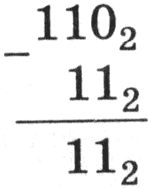
Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:

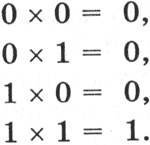
Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на цифры множителя. В качестве примера произведем умножение двоичных чисел 1102 и 112:

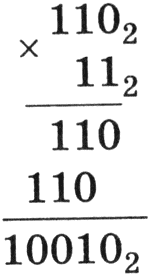
Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 1102 на 112:

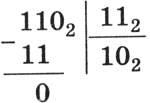
Арифметические операции в восьмеричной и шестнадцатеричной системах счисления. Аналогично можно выполнять арифметические действия в восьмеричной и шестнадцатерич-ной системах счисления. Необходимо только помнить, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления:

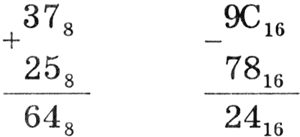
Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.

Дата добавления: 2015-04-24