
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для любой функции алгебры логики существует своя СДНФ, причем единственная
|
|
|
|
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности статьи Минимизация логических функций методом Квайна, в которой нахождение СДНФ встречается несколько раз:

| 
| 
| 
| 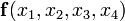
|
В ячейках строки́ 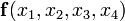 отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы.
отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы.
Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
Первый столбец содержит 1 в указанном поле. Отмечаются значения всех четырёх переменных, это:
-
 = 0
= 0 -
 = 0
= 0 -
 = 0
= 0 -
 = 0 12
= 0 12
Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: 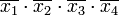
Переменные второго члена:
-
 = 0
= 0 -
 = 0
= 0 -
 = 0
= 0 -
 = 1
= 1
 в этом случае будет представлен без инверсии:
в этом случае будет представлен без инверсии: 
Таким образом анализируются все ячейки 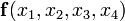 . Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
Совершенная ДНФ этой функции:
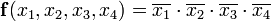







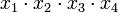
СКНФ (Совершенная Конъюнктивная Нормальная Форма) — это такая КНФ, которая удовлетворяет трём условиям:
· в ней нет одинаковых элементарных дизъюнкций
· в каждой дизъюнкции нет одинаковых пропозициональных букв
· каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
[править] Пример нахождения СКНФ
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности статьи Минимизация логических функций методом Квайна:

| ||||||||||||||||

| ||||||||||||||||

| ||||||||||||||||

| ||||||||||||||||
|
В ячейках строки́ 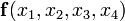 отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.
отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.
Четвертый столбец содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:
·  = 0
= 0  = 0
= 0  = 1
= 1  = 1
= 1
В дизъюнкцию записывается переменная без инверсии если она в наборе равна 0 и с инверсией если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так: 
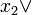
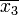


Остальные члены СКНФ составляются по аналогии.
Полином Жегалкина — полином(многочлен) над Z 2, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берется конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве удобного средства для представления функций булевой логики.
Полином Жегалкина представляет собой сумму по модулю два (операция Исключающее ИЛИ) произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде

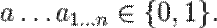
или в более формалиизованном виде как
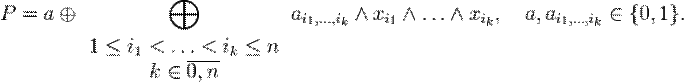
Примеры полиномов Жегалкина:
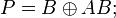


По теореме Жегалкина каждая булева функция единственным образом представляется в виде полинома Жегалкина. Теорема доказывается следующим образом. Заметим, что различных булевых функций от n переменных 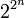 штук. При этом конъюнкций вида
штук. При этом конъюнкций вида 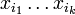 существует ровно 2n, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует
существует ровно 2n, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует 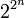 различных полиномов Жегалкина от n переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.
различных полиномов Жегалкина от n переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.
Полнота и замкнутость системы.
Определение полноты системы функций в k- значной логике аналогично соот-
ветствующему определению в двузначной логике.
Определение. Система функций f  , …, f
, …, f 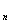 из P
из P  называется (функционально)
называется (функционально)
полной, если любая функция из P  может быть записана в виде формулы через функ-ции этой системы.
может быть записана в виде формулы через функ-ции этой системы.
Для обоснования полноты системы функций в k – значной логике можно так же
использовать принцип сведения задачи о полноте других систем, 14
Приведем некоторые примеры полных систем в k – значной логике.
1. Множество всех функций из P  является полной системой.
является полной системой.
2.Система Россера-Туркетта: {0, 1, …, k-1, J 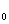 (x),…, J
(x),…, J 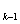 (x), min(x,y), max(x,y)} – полная система в P
(x), min(x,y), max(x,y)} – полная система в P  . Действительно, для произвольной функции из P
. Действительно, для произвольной функции из P  справедливо равенство, правая часть которого состоит из функций данной системы, т.е. любая функция из P
справедливо равенство, правая часть которого состоит из функций данной системы, т.е. любая функция из P  выражается через эти функции
выражается через эти функции
3. Система Поста: { 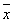 , max (x,y) } является полной.
, max (x,y) } является полной.
4. Система: { V  (x,y) } – полная. Вопрос о ее полноте может быть легко све-
(x,y) } – полная. Вопрос о ее полноте может быть легко све-
ден к полноте системы 3.
В k – значных логиках исследование произвольной системы функций на полноту сопряжено с большими техническими трудностями: использование критерия полноты, основанного на рассмотрении всех предполных классов в P  , даже при k = 3 и 4 требует проверки весьма значительного числа условий т.к. в P
, даже при k = 3 и 4 требует проверки весьма значительного числа условий т.к. в P  существует ровно 18, а в P
существует ровно 18, а в P 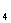 – ровно 82 предполных классов.
– ровно 82 предполных классов.
Доказательство полноты конкретных систем в P  проводится обычно методом сведения к заведомо полным системам. С понятием полноты связано понятие замыкания и замкнутого класса, определения которых аналогичны соответственным определениям для двузначной логики.
проводится обычно методом сведения к заведомо полным системам. С понятием полноты связано понятие замыкания и замкнутого класса, определения которых аналогичны соответственным определениям для двузначной логики.
Приведем примеры замкнутых классов.
1. Класс P  , очевидно, является замкнутым.
, очевидно, является замкнутым.
2. Пусть e  E
E  . Обозначим через T
. Обозначим через T  множество всех функций f (x
множество всех функций f (x  , …, x
, …, x 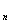 )
)
из P  сохраняющих e, т.е. таких, что f (a
сохраняющих e, т.е. таких, что f (a  , …, a
, …, a 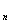 )
)  e, если a
e, если a 
 e, (i = 1, …, n). Класс T
e, (i = 1, …, n). Класс T  очевидно, является замкнутым.
очевидно, является замкнутым.
3. Множество всех линейных функций из P  образует замкнутый класс линей-
образует замкнутый класс линей-
ных функций, который обозначается через L  (или L). Этот класс отличен от P
(или L). Этот класс отличен от P  при любом k > 2.
при любом k > 2.
4. Множество всех функций из P  , представимых полиномами по модулю k,
, представимых полиномами по модулю k,
является замкнутым классом в P  .
.
Понятие замкнутого класса может быть приложено к решению вопроса об обос-новании неполноты некоторых систем.
Теорема Поста о полноте. По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали
1. Хотя бы одна функция, не сохраняющая 0;
2. Хотя бы одна функция, не сохраняющая 1;
3. Хотя бы одна нелинейная функция;
4. Хотя бы одна немонотонная функция;
5. Хотя бы одна несамодвойственная функция.
Исходя из этого, система функций  является полной, так как в ней:
является полной, так как в ней:
1) Не сохраняет 0: 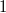 ; 2) Не сохраняет 1:
; 2) Не сохраняет 1:  ; 3) Нелинейна:
; 3) Нелинейна:  ; 4) Немонотонна:
; 4) Немонотонна:  ; 5) Несамодвойственны:
; 5) Несамодвойственны: 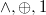 .
.
На основе этой системы и строятся полиномы Жегалкина. 15
Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа, отождествив его вершины с частями города, а ребра — с мостами, которыми связаны эти части.
Эйлеру удалось доказать, что искомого маршрута обхода города не существует.
Неориентированным графомG (V, E) называется совокупность двух множеств: не пустого множества V ( множества вершин) и множества E - множество неупорядочных пар элементов из V (множества ребер).
Пусть v и u вершины графа, e = (v, u) это ребро графа, тогда вершина v и ребро e u называются инцидентными, вершина u и ребро e так же инцидентные.
Два ребра инцидентные одной вершине называются смежными.
Две вершины инциденты одному ребру называются смежными.
Степенью или валентностью вершины называется количество ребер инцидентности этой вершины d (V).
Минимальная степень графа 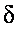 (G). Максимальная степень графа
(G). Максимальная степень графа 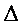 (G).
(G).
Регулярным графом степени k называется граф, степени всех вершин равны k.
Вершина называется изолированной, если ее степень равна 0.
Вершина называется висячей, если ее степень равна 1.
Петлей называется ребро, начинающееся и заканчивающееся в одной вершине.
Кратными ребрами называется ребра инцидентные одной и той же паре вершин.
Простым графом называется граф без петель и кратных ребер с конечным количеством вершин.
Граф называется полным, если любая пара вершин соединена одним ребром.
Маршрутом в графе называется последовательн вершин и ребер v 0 v 1 v 2 v 3 … v n.
Длиной маршрута называется количества ребер в нем.
Маршрут, в котором все вершины различны, называется простой цепью.
Замкнутая простая цепь называется простым циклом.
Замкнутая цепь называется циклом.
Расстоянием между вершинами u и v называется длина кратчайшей цепи d (u, v).
Кратчайшая цепь, соединяющая вершины называется геодезическая.
Диаметром графа G называется длина длиннейшей геодезической цепи.
Орграф! При описании с помощью графов различных сетей, алгоритмов и т. п. часто необходимо учитывать не только то, какие точки соединены, но и в каком направлении.
Ориентированный граф или орграф называется граф, у которого множество ребер является множеством упорядочных пар. Началом ребра называется вершина, указанная в паре первой, концом – вторая вершина этой пары (графически она указана стрелкой). Ребра при изображении ориентированных графов представляют стрелками. Ребро ориентированного графа называется дугой. Если вершины u и v определяют дугу, то вершина u называется антицидентом вершины v.
Степенью входа (выхода) вершины орграфа называется число ребер, для которых эта вершина является концом (началом). Будем обозначать соответственно эти степени для некоторой вершины v  и
и  .
.
Дуги орграфа называются кратными, если они имеют одинаковые начальные и конечные вершины, то есть одинаковые направления Путемv 0 v 1… v n, где vi антицендент vi+1 .. Контуром в ориентированном графе называют путь начинающейся и заканчивающейся в одной вершине. Граф, в котором нет контура, назыв безконтурным 16
Графы. Способы задания. Матрица смежности. Матрица инцидентности.
Способы задания графа
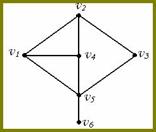
1 Явное задание графа как алгебраической системы.
<{ a,b,c,d },{ u,v,w,x }; {(u,a),(u,b),(v,b),(v,c),(w,c),(w,a),(x,c), (x,d)}>. Так как мы рассматриваем только простые графы, граф нам проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин
2 Геометрический способ
3 Задание графов матрицей смежности:
Матрица смежности – это квадратная матрица порядка p (количество вершин), элемент которой, стоящий в i строке и j столбце определяется по правилу:

ПРИМЕР

2. Задание графов матрицей инцидентций.
Матрицей инцидентции называется прямоугольная матрица размерности 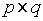 (p – количество вершин, q – количество ребер), элемент которой стоящий в i строке и j столбце определяется по правилу:
(p – количество вершин, q – количество ребер), элемент которой стоящий в i строке и j столбце определяется по правилу:

- для неориентированного графа.

- для ориентированного графа.
Понятие изоморфизма для графов имеет наглядное толкование. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей.
 Пример 1 (изоморфизм). Покажем, что следующие два графа изоморфны. Действительно, отображение a ® e, b ® f, c ® g, d ® h, являющееся изоморфизмом легко представить как модификацию первого графа, передвигающую вершину d в центр рисунка. 17
Пример 1 (изоморфизм). Покажем, что следующие два графа изоморфны. Действительно, отображение a ® e, b ® f, c ® g, d ® h, являющееся изоморфизмом легко представить как модификацию первого графа, передвигающую вершину d в центр рисунка. 17
Дерево решен. Остовное дерево. Жадный алгоритм. Алгоритм ближайшего соседа.
Возможности выбора при решении проблемы можно представить в виде ориентированного дерева, где в корне – проблема, дуге соответствует один из вариантов выбора, вершине - новая ситуация, возникающая в результате реализации приписанного дуге варианта. Такой трактовке соответствует граф типа дерева, получивший название «дерево решений». Предположим, что можно оценить эффективность принятого выбора. Тогда возникает задача поиска среди возможных путей от корня (когда проблема поставлена) к одному из листьев (когда проблема решена) пути, имеющего оптимальную оценку.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 988; Нарушение авторских прав?; Мы поможем в написании вашей работы!