Явление электромагнитной индукции. Опыты Фарадея. Закон Фарадея и правило ленца

Т. е. работа по перемещению проводника с током в магнитном поле равна произведе­нию силы тока на магнитный поток, пересеченный движущимся проводником. Получен­ная формула справедлива и для произвольного направления вектора В.

Для определения этой работы рассмотрим проводник длиной l с током I (он может свободно перемещаться), помещенный в однородное внешнее магнитное поле, перпен­дикулярное плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна

Работа по перемещению проводника и контура с током в магнитном поле

На проводник с током в магнитном поле действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки, рис. 177), то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током.

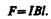
Под действием этой силы проводник переместится параллельно самому себе на отрезок d x из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

так как l d x= d S — площадь, пересекаемая проводником при его перемещении в маг­нитном поле, B d S= dФ — поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,

(121.1)

Вычислим работу по перемещению замкнутого контура с постоянным то­ком I в магнитном поле. Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение М', изоб­раженное на рис. 178 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж) указано на рисунке. Контур М мысленно разобьем на два соединенных своими концами проводника: AВС и CDА.

Работа d A, совершаемая силами Ампера при рассматриваемом перемещении кон­тура в магнитном поле, равна алгебраической сумме работ по перемещению провод­ников AВС (d A ₁) и CDA (d A ₂), т. е. (121.2)

Силы, приложенные к участку CDA контура, образуют с направлением перемеще­ния острые углы, поэтому совершаемая ими работа dA ₂ > 0.. Согласно (121.1), эта работа равна произведению силы тока I в контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ₂, пронизывающий контур в его конеч­ном положении. Следовательно, 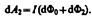(121.3)

Силы, действующие на участок AВС контура, образуют с направлением перемеще­ния тупые углы, поэтому совершаемая ими работа d A ₁<0. Проводник AВС пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ₁, пронизывающий контур в начальном положении. Следовательно, (121.4)

Подставляя (121.3) и (121.4) в (121.2), получим выражение для элементарной работы:

где dФ₂ — dФ₁ = dФ ' — изменение магнитного потока сквозь площадь, ограниченную контуром с током. Таким образом, (121.5)

Проинтегрировав выражение (121.5), определим работу, совершаемую силами Ампера, при конечном произвольном.перемещении контура в магнитном поле: (121.6)

т. е. работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Формула (121.6) остается справедливой для контура любой формы в про­извольном магнитном поле. Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле 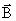, перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор 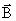сонаправлен с .

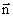На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: 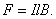Пусть проводник l переместится параллельно самому себе на расстояние d x. При этом совершится работа:

Итак, (2.9.1) Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции. Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле. Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток 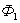, пронизывающий контур, направлен по нормали 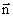к контуру, поэтому .

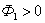Рис. 2.18

Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком . Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком . Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура: где 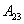, равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку). 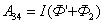Провод 1–2 перерезает поток (), но движется против сил действия магнитного поля. Тогда общая работа по перемещению контура 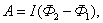или 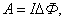(2.9.2) здесь – это изменение магнитного потока, сцепленного с контуром. Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром. Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле (2.9.5) Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины d Ф различен. Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется 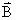, то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу

Эта фундаментальная задача была блестяще решена в 1831 г. английским физиком М. Фарадеем, открывшим явление электромаг­нитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Рассмотрим классические опыты Фарадея, с помощью которых было обнаружено явление электромагнитной индукции.

Опыт I (рис. 179, а). Если в замкнутый на гальванометр соленоид вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрелки гальванометра (возникает индукционный ток); направления отклонений стрелки при вдвигании и выдвигании магнита противоположны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При изменении полюсов магнита направление отклонения стрелки изменится. Для получения индукционного тока магнит можно оставлять неподвижным, тогда нужно относительно магнита передвигать соленоид.

Опыт П. Концы одной из катушек, вставленных одна в другую, присоединяются к галь­ванометру, а через другую катушку пропускается ток. Отклонение стрелки гальванометра наблю­дается в моменты включения или выключения тока, в моменты его увеличения или уменьшения или при перемещении катушек друг относительно друга (рис. 179, б). Направления отклонений стрелки гальванометра также противоположны при включении или выключении тока, его увеличе­нии или уменьшении, сближении или удалении катушек.

Опытным путем было также установлено, что значение индукционного тока совер­шенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения (в опытах Фарадея также доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше скорость движения маг­нита, или скорость изменения силы тока, или скорость движения катушек).

Закон фарадея. Обобщая результаты своих многочисленных опытов, Фарадей пришел к количествен­ному закону электромагнитной индукции. Он показал, что всякий раз, когда проис­ходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электро­магнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электро­магнитной индукции определяются только скоростью изменения магнитного потока, т. е.

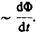
Теперь необходимо выяснить знак . В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта (см. § 109). Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к форм­улировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим кон­туром, возникающая в контуре э. д. с.

(123.2)

Знак минус показывает, что увеличение потока вызывает э. д. с. т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока вызывает т.е. направления потока и поля индукционного тока совпадают. Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызва­вшему этот индукционный ток Закон Фарадея можно сформулировать еще таким образом: э.д.с. 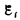электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э. д. с. не зависит от способа изменения магнитного потока. Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

Дата добавления: 2015-04-24