Статистические ряды

Статистический ряд распределения – это упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он, являясь разновидностью структурной группировки, характеризует состав (или структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.

Ряды распределения, построенные по атрибутивному признаку, называются атрибутивными (распределение населения по полу, занятости, профессии и т.д.).

Ряды, построенные по количественному признаку вариационными (распределение населения по стажу работы, з/п, возрасту.).

В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды распределения.

В дискретном вариационном ряде распределения группы составлены по признаку, изменяющемуся дискретно и принимающему только целые значения.

В интервальном вариационном ряде распределения группировочный признак, составляющий основание группировки, может принимать в определенном интервале любые значения.

Для анализа совокупности вариационный ряд дополняют такими элементами, как накопленная частота, накопленная частость и плотность распределения.

Вариантой называют отдельное значение варьируемого признака, которое он принимает в ряду распределения.

Частота – это численность отдельных вариант или каждой группы вариационного ряда.

Частости – это частоты, выраженные в виде относительных величин: долях единицы или в процентах, рассчитываются как отношение частоты к объему совокупности. Сумма частостей всегда равна единице или 100 %. Замена частот частостями позволяет сопоставлять вариационные ряды с разным числом наблюдений.

Накопленная частота (Sf)показывает число единиц совокупности, у которых значение варианты не больше данной, определяется суммированием частот всех предшествующих интервалов, включая данный:

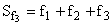, , и т.д.

Если вместо частот использовать частости, то аналогично получим накопленные частости(Sw):

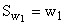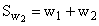, , и т.д.

Плотность распределения – это отношение числа единиц совокупности к ширине интервала.

Абсолютная плотность распределения – это частота, приходящаяся на единицу длины интервала,
Относительная плотность распределения – частость, приходящаяся на единицу длины интервала,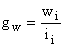

Графически ряды распределения можно представить в виде гистограммы, кумуляты, полигона.

Интервальный вариационный ряд изображают в виде гистограммы. Для ее построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, равные длине интервала. Затем на этих отрезках, как на основаниях, строят прямоугольники, высота которых пропорциональна частоте или частости. Для интервального ряда с неравными интервалами по оси ординат откладывают плотность распределения, так как в этом случае

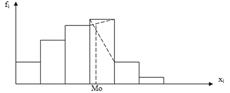
именно она дает представление о заполненности интервала. Площадь всей гистограммы численно равна сумме частот.

Если соединить середины каждого интервала отрезками прямой, то получим замкнутую фигуру в виде многоугольника, которая называется полигоном. Полигон чаще используется для дискретных рядов. Для этого в прямоугольной системе координат строят точки с координатами (x1, f1), (x2, f2), …, (xN, fN), затем последовательно соединяют их отрезками, а из первой и последней точек опускают перпендикуляры на ось х. Полученный многоугольник является полигоном дискретного вариационного ряда.

Кумулята строится по накопленным частотам (или частостям), которые

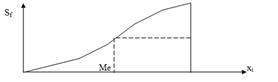
откладывают по оси у, а по оси х – варианты или верхние границы интервалов.

Дата добавления: 2015-04-24