Статистика носіїв заряду в напівпровідниках

Статистика носіїв заряду в н/п

У класичній механіці потрібно мати три складові. якщо є 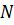частинок і потрібно знайти середнє значення. відхилення від середнього значення

(ф1)

якщо число частинок є велике то середнє рівне .

(ф2)

Відхилення від середньої густини

(ф3)

величина настільки мала що можна вважати що частинки рівномірно розподілені по кристалу.

Розподіл частинок за енергіями в кристалі. Воно буде визначатися повною статистичною функцією розподілу і буде задаватися двома параметрами

(ф4)

від є це функція, яка надає нам ймовірність заповнення енергетичних станів. Якщо рівень фермі розташований нижче дна зони провідності так що величина є мінус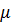

(ф5)

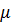це рівень фермі в напівпровіднику.

(ф6)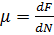

Це та енергія на величину якої зміниться вільна енергія при зміні числа частинок на одиницю.

приведений рівень хімічного потенціалу або рівень фермі.

Рівень фермі характеризує енергетичний стан електронів в кристалі. Електронний газ може бути вироджений або не вироджений.

(ф7)

Якщо у не виродженому напівпровіднику рівень фермі є в забороненій зоні, якщо є мінус 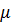є набагато більше за то функція Фермі-Дірака

(ф8)

в такому випадку можна дати означення виродженості електронного газу виходячи з функції Фермі-Дірака то електронний газ в кристалі буде не виродженим в такому випадку повну статистичну функцію розподілу:

(ф9)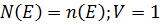

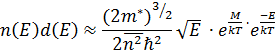
задає ймовірність розподілу частинок за енергіями При те прямуючому до 0 градусів то еф від є буде рівне 1 якщо є менше за .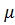

Всі енергетичні стани які є нижче рівня фермі є заняті електронами підвищення температури електрони переходять на вищі енергетичні рівні і міняється 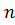від є

(ф10)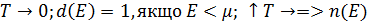

Рівень Фермі при збільшенні температури буде розмиватись дуже слабо.

Для всіх значень енергії які більші за рівень Фермі

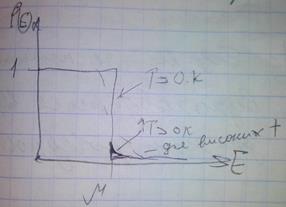
Рис 1. При т прямуючому до 0.

(ф11)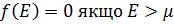

чим вища температура то хвіст теж буде більший.

Функція густини станів дозволені хвильові значення хвильового вектора 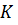співпадають в кожній енергетичній зоні для пружно деформованих хвиль то функція густини станів може бути рівна густині мод за чистотою в деформованому кристалі. а число дозволених значень вектора .

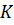(ф12)

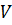об’єм і якщо врахувати, що електрон має два спіни то густина станів запишеться

(ф13)

у випадку величини енергії електрона на електрона на першій орбіті

(ф14)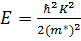

звідси ефективна маса дорівнює

(ф15)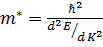

якщо вказати ці всі величини то функцію 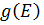від є можна записати.

(ф16)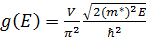

Якщо мова йде про розподіл електронів то системою відліку буде дно зон провідності. Отже повна концентрація електронів це є інтеграл

(ф17)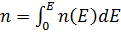

густина станів у валентній зоні та зоні провідності

Рис 2.

Якщо проінтергувати (17) то ми получимо Больцманівський розподіл можна дістати повне число частинок в енергетичній зоні не виродженого електронного газу пропорційне величині а розподіл цих частнок за енергіями записується наступним чином:

(ф18)

для не виродженого напівпровідника функція енергетичних станів завжди буде йти нижче.

Рис 3.

При великих енергіях 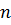від є може досягати максимуму,

отже для не виродженого електронного газу повне число електронів задається величиною електрохімічного потенціалу буде виражене формулою.

(ф19)

Дана функція дає нам число електронів в зоні.

спрощений вираз

(ф20)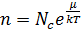

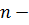це ефективне число станів приведене до дна зони провідності.

Міркування для розрахунку дірок є аналогічні ж урахуванням того, що

(ф21)

для дірок отримаємо вираз

(ф22)

тепер

(ф23)

а ефективна густина станів приведена до стелі валентної зони.

За допомогою цих виразів можна знайти положення рівнів фермі в будь якому напівпровіднику.

Якщо Т величини концентрацій

(ф24)

якщо прирівняти ці дві величини то за умови відсутності легування якщо 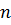рівне то такий напівпровідник називається власним напівпровідником.

(ф25)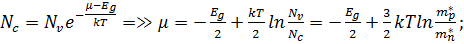

Рівень Фермі зміщується туди де менша ефективна маса.

Можна стверджувати при Т прямуючому до 0 К рівень Фермі буде строго по середині забороненої зони.

З підвищенням температури рівень Фермі буде зміщуватися до тієї зони де менша густина енергетичних станів.

Оскільки ефективна маса електрона і дірки може бути однакова то вище викладені міркування є справедливі для вузько зонних напівпровідників тобто 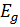менше 1. Власний напівпровідник будемо позначати 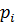або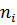

(ф26)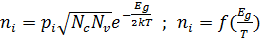

Рівноважна концентрація носіїв струму в напівпровіднику визначається двома параметрами 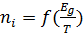температури.

У реальних напівпровідниках

(ф27)

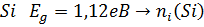
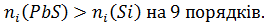
для прикладу можна взяти кремній при кімнатній температурі Т=1000 градусів і порівняємо його. При кімнатній температурі в менша на 11 порядків.

Маючи значення концентрації носіїв заряду можна визначити експерементально і розрахунково ширину забороненої зони. Даний метод визначення забороненої зони є придатний для широкозонних напівпровідників.

Дата добавления: 2015-05-08