Билет 2. 3. Коллективный выбор. Из многочисленных задач выбора особый практический интерес представляет задача многостороннего принятия решения

3. Коллективный выбор. Из многочисленных задач выбора особый практический интерес представляет задача многостороннего принятия решения, когда выбор осуществляется не одним лицом, а группой лиц. При этом предполагается высшая степень согласия между членами группы относительно общей цели, выбор же приходится делать между вариантами средств достижения этой цели. Типичным примером являются выборы на руководящий пост. Такую операцию называют процедурой голосования.

Семь парадоксов голосования:

- коллектив не всегда прав: коллектив состоит из субъектов, каждый из которых может заблуждаться;

- возможность непринятия решения: любая процедура голосования может закончиться тем, что согласованные условия принятия решения не будут выполнены (например, голоса разделятся поровну) и, следовательно, решение не будет принято;

- парадокс Кондорсе. Суть парадокса в возможности цикличности графа предпочтений. Например, пусть каждая из трех фракций парламента, образующих большинство лишь попарно, выдвинула свой вариант законопроекта: a, b и с. Если у этой троицы индивидуальные предпочтения таковы: (а>b>с), (b>с>а) и (с>а>b), то они попали в парадокс Кондорсе;

- возможность победы меньшинства при мажоритарной системе голосования:

а) признание легитимными (законными) выборы при низкой (меньше 50%) явке избирателей. Решение автоматически предоставляется меньшинству;

б) "растаскивание" голосов. Пусть одна коалиция обладает 60 % потенциальных голосов, второй принадлежит 40 % электората. Если первые выдвинут двух кандидатов, да еще равноценных, а вторые одного - победит меньшинство;

в) пусть решение принимается большинством голосов в 2/3. Если в итоге победил представитель меньшинства, значит, на последнем этапе процедуры он набрал большинство. Если же участников последнего этапа голосования самих выбирали по тому же правилу, то возможна следующая ситуация:

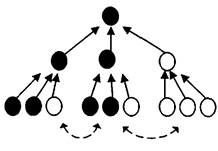
Легко видеть, что победило меньшинство в 4/9 против 5/9. Для реализации такой возможности необходимо выполнение трех условий: выборы должны быть многоступенчатыми, меньшинство должно соблюдать дисциплину голосования, меньшинство должно быть достаточно многочисленным для обеспечения своего большинства на последнем этапе;

- парадокс подавляющего большинства: какой бы высокий процент большинства ни был назначен для легитимности принятия решения, решение не является демократическим. Данная процедура узаконивает принесение в жертву интересов одного всем остальным, а суть демократии состоит в том, чтобы на этапе исполнения решения были защищены интересы любого меньшинства, и прежде всего - основные права каждой отдельной личности;

- парадоксы единогласия. Если определить демократию как защиту интересов каждого, то единственной демократической процедурой голосования оказывается единогласное принятие решений. Однако и в этом случае возникают парадоксальные ситуации:

а) иногда принцип единогласия ("все за") подменяется принципом консенсуса ("никто не против"), тогда как это разные вещи: воздержавшиеся отождествляются с согласными, отсутствующие исключаются из принимаемых во внимание;

б) желательное решение никак не может набрать 100 % голосов. Существует по крайней мере два способа попытаться достичь согласия в такой ситуации: поиск компромисса, либо "способом лестницы" (можно попытаться подойти к желаемой, но никак сразу не достигаемой единогласно цели, мелкими шагами, каждый из которых реализуется единогласно);

- теорема Эрроу о невозможности. Требования «правильного» коллективного выбора по Эрроу:

а) все индивидуальные предпочтения должны как-то быть учтены; не должно быть такого индивида, чье мнение принимается обязательным для всех, независимо от мнения остальных (нежелательность диктаторства);

б) если в результате группового выбора предпочтение было отдано какой-то альтернативе, то это решение не должно меняться, если кто-нибудь из ранее отвергавших ее изменил свое мнение в ее пользу (условие монотонности).

в) если изменения индивидуальных предпочтений не коснулись каких-то альтернатив, то в новом групповом упорядочении порядок этих альтернатив не должен измениться (условие независимости альтернатив);

г) для любой пары альтернатив возможны такие два множества индивидуальных предпочтений, при которых порядок этих альтернатив противоположен ("условие суверенности").

Однако, указанные требования несовместны, т.е. не существует процедур голосования, удовлетворяющих всем этим требованиям. Причиной такого результата являются упомянутые выше парадоксы.

Дата добавления: 2015-05-08