Часть 1. Динамика движения тела по окружности: выпуклый и вогнутый мост, «мертвая петля», конический маятник, тело на вращающемся диске

Динамика движения тела по окружности: выпуклый и вогнутый мост, «мертвая петля».

При равномерном движении тела по окружности используется формула,

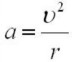,где u- скорость автомобиля; r- радиус кривизны.

Следует учесть, что в условиях нашего рельефа местности дороги имеют огромное количество подъемов и спусков, поворотов, а это ничто иное, как движение по части окружности.

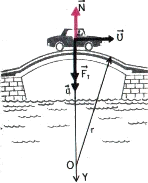Автомобиль, движущийся по выпуклому мосту легче того же автомобиля, неподвижно стоящего на том же мосту.

Действительно, движение по выпуклому мосту – это движение по части окружности. Поэтому автомобиль движется с центростремительным ускорением, равным по модулю:

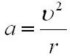, где u- скорость автомобиля; r- радиус кривизны.

В момент, когда автомобиль находится в высшей точке моста, это ускорение направлено по вертикали вниз. Оно сообщается автомобилю равнодействующей силы тяжести

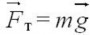и силы реакции моста.

Уравнение, выражающее второй закон Ньютона в векторной форме, запишется так:

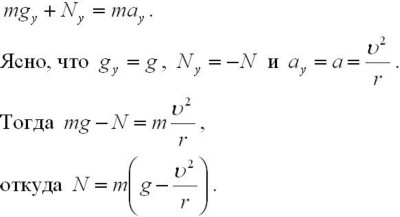
Вес автомобиля 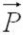(сила, с которой он давит на мост) по третьему закону Ньютона направлен противоположно силе реакции моста , а по модулю эти сил равны, следовательно,

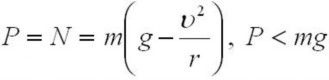
Обратите внимание, что при некоторой минимальной скорости

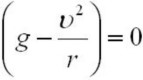, когда 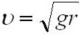автомобиль потеряет опору, а значит и управление, - он взлетает!

Аналогично можно показать уменьшение веса пассажиров, едущих в автомобиле по выпуклому мосту.

Случай, когда кривизна моста направлена вниз, рассматривается аналогично.

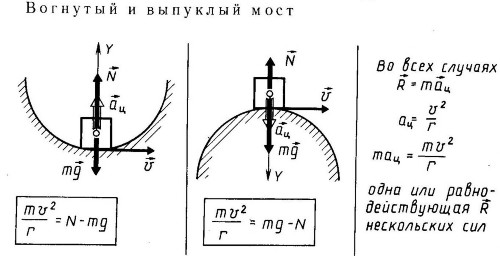
Тогда вес транспортного средства можно найти так:

А еще встречаются случаи:

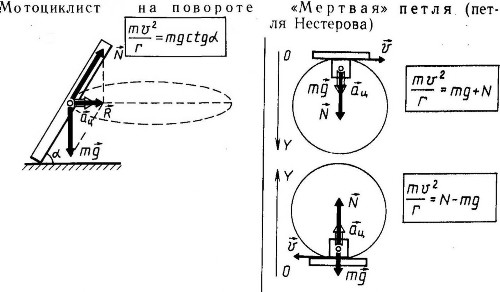
Конический маятник.

Конический маятник. В коническом маятнике (рис.61) тело маятника (небольшое по размерам тело) вращается в горизонтальной плоскости. Угол, образуемый нитью подвеса с вертикалью, проведенной через точку подвеса, остается неизменным. Вес маятника G можно разложить на две составляющие: центростремительную силу Z, направленную к центру круга, и силу Q, направленную вдоль нити:

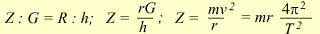
Отсюда получаем:

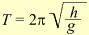
Для малых углов конуса h ≈ l; тогда период колебаний конического маятника

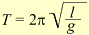
Если спроектировать движение конического маятника на вертикальную плоскость, то тень маятника совершает гармоническое движение (рис.62). Закон

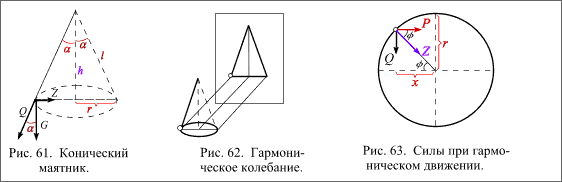
гармонического движения легко получить на основе кругового движения (рис. 63):

P = Z cos φ = Z (x: r) = k x, k = Z: r = const.

Гармоническое движение характеризуется тем, что сила, направленная к положению равновесия, пропорциональна удалению маятника от положения равновесия. В процессе колебаний происходит повторяющееся превращение потенциальной энергии в кинетическую и обратно. В точках поворота скорость равна нулю, в положении равновесия скорость максимальна.

Период гармонического колебания:

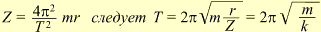
3. Плоский маятник. Математический маятник.

Колебания маятника, подвешенного на нити (рис.64), при малых углах отклонения (не превышающих 5º) можно считать гармоническими:

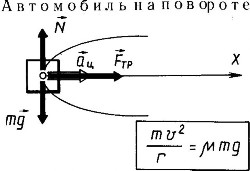
Тело на вращающемся диске.

На расстоянии R от оси горизонтально расположенного диска находится тело, коэффициент трения которого о диск равен k. Диск вращается с угловой скоростью ω.

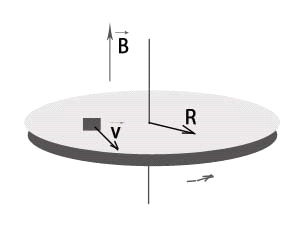
На тело действуют три силы:

сила тяжести mg, сила реакции опоры N и сила трения Nтр.

В инерциальной системе отсчета, связанной с Землей, второй закон Ньютона будет иметь вид:

ma = mg + N + Fтр

Движение тела относительно Земли представляет собой движение в горизонтальной плоскости по окружности радиусом R. Силы, действующие на него в вертикальном направлении, скомпенсированы. Вектор ускорения лежит в горизонтальной плоскости, а само ускорение является центростремительным. Его величина определяется формулой:

aц = ω2R.

Проецирование векторного уравнения на координатные оси X и Y дает два скалярных уравнения:

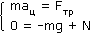
Первое уравнение показывает, что в роли центростремительной силы выступает сила трения, второе — констатирует, что вертикальные силы взаимно уравновешены.

Сила трения покоя подчиняется неравенству:

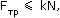поэтому при слишком больших скорости или радиусе вращения сила трения не сможет обеспечить требуемое центростремительное ускорение, и тело начнет соскальзывать.

Преобразуем неравенство:

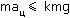
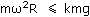
Следовательно, условие отсутствия скольжения:

.

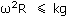Дата добавления: 2015-05-08