Основы теории процесса истечения

Определение скорости и расхода при истечении жидкости через отверстия и насадки

На практике жидкость может вытекать из ёмкостей через отверстия и насадки различных типов.

Рис.23

Схема истечения через отверстие и насадок

Боковые частицы (пунктирные стрелки) по инерции движутся горизонтально и сжимаот ядро струи. На некотором расстоянии от входа в отверстие (насадок) получается сжатое сечение.

w_с / w = e - коэффициент сжатия. e = 0,64 при Re > 10⁴.

В сжатом сечение струи в насадке давление меньше, чем атмосферное р_ат. Жидкость движется в сторону большего давления. Частицы жидкости с малой скоростью (у стенки) поворачивают обратно. Образуются вихри.

При уменьшении давления в сжатом сечении увеличивается скорость движения, следовательно, и расход. Если бы не было насадка (отверстие), давление в струе равно атмосферному, скорость меньше и расход меньше.

При решении задач на истечение жидкости применяются следующие законы:

· закон сохранения расхода: Q = сonst в любом сечении потока.

Для схемы Рис.23 расход через отверстие равен расходу через насадок и равен тому расходу, который поступает в бак.

· закон сохранения энергии: разность потенциальных энергий на входе и выходе из отверстия (насадка) превращается с некоторыми потерями в кинетическую энергию вытекающей струи жидкости.

Потенциальная энергия жидкости равна m×g×z +m× p/r. Поскольку высота отверстия (насадка) незначительна, z»const и разность потенциальных энергий на входе и выходе из отверстия (насадка) равна:

DE_пот =m× p_вх/r - m× p_вых/r = m ×(p_вх – р_вых) /r

Кинетическая энергия струи равна mJ²/2.

Закон сохранения энергии:

j× m ×(p_вх – р_вых) /r = mJ²/2.

Здесь j< 1 – «к.п.д.» процесса, он учитывает, что не вся потенциальная энергия превращается в кинетическую, часть её расходуется на преодоление гидравлических сопротивлений и переходит в тепло.

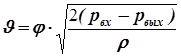(54)

Формула (54) определяет скорость в сжатом сечении струи для отверстия и выходную скорость для насадка.

При истечении через отверстие имееют место потери на входе, а при истечении через насадок – те же потери на входе плюс потери на вихреобразование внутри насадка.

j_нас. < j_отв! j_нас. = 0,82; j_отв = 0,97 – практически при Re >10⁵, когда наступает автомодельность (независимость от числа Re).

При определении расхода нужно умножить скорость на площадь сечения.

;

Здесь m = j×e - коэффициент расхода. Для отверстия [11] m_отв = 0,97×0,64 =0,6.

Для насадка в выходном сечении нет сжатия (Рис.23), e = 1 и m _нас = j_нас = 0,82.

(55)

Итак:

Расход при истечении через отверстие и насадок определяется по одной и той же формуле (55). Разница – в значении коэффициента расхода. Коэффициент расхода насадка больше коэффициента расхода отверстия.

Внимание!

В задачах вычисляется число Re. Если Re > 10⁵, принимается m_отв = 0,6 ; m_нас = 0,82, j_отв = 0,97, j_нас = 0,82. В противном случае коэффициенты уточняются по графику (Приложение 9).

Пример расчета

Вода из верхней секции замкнутого бака (Рис.23) перетекает в нижнюю через отверстие диаметром d₁ = 30мм, а затем через цилиндрический насадок диаметром d₂ = 20мм вытекает в атмосферу. Температура воды 20°С.

Определить выходную скорость и расход жидкости через насадок, если показание манометра р_м = 50кПа, а уровни в водомерных стёклах H₁ = 2м и H₂ = 3м.

Чему при этом будет равно избыточное давление р_х над уровнем воды в нижней секции бака?

Решение

1. Определяем расход через отверстие по формуле (55). Поскольку в формулу входит разность давлений, можно подставлять избыточные давления.

2. Определяем расход через насадок по формуле (55).

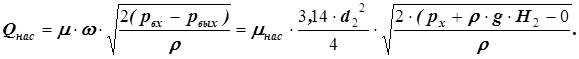
3. Приравниваем эти расходы и определяем из полученного уравнения избыточное давление р_х в общем виде.

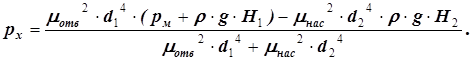
4. Подставляем исходные данные и вычисляем давление р_х.

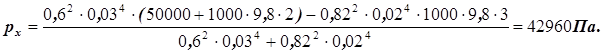
5. Вычисляем расход через насадок.

6. Вычисляем число Re.

Re_нас = 4 ×Q/(p×d×n) = 4×3,1×10^-3/3,14/0,03/1×10^-6 = 1,32×10⁵. Re_нас < Re_отв.

Так как Re > 10⁵, значения коэффициентов расхода выбраны верно.

Здесь n = 1×10^-6 м²/с – кинематический коэффициент вязкости воды (Приложение 1).

РАЗДЕЛ 5
	КОНТРОЛЬНЫЕ ЗАДАЧИ ПО ГИДРОДИНАМИКЕ

Контрольное задание включает три задачи. Выбор варианта производится по последней цифре шифра, а численных данных – по предпоследней цифре шифра зачетной книжки.

Таблица вариантов

Последняя цифра шифра	Номера задач
	10, 20, 30
	1, 11, 21
	2, 12, 22
	3, 13, 23
	4, 16, 24
	5. 17. 25
	6, 14, 26
	7, 15, 27
	8, 18, 28
	9, 19, 29

В условиях задач могут быть не указаны физические свойства жидкости, шероховатость поверхности трубопровода или некоторые другие параметры, которые выбираются из таблиц в Приложениях.

Методика решения всех задач, по существу, сводится к следующему.

· Записать уравнение или систему уравнений, выражающих законы сохранения массы и энергии.

· Записать уравнение, выражающее условие равномерного движения твердого тела, находящегося в жидкости под силовым воздействием.

· Решить полученную систему уравнений относительно неизвестной величины.

Все задачи решаются до конца в общем виде. Далее подставляются исходные данные в системе СИ и производятся вычисления с точностью до трех значащих цифр. Результат записывается в виде степени числа 10.

Например, вычисляется расход, и на калькуляторе получено число: 0,00678954. Результат нужно записать в виде: Q = 6,79×10 ^–3 м³/с.

ВНИМАНИЕ!

Перед выполнением контрольного задания изучите методику решения задач гидродинамики на базовых примерах.

Задача 1

Насос подает жидкость из подземной ёмкости с избыточным давлением газа на поверхности жидкости. На всасывающей линии (длина l, диаметр d, трубы сварные, бывшие в эксплуатации) имеются местные сопротивления: приёмная коробка с клапаном и сеткой, колено и кран с коэффициентом сопротивления x_кр. Показание вакуумметра на входе в насос равно р_v, расход жидкости Q, температура t° C.

Определить рабочую высоту всасывания насоса h_вс и предельную высоту из условия отсутствия кавитации на входе в насос. Объяснить также, почему при кавитации насос не всасывает жидкость и рабочее колесо насоса выходит из строя.

Рисунок к задачам 1, 2, 3, 4, 5

Указания

1. Определите h_вс из уравнения Бернулли для сечений 1-1 и 2-2.

2. Отрицательное избыточное давление в таблице данных – это вакуумметрическое давление.

3. При определении максимальной высоты всасывания примите давление в сечении 2-2 равным давлению насыщенного пара р_н.п. (Приложение 8).

4. При ответе на вопрос по кавитации используйте материал раздела 4.6.3. и найдите аналогию между работой сифона и насоса.

Таблица исходных данных

Вариант	l, м	d, м	pv, кПа	xкр.	ри, кПа	Q, л/с	t, °C	Жидкость
		0,1						вода
		0,05			-20			бензин
		0,06						вода
		0,08		1,5				масло инд. 20
		0,05			-40			керосин
		0,1						бензин
		0,15			-25			вода
		0,2						масло инд. 50
		0,12		2,6				диз. топливо
		0,04		3,5				масло турбинное

Задача 2

Решите задачу 1 при условии, что высота подъёма жидкости h_вс задана, а расход Q нужно определить.

Указания

Определите расход Q графическим способом (раздел 4.6.2.).

Вар-нт
hвс, м			3,5	2,8		4,6	3,6	5,3	4,1	2,5

Задача 3

Решите задачу 1 при условии, что высота подъёма жидкости h_вс задана, а диаметр трубы d нужно определить.

Указания

Определите диаметр трубы d графическим способом (раздел 4.6.2.).

Вар-нт
hвс, м			3,5	2,8		4,6	3,6	5,3	4,1	2,5

Задача 4

Решите задачу 1 при условии, что высота подъёма жидкости h_вс задана, а нужно определить максимальный расход в трубопроводе из условия отсутствия кавитации.

Указания

При определении максимального расхода примите давление в сечении 2-2 равным давлению насыщенного пара р_н.п. (Приложение 8). Далее определите из уравнения Бернулли расход графическим способом ((раздел 4.6.2.).

Вар-нт
hвс, м	3,2	5,1	3,2	4,2	4,6	3,9	4,7	5,1	3,7	4,8

Задача 5

Решите задачу 1 при условии, что высота подъёма жидкости h_вс задана, а нужно определить минимальный диаметр трубопровода из условия отсутствия кавитации.

Указания

При определении минимального диаметра трубопровода примите давление в сечении 2-2 равным давлению насыщенного пара р_н.п. (Приложение 8). Далее определите из уравнения Бернулли диаметр графическим способом (раздел 4.6.3.).

Вар-нт
hвс, м	3,2	5,1	3,2	4,2	4,6	3,9	4,7	5,1	3,7	4,8

Задача 6

Для поддержания пластового давления при добыче нефти в нагнетательную скважину глубиной H по насосно-компрессорным трубам (диаметр d, длина l, шероховатость D_э) закачивается Q м³ воды в сутки. Забойное избыточное давление равно р_заб. Температура воды t° C.

Определить показание устьевого манометра р_м и полезную мощность N_п, затрачиваемую при закачке.

Рисунок к задачам 6, 7, 8

Указания

1. Примените уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0.

2. При расчете потерь учтите только потери по длине. Местными потерями пренебречь.

3. Полезная мощность определяется по формуле: N_п = р_м × Q

4. Принять длину трубопровода равной H.

Таблица исходных данных

Вариант	H, м	d, мм	Pзаб, МПа	Dэ, мм .	Q, м^3/сутки	t°C
				0,5
				0,4
				0,3
				0,5
				0,8
				0,4
				0,3
				0,7
				1,0

Задача 7

При условии задачи 6 и известном давлении на устье определить расход воды.

Указание

Задачу решить методом итераций, предполагая турбулентный режим движения (раздел 4.6.2.).

Вар-нт
рм, МПа	6,2	5,9

Задача 8

При условии задачи 6 и известном давлении на устье определить диаметр трубопровода.

Указание

Задачу решить графическим способом ((раздел 4.6.3).

Вар-нт
рм, МПа	6,2	5,9

Задача 9

По трубопроводу (длина l, диаметр d, трубы стальные, сварные, умеренно заржавленные, åx = åx₀) вода при t° C подается к пожарному брандспойту[12] с расходом Q. Превышение обреза сопла над осью трубопровода равно h.

Определить необходимый диаметр сопла d_c и избыточное давление в начальном сечении трубопровода р_и, исходя из условия, что струя воды должна достигать высоты H. Сопротивлением воздуха пренебречь.

Рисунок к задачам 9, 10 и 11

Указания

1. Примените уравнение Бернулли для сечений 2-2 и 3-3 и определите из него скорость J_c в сечении 2-2. (J₃ =0, р₂ = р₃ = р_ат).

p×d_c²/4 = Q/J_c. – отсюда определите диаметр d_c выходного сечения сопла.

2. Показание манометра в начале трубопровода определяется из уравнения Бернулли, записанного для сечений 1-1 и 2-2.

3. Физические свойства воды определите из Приложения 1.

Таблица исходных данных

Вариант	h, м	d, мм	åx0	l, м.	Q, дм^3/с	H, м	t°C
	2,5
	1,8
	2,6
	2,2
	2,6
	2,5
	3,2

Задача 10

1. При условии задачи 9 и известном давлении на входе в трубопровод определить расход воды.

2. Определить диаметр выходного сечения сопла.

Указания

1. Примените уравнение Бернулли для сечений 2-2 и 3-3 и определите из него скорость J_c в сечении 2-2. (J₃ =0, р₂ = р₃ = р_ат).

2. Расход определите графическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 (раздел 4.6.2.).

Вар-нт
рм, кПа

Задача 11

1. При условии задачи 9 и извест-ном избыточном давлении на входе р_м определить диаметр трубопровода.

2. Определить диаметр выходного сечения сопла.

Указания

1. Примените уравнение Бернулли для сечений 2-2 и 3-3 и определите из него скорость J_c в сечении 2-2. (J₃ =0, р₂ = р₃ = р_ат).

2. Диаметр определите графическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 (раздел 4.6.2.).

Вар-нт
рм, кПа

Задача 12

Поршень диаметром D, двигаясь равномерно, всасывает жидкость из открытого бака с атмосферным давлением р_ат на поверхности жидкости. Высота всасывания равна z₀. Всасывающая труба - длина l, диаметр d, стальная, новая, сварная. Гидравлические сопротивления показаны на рисунке. Температура жидкости t° C. Атмосферное давление равно 100 кПа.

Определить максимально возможную скорость J_п поршня и силу Р, приложенную к нему, по условию кавитации в цилиндре.

Рисунок к задачам 12, 13, 14 и 15

Указания

1. Примите давление в сечении 2-2 равным давлению насыщен-ного пара (Приложение 8).

2.Определите расход из уравне-ния Бернулли (раздел 4.6.2) и далее скорость в сечении 2-2. J₂ = J_п.

3. Определите силу Р из условия равномерного движения поршня (силы показаны на рисунке).

Таблица исходных данных

Вариант	z0, м	D, мм	d, мм	l, м.	t°C	Жидкость
						вода
	2,5					бензин
						керосин
						вода
	1,8					бензин
	2,6					керосин
	2,2					вода
	2,6					бензин
	2,5					керосин
	3,2					вода

Задача 13

При условии задачи 12 и известном расходе жидкости определите минимальный диаметр трубопровода по условию кавитации.

Указания

Диаметр определите графическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 (раздел 4.6.3.). Давление в сечении 2-2 равно давлению насыщенного пара жидкости.

Вар-нт
Q, л/с	1,1	1,2	1,5		1,8	2,2	2,4	1,0	1,7	2,8

Задача 14

При условии задачи 12 и известном расходе жидкости определите высоту z₀ по условию кавитации.

Указания

Высоту z₀ определите аналитическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 (раздел 4.6.1). Давление в сечении 2-2 равно давлению насыщенного пара жидкости.

Вар-нт
Q, л/с	1,1	1,2	1,5		1,8	2,2	2,4	1,0	1,7	2,8

Задача 15

При условии задачи 12 и известной силе Р определите высоту z₀. Проверьте, имеет ли место явление кавитации в сечении 2-2.

Указания

1. Высоту z₀ определите аналитическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 ((раздел 4.6.1).

2. Сравните давление в сечении 2-2 с давлением насыщенного пара жидкости.

Вар-нт
Р, н

Задача 16

Поршень диаметром D, двигаясь равномерно со скоростью J_п, подает жидкость в закрытый бак с избыточным давлением р_м на поверхности жидкости. Разность уровней жидкости в цилиндре и баке равна z₀.

Нагнетательная труба - длина l, диаметр d, стальная, новая, сварная. Гидравлические сопротивления показаны на рисунке. Температура жидкости t° C.

Определить силу Р, приложенную к поршню.

Рисунок к задачам 16, 17, 18 и 19

Указания

1. Определите давление в сечении 1-1 из уравнения Бернулли (см. Пример 1).

2. Определите силу Р из условия равномерного движения поршня (силы показаны на рисунке).

Таблица исходных данных

Вариант	рм, МПа	z0, м	D, мм	d, мм	l, м.	Jп, см/с	t°C	Жидкость
	0,1							вода
	0,2	2,5						бензин
	0,3							керосин
	0,25							вода
	0,35	1,8						бензин
	0,15	2,6						керосин
	0,12	2,2						вода
	0,08	2,6						бензин
	0,27	2,5						керосин
	0,23	3,2						вода

Задача 17

При условии задачи 16 и известной силе Р определите высоту z₀.

Указания

1. Давление в сечении 1-1 определяется из условия равномерного движения поршня.

2. Высоту z₀ определите аналитическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 (раздел 4.6.1.).

Вар-нт
Р, н

Задача 18

При условии задачи 16 и известной силе Р определите расход жидкости.

Указания

1. Давление в сечении 1-1 определяется из условия равномерного движения поршня.

3. Расход определите графическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 (раздел 4.6.2.).

Вар-нт
Р, н

Задача 19

При условии задачи 16 и известной силе Р определите диаметр трубопровода.

Указания

1. Давление в сечении 1-1 определяется из условия равномерного движения поршня.

2. Диаметр определите графическим способом из уравнения Бернулли, записанного для сечений 1-1 и 2-2 (раздел 4.6.3).

Вар-нт
Р, н

Задача 20

Гидравлический демпфер (гаситель колебаний) представляет цилиндр, в котором под действием внешней силы R перемещается поршень. Он прогоняет масло плотностью r из одной полости цилиндра в другую через обводную трубку и регулируемый дроссель[13]. Диаметр поршня D₁, штока D₂, обводной трубки d. Коэффициент сопротивления дросселя x_др, скорость поршня J.

1. Определить неизвестную величину.

2. Получить уравнение статической характеристики демпфера, представляющей зависимость скорости равномерного движения поршня J от приложенной к нему нагрузки R. Построить график этой зависимости.

Диапазон изменения силы R – от нуля до значения в данной задаче.

Примечание: в трубе учитывать только местные гидравлические сопротивления. Утечками и трением в цилиндре пренебречь.

Рисунок к задаче 20, 21

Указания

1. Запишите уравнение Бернулли для сечений 1-1 и 2-2 и условие равномерного движения поршня (силы показаны на чертеже).

2. Определите из системы уравнений неизвестную величину и Q = f(R).

J_п =Q/w.

3. В уравнении Бернулли р₁ – р₂ = (Р₁ – Р₂)/w = R/w, где w -площадь действия давлений жидкости (кольцо).

Таблица исходных данных

Вариант	r, кг/м^3	d,мм	D1, мм	D2, мм	xдр.	Jп, см/с	R, кн
							?
						?
		?
					?
							?
							?
		6,5				?
		5,6				?
		7,2			?
		?

Задача 21

Гидравлический демпфер (Рис.20) представляет цилиндр, в котором под действием внешней силы R перемещается поршень. Он прогоняет масло плотностью r из одной полости цилиндра в другую через обводную трубку и регулируемый дроссель. Диаметр поршня D₁, штока D₂, обводной трубки d, длина трубки l. Коэффициент сопротивления дросселя x_др, скорость поршня J.

1. Определить силу на штоке.

2. Получить уравнение статической характеристики демпфера, представляющей зависимость скорости равномерного движения поршня J от приложенной к нему нагрузки R. Построить график этой зависимости. Диапазон изменения силы R – от нуля до значения в данной задаче.

Примечание: в трубе учитывать местные гидравлические сопротивления и потери на трение в обводной трубке. Утечками и трением в цилиндре пренебречь.

Указания

1. В уравнение Бернулли введите потери на трение по длине: ; здесь J - скорость движения масла в трубопроводе.

2. В уравнении Бернулли

р₁ – р₂ = (Р₁ – Р₂)/w = R/w, где w -площадь действия давлений жидкости.

3. Для всех вариантов кинематический коэффициент вязкости масла n =1×10^-4м²/с.

Таблица исходных данных

Вариант	r, кг/м^3	d,мм	D1, мм	D2, мм	xдр.	Jп, см/с	l, м
							2,5
							3,8
							3,5
		6,5					4,5
		5,6
		7,2					4,2
		8,2					2,8

Задача 22

Через отверстие диаметром d в поршне гидравлического демпфера масло плотностью r переливается из нижней полости в верхнюю полость гидроцилиндра под действием внешней нагрузки R. Диаметр гидроцилиндра D, высота поршня l, жесткость пружины с, её поджатие х.

Определить неизвестную величину.

Рисунок к задачам 22 и 23

Указания

1. Запишите систему уравнений:

- расход через отверстие (раздел 4.8).

р_вх – р_вых= Р_ж/w; Р_ж + F_пр - R =0 - условие равновесия поршня,

где w -площадь поршня, Р_ж – сила избыточного давления жидкости, F_пр = с×x –сила поджатия пружины.

2. При определении коэффициента расхода m найдите отношение l/d и сделайте выводы.

Таблица исходных данных

Вариант	r, кг/м^3	d,мм	D, мм	l, мм	с, н/мм	Q, л/с	х, мм	R, кн
						1,5		?
						?
		?				2,5
						?
								?
						1,6		?
		6,5				?
		5,6				?
		7,2				1,8		?
		?				2,6

Задача 23

Решите задачу 22 при условии, что пружина отсутствует.

Дата добавления: 2015-05-23