Модель надійності системи з поелементним резервуванням

Модель складається з основної системи, (m-1) резервних підсистем кожна з яких містить n елементів. Ймовірність безвідмовної роботи основної системи і ймовірність появи в ній відмов можна виразити формулами (5) і (6). Ймовірність безвідмовної роботи j-ї резервної системи 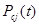із існуючих n їх груп, які містять (m-1) резервних елементів буде дорівнювати:

а ймовірність появи в ній відмови

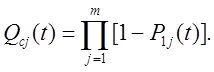
Ймовірність безвідмовної роботи системи з поелементним резервуванням 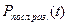буде дорівнювати:

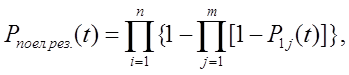(9)

а ймовірність появи в ній відмови

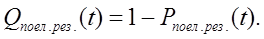
Якщо усі елементи, які входять в основну та резервну системи, мають рівноімовірну інтенсивність відмов, то вираз (9) приймає вигляд:

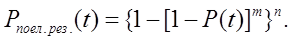
Змішане резервування. Оцінка надійності системи по моделі представленій нижче

Модель надійності системи при змішаному резервуванні

Якщо позначити надійність виділених груп (І-ІІІ) відповідно 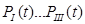, то вони будуть дорівнювати:

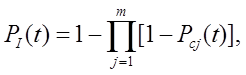
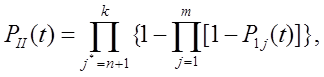
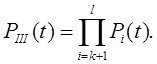
Ймоврність безвідмовної роботи системи зі змішаним резервуванням запишеться у вигляді

При цьому кількість резервних систем в группах в загальному випадку може і не співпасти. В розлянутому прикладі вони були рівними (m-1) і співпадали.

Математичний аналіз отриманих співвідношень загального і поелементного резервування показує, що поелементне резервування в n 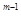разів ефективніше загального резервування.

Мажоритарне резервування є однією з різновидів структурної надлишковості. Застосовується воно для резервування цифрових схем (систем). Тут сигнал у двійковому коді (0 або 1) подається на непарну кількість ідентичних елементів. З виходів цих елементів сигнали поступають на вхід так званого вирішуючого елемента, призначенням якого є виділення з групи сигналів (серед яких можуть бути і помилкові) безпомилкового сигналу. Вирішуючий елемент видає сигнал (0 або 1) на своєму виході тільки в тому випадку, якщо на його вхід поступили аналогічні сигнали від більшості ідентичних елементів, тобто його вихідний сигнал завжди приймає значення, яке дорівнює значенню більшості вхідних сигналів.

В загальному випадку вирішуючий елемент реалізує функцію вирішення, тобто правило відображення його вхідних станів на множину вихідних. Найпростіший і найбільш розповсюджений вид цієї функції – закон більшості або мажоритарний закон. Вирішуючий елемент який реалізує мажоритарний закон називається мажоритарним елементом. Найбільше розповсюдження отримали мажоритарні елементи, які реалізують операцію „2 з З-ох”. Виконують їх як правило з логічних елементів „І” та „АБО”.

Структурна схема найпростішого мажоритарного елемента.

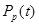Визначимо ймовірність його безвідмовної роботи. Введемо для цього наступні позначення: і – відповідно ймовірності безвідмовної роботи ідентичних і вирішуючого елементів. Скористаємося таблицею, яка відображає усі можливі стани елементів на рисунку.

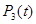
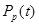
Стан відмови і працездатності в ній відповідно позначені символами 0 і 1. Будемо вважати, що вирішуючий елемент володіє ідеальною надійністю, тобто 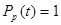, а в силу ідентичності елементів. Тоді ймовірність безвідмовної роботи мажоритарного елемента 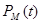може бути представлена у вигляді:

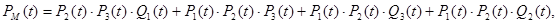(10)

де 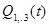– стан відмов одного – трьох ідентичних елементів. Позначемо і підставимо в (10), враховуючи, що .В результаті отримаємо:

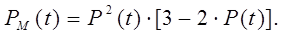
Якщо вирішуючий елемент не ідеальний, тобто 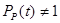, то вираз останній прийме вигляд:

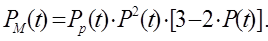
Для системи, яка складається з N послідовно увімкнених мажоритарних елементів розглянутого виду, ймовірність безвідмовної роботи 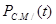має вигляд:

Якщо логічні схеми надійності не ідентичні, то мажоритарний закон не застосовується.

Дата добавления: 2015-05-23