Основные положения. Уравнение Бернулли, выражающее закон сохранения энергии для установившегося потока в поле сил тяжести

ИССЛЕДОВАНИЕ УРАВНЕНИЯ БЕРНУЛЛИ

Работа № 2

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ

Уравнение Бернулли, выражающее закон сохранения энергии для установившегося потока в поле сил тяжести, является основным уравнением гидравлики. Расчеты трубопроводов, истечения из отверстий и насадков, всасывающих и нагнетательных линий насосов основаны на применении этого уравнения.

Для потока реальной жидкости уравнение Бернулли записывается в следующей виде:

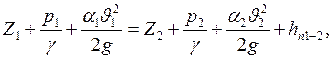(1)

где: Z₁ и Z₂ - удельная потенциальная энергия положения потока в рассматриваемых сечениях I-I и II-II на трубопроводе переменного сечения (относительно плоскости сравнения 0-0) (рис. 3.);

- удельная потенциальная энергия давления потока в тех же сечениях;

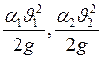- удельная кинематическая энергия потока;

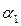и 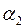- коэффициенты, учитывающие неравномерное распределение скоростей по живому сечению потока I-I и II-II;

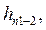- потеря энергии (напора) на преодоление гидравлических сопротивлений при движении потока от сечения I-I до сечения II-II.

Таким образом, уравнение Бернулли является энергетической характеристикой движения реальной жидкости.

Трехчлен 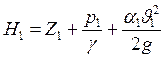называется гидродинамическим напором потока в сечении I-I и представляет собой удельную (отнесенную к единице веса) механическую энергию, проносимую потоком через это сечение.

Удельная потенциальная энергия потока в сечении I-I отнесенная к плоскости сравнения 0-0 называется пьезометрическим напором.

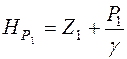. (2)

Рис. 3. Графическая иллюстрация уравнения Бернулли.

Аналогичные определения напоров можно дать для любых сечений потока.

Линия 1-1 (рис. 3), соединяющая отметки пьезометрических напоров в сечениях, называется пьезометрической линией.

Линия 2-2, соединяющая отметки гидродинамических напоров в сечениях, называется напорной линией или линией энергии.

Линия энергии по длине потока всегда опускается, т.к. энергия непрерывно расходуется на преодоление гидравлических сопротивлений.

Потеря энергии на преодоление гидравлических сопротивлений, определяется из уравнения Бернулли (1):

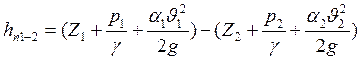
или

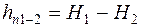. (3)

То есть потеря энергии равна разности гидравлических напоров в сечениях.

Потеря энергии, отнесенная к единице длины потока называется гидравлическим уклоном I:

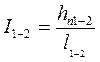(4)

где: 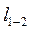- расстояние между сечениями I-I и II- II.

Энергетическую и геометрическую сущность уравнения Бернулли можно наглядно продемонстрировать на лабораторной установке.

Дата добавления: 2015-05-23