
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 4. Основные уравнения механики жидкости и газа
|
|
|
|
4.1. Модель явления – это:
а) усложненное представление явления; б) упрощенное представление явления; в) представление явления во всем объеме его свойств.
Ответ: б).
4.2. Уравнение неразрывности представляет собой математическую форму записи закона сохранения:
а) энергии; б) количества движения; в) массы; г) энтропии.
Ответ: в).
4.3. Формулировка уравнения неразрывности в интегральной форме:
а) масса жидкости в контрольном объеме неизменна; б) скорость изменения массы жидкости в контрольном объеме обусловлена разностью массовых расходов жидкости, вытекающего из объема и втекающего в него; в) масса жидкости жидкого объема изменяется с течением времени; г) скорость изменения массы жидкости в контрольном объеме равна нулю.
Ответ: б).
4.4. Скорость изменения массы жидкости в контрольном объеме равна:
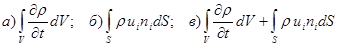 .
.
Ответ: в).
4.5. Локальная скорость изменения массы жидкости в контрольном объеме:
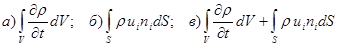 .
.
Ответ: а).
4.6. Конвективная скорость изменения массы жидкости в контрольном объеме:
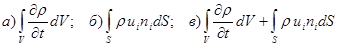 .
.
Ответ: б).
4.7. Скорость изменения любой физической величины g, отнесенной к единице объема, в объеме V, через который протекает жидкость, равна:
а) нестационарному объемному члену 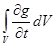 ; б) конвективному члену
; б) конвективному члену  ;
;
в) сумме локальной и конвективной составляющих 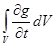 +
+  .
.
Ответ: в).
4.8. Для получения уравнения неразрывности в дифференциальной форме из интегральной формы необходимо использовать:
а) теорему Стокса; б) теорему Коши-Гельмгольца; в) теорему Остроградского-Гаусса.
Ответ: в).
4.9. Теорема, используемая для получения дифференциальной формы уравне-ния из интегральной, необходима:
а) для перевода поверхностного интеграла в объемный; б) для перевода объемного интеграла в поверхностный; в) для определения полной скорости движения жидкой частицы; г) для определения выражения для вязких напряжений.
Ответ: а).
4.10. В общем случае нестационарного пространственного движения жидкости дифференциальное уравнение неразрывности в дивергентной форме имеет вид:
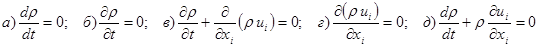 .
.
Ответ: в).
4.11. В общем случае нестационарного пространственного движения жидкости дифференциальное уравнение неразрывности в недивергентной форме имеет вид:
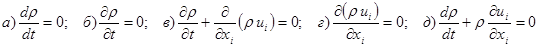 .
.
Ответ: д).
4.12. В общем случае стационарного пространственного движения жидкости дифференциальное уравнение неразрывности имеет вид:
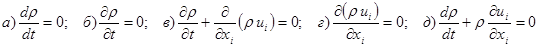 .
.
Ответ: г).
4.13. В общем случае стационарного пространственного движения жидкости интегральное уравнение неразрывности имеет вид:
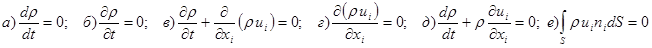 .
.
Ответ: е).
4.14. Объем, переносимый жидкостью в единицу времени через элементарную площадку dS и называемый объемным расходом, вычисляется по формуле  и будет положительным тогда, когда:
и будет положительным тогда, когда:
а) жидкость вносится через участок поверхности; б) жидкость выносится через участок поверхности; в) жидкость движется вдоль участка поверхности.
Ответ: б).
4.15. Объем, переносимый жидкостью в единицу времени через элементарную площадку dS и называемый объемным расходом, вычисляется по формуле  и будет отрицательным тогда, когда:
и будет отрицательным тогда, когда:
а) жидкость вносится через участок поверхности; б) жидкость выносится через участок поверхности; в) жидкость движется вдоль участка поверхности.
Ответ: а).
4.16. Объем, переносимый жидкостью в единицу времени через элементарную площадку dS и называемый объемным расходом, вычисляется по формуле  и будет равен нулю тогда, когда:
и будет равен нулю тогда, когда:
а) жидкость вносится через участок поверхности; б) жидкость выносится через участок поверхности; в) жидкость движется вдоль участка поверхности.
Ответ: в).
4.17. Если скалярное произведение в формуле для объемного расхода через элементарную площадку  положительно, то:
положительно, то:
а) жидкость втекает в объем; б) жидкость вытекает из объема; в) жидкость не втекает в объем; г) жидкость не вытекает из объема.
Ответ: б).
4.18. Если скалярное произведение в формуле для объемного расхода через элементарную площадку  отрицательно, то:
отрицательно, то:
а) жидкость втекает в объем; б) жидкость вытекает из объема; в) жидкость не втекает в объем; г) жидкость не вытекает из объема.
Ответ: а).
4.19. Если скалярное произведение в формуле для объемного расхода через элементарную площадку  равно нулю, то:
равно нулю, то:
а) жидкость втекает в объем; б) жидкость вытекает из объема; в) жидкость не втекает в объем; г) жидкость не вытекает из объема.
Ответ: в), г).
4.20. Массовый расход жидкости в сечении S канала вычисляется в общем случае неоднородного течения по формуле:
 .
.
Ответ: б).
4.21. Массовый расход жидкости в сечении S канала вычисляется в случае однородного (одномерного) течения по формуле:
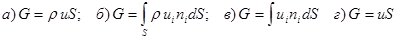 .
.
Ответ: а).
4.22. Скорость изменения количества движения жидкости в контрольном объеме V обусловлена:
а) скоростью изменения количества движения в каждой точке объема  ; б) конвективным переносом количества движения через контрольную поверхность
; б) конвективным переносом количества движения через контрольную поверхность 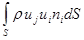 ; в) локальной и конвективной составляющими скорости изменения количества движения
; в) локальной и конвективной составляющими скорости изменения количества движения  +
+ 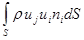 .
.
Ответ: в).
4.23. Внешние силы, действующие на жидкость в контрольном объеме, определяют:
а) количество движения жидкости в контрольном объеме; б) количество жидкости в контрольном объеме; в) скорость изменения количества движения жидкости в контрольном объеме; г) скорость изменения количества движения жидкого объема; д) количество движения жидкости в жидком объеме; е) количество жидкости в жидком объеме.
Ответ: в).
4.24. Внешними силами, определяющими скорость изменения количество движения жидкости в контрольном объеме, являются:
а) силы давления; б) силы, обусловленные вязкостью жидкости; в) массовые силы (сила тяжести, электромагнитная сила); г) силы инерции; д) силы давления и вязкие силы; е) силы давления и массовые силы; ж) все силы, кроме сил инерции.
Ответ: ж)
4.25. Если имеется интегральная форма уравнения движения, то для по-лучения его дифференциальной формы необходимо применить:
а) гипотезу Стокса; б) теорему Стокса; в) теорему Коши-Гельмгольца; г) теорему Остроградского-Гаусса.
Ответ: г).
4.26. В уравнении движения

локальной скоростью изменения количества движения жидкости в контрольном объеме является:
а) последний член в правой части; б) первый член в правой части; в) второй член в левой части; г) второй член в правой части; д) первый член в левой части уравнения.
Ответ: д).
4.27. В уравнении движения

конвективной скоростью изменения количества движения жидкости в контрольном объеме является:
а) последний член в правой части; б) первый член в правой части; в) второй член в левой части; г) второй член в правой части; д) первый член в левой части уравнения.
Ответ: в).
4.28. В уравнении движения

силой давления, определяющей скорость изменения количества движения жидкости в контрольном объеме, является:
а) последний член в правой части; б) первый член в правой части; в) второй член в левой части; г) второй член в правой части; д) первый член в левой части уравнения; е) эта сила не определяет скорость изменения количества движения и потому в уравнении отсутствует.
Ответ: б).
4.29. В уравнении движения

вязкой силой, определяющей скорость изменения количества движения жидкости в контрольном объеме, является:
а) последний член в правой части; б) первый член в правой части; в) второй член в левой части; г) второй член в правой части; д) первый член в левой части уравнения; е) эта сила не определяет скорость изменения количества движения и потому в уравнении отсутствует.
Ответ: г).
4.30. В уравнении движения

массовой силой, определяющей скорость изменения количества движения жидкости в контрольном объеме, является:
а) последний член в правой части; б) первый член в правой части; в) второй член в левой части; г) второй член в правой части; д) первый член в левой части уравнении; е) эта сила не определяет скорость изменения количества движения и потому в уравнении отсутствует.
Ответ: а).
4.31. В уравнении движения

силой инерции, определяющей скорость изменения количества движения жидкости в контрольном объеме, является:
а) последний член в правой части; б) первый член в правой части; в) второй член в левой части; г) второй член в правой части; д) первый член в левой части уравнения; е) эта сила не определяет скорость изменения количества движения и потому в уравнении отсутствует.
Ответ: е).
4.32. В дифференциальной форме уравнения движения в напряжениях
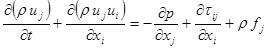 все члены отнесены к:
все члены отнесены к:
а) единице массы жидкости; б) единице объема; в) единице веса жидкости.
Ответ: б).
4.33. В дифференциальной форме уравнения движения в напряжениях
 все члены отнесены к:
все члены отнесены к:
а) единице массы жидкости; б) единице объема; в) единице веса жидкости.
Ответ: а).
4.34. Из представленных уравнений движения
1)  ; 2)
; 2)  ;
;
3) 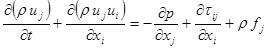
уравнением Л.Эйлера является: а) уравнение 3); б) уравнение 1); уравнение 2).
Ответ: б).
4.35. Уравнение движения Л.Эйлера относится к:
а) невесомой жидкости; б) вязкой жидкости; в) идеальной жидкости.
Ответ: в).
4.36. Выбрать формулировку закона сохранения энергии для контрольного объема:
а) изменение энергии жидкости в контрольном объеме обусловливается подводом (отводом) тепла к нему и работой, производимой напряжениями над этим объемом;
б) скорость изменения полной энергии жидкости в контрольном объеме обусловливается скоростью подвода (отвода) тепла к нему и работой, производимой напряжениями над этим объемом в единицу времени;
в) скорость изменения внутренней энергии жидкости в контрольном объеме обусловливается скоростью подвода (отвода) тепла к нему и работой, производимой напряжениями над этим объемом в единицу времени;
г) скорость изменения кинетической энергии жидкости в контрольном объеме обусловливается скоростью подвода (отвода) тепла к нему и работой, производимой напряжениями над этим объемом в единицу времени;
д) скорость изменения полной энергии жидкости в контрольном обусловливается скоростью подвода (отвода) тепла к нему и работой, производимой внутренними силами над этим объемом в единицу времени.
Ответ: б).
4.37. В механике жидкости и газа под полной энергией понимают:
а) сумму внутренней, кинетической и энергии связи молекул (атомов) жидкости; б) сумму внутренней и кинетической энергии; в) сумму внутренней энергии и энергии связи молекул; г) сумму энергии связи молекул и кинетической энергии.
Ответ: б).
4.38. Полная энергия единицы объема жидкости равна:
а) 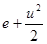 , б)
, б) 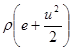 ; в)
; в) 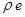 ; г)
; г) 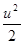 ; д) r
; д) r 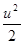 .
.
Ответ: б).
4.39. Скорость изменения полной энергии жидкости в контрольном объеме:
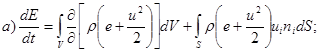


Ответ: а).
4.40. Работа, производимая в единицу времени над жидкостью в контрольном объеме поверхностными напряжениями, равна:
 б)
б) 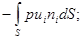

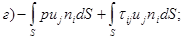
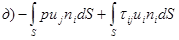 .
.
Ответ: а)
4.41. Работа массовых напряжений над жидкостью в контрольном объеме:

 в)
в) 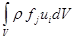 .
.
Ответ: б).
4.42. Работа, производимая силой в единицу времени, равна:
а) скалярному произведению вектора силы на вектор пути; б) векторному произведению вектора силы на вектор пути; в) скалярному произведению вектора силы на вектор скорости; г) векторному произведению вектора силы на вектор скорости.
Ответ: в).
4.43 Работа, производимая поверхностным напряжением, действующему на элемент поверхности жидкости dS, равна:
а) скалярному произведению вектора напряжения на вектор площади dS, скалярно умноженному на вектор пути; б) векторному произведению вектора напряжения на вектор площади dS, скалярно умноженному на вектор пути; в) скалярному произведению вектора напряжения на вектор площади dS, скалярно умноженному на вектор скорости; г) скалярному произведению вектора напряжения на вектор площади dS, векторно умноженному на вектор скорости.
Ответ: в).
4.44.Для подготовки записи уравнения энергии с использованием энтальпии необходимо:
а) отнять от обеих частей уравнения энергии частную производную по времени от давления; б) прибавить к обеим частям уравнения энергии частную производную по времени от давления; в) произвести преобразования уравнения энергии, не используя частной производной давления по времени.
Ответ: б).
4.45. Интегральная форма уравнения энергии относится:
а) к жидкому объему; б) к фиксированной точке пространства; в) к кон-трольному объему.
Ответ: в).
4.46. Уравнение механической энергии устанавливает связь между:
а) между скоростью изменения кинетической энергии и скоростью подвода (отвода) тепла к единице объема жидкости; б) работой перемещения единицы объема жидкости поверхностными и массовыми напряжениями и скоростью. подвода (отвода); в) скоростью изменения кинетической энергии единицы объе-ма жидкости и работой перемещения, совершаемой поверхностными и массо-выми напряжениями в единицу времени над единицей объема жидкости; г) ско-ростью изменения кинетической энергии единицы объема жидкости, работой перемещения, совершаемой поверхностными и массовыми напряжениями в единицу времени над единицей объема жидкости и скоростью подвода (отвода) тепла.
Ответ: в).
4.47. Уравнение переноса тепловой энергии показывает, что:
а) полная скорость изменения внутренней энергии единицы объема жидкости обусловлена работой деформации, совершаемой поверхностными на-пряжениями в единицу времени, и подводом тепла из окружающей среды; б) по-лная скорость изменения внутренней энергии единицы объема жидкости происходит в результате работы перемещения, совершаемой поверхностными напряжениями в единицу времени, и подвода тепла из окружающей среды; в) по-лная скорость изменения внутренней энергии единицы объема жидкости происходит в результате работы деформации, работы перемещения, совершаемой поверхностными напряжениями в единицу времени, и подвода тепла из окружающей среды.
Ответ: а).
4.48. Теорема Коши-Гельмгольца устанавливает:
а) связь между составляющими напряжений в любой точке покоящейся жидкости; б) связь между составляющими напряжений в любой точке движущейся жидкости; в) составляющие скорости в любой точке движущейся жидкости; г) составляющие скорости в любой точке покоящейся жидкости.
Ответ: в).
4.49. Уравнения Навье-Стокса являются математической записью закона:
а) сохранения массы; б) сохранения и превращения энергии; в) изменения кинетической энергии; г) переноса тепловой энергии; д) количества движения.
Ответ: д).
4.50. Отличие уравнения Навье-Стокса от уравнения движения в напряжениях заключается в:
а) использования для выражения вязких напряжений гипотезы Стокса; б) использования для выражений массовых напряжений гипотезы Стокса; в) использования для выражения давления гипотезы Стокса.
Ответ: б).
4.51. Уравнение Навье-Стокса для сжимаемой жидкости имеет вид:
а) 
 ; б)
; б)  ;
;
в) 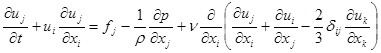
Ответ: в).
4.52. Уравнение Навье-Стокса для несжимаемой жидкости имеет вид:
а) 
 ; б)
; б)  ;
;
в) 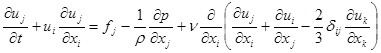
Ответ: в).
4.53. Модель течения жидкости с пограничным слоем делит вязкий поток:
а) в поперечном сечении на две области – толстый пограничный слой, в котором сосредоточено все влияние вязкости и невязкое ядро течения, в котором вязкость отсутствует; б) в поперечном сечении на две области – тонкий пограничный слой, в котором сосредоточено все влияние вязкости и невязкое ядро течения, в котором вязкость отсутствует; в) в продольном направлении на две области – начальный участок, в котором сосредоточено все влияние вязкости и основной участок течения, в котором вязкость отсу-тствует.
Ответ: б).
4.54. Из-за того, что пограничный слой тонок, давление поперек него:
а) увеличивается от давления на стенке до давления на внешней границе пограничного слоя; б) уменьшается от давления на стенке до давления на внешней границе пограничного слоя; в) постоянно поперек пограничного слоя.
Ответ: в).
4.55. В пограничном слое из-за вязкости:
а) скорость увеличивается от нуля на стенке до скорости на внешней границе пограничного слоя; б) скорость не изменяется по толщине пограничного слоя; в) скорость имеет максимум внутри пограничного слоя.
Ответ: а).
4.56. Мгновенное значение любой величины в турбулентном потока жидкости представляют:
а) значением осредненного значения величины; б) суммой осредненного значения величины и пульсационной добавки ее; в) значением пульсационного значения рассматриваемой величины.
Ответ: б).
4.57. В турбулентном течении:
а) средние значения пульсационных составляющих >0; б) средние значения пульсационных составляющих=0; в) средние значения пульсационных сос-тавляющих<0.
Ответ: б).
4.58. Уравнение Рейнольдса представляют собой:
а) уравнение неразрывности для турбулентного движения жидкости; б) уравнение движения для турбулентного движения жидкости; в) уравнение энергии для турбулентного движения жидкости.
Ответ: б).
4.59. Уравнение Рейнольдса отличаются от уравнения Навье-Стокса:
а) наличием вязких напряжением турбулентной природы; б) отсутствием вязких напряжений молекулярной природы; в) наличием пульсационной составляющей давления.
Ответ: а).
4.60. В турбулентном течении вязкость:
а) не изменяется по нормали к стенке; б) увеличивается с удалением от стенки; в) уменьшается с удалением от стенки.
Ответ: б).
4.61. Уравнение движения для неустановившегося движения вязкой жидкости имеет вид:
а)  ;
;
б)  ;
;
в)  ; г)
; г)  ;
;
г)  .
.
Ответ: а).
4.62. Уравнение движения для установившегося движения вязкой жидкости имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  .
.
Ответ: д).
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 765; Нарушение авторских прав?; Мы поможем в написании вашей работы!