Виды местных сопротивлений и определение потерь на них

Местное гидравлическое сопротивление – это короткий участок трубопровода или некоторое гидравлическое устройство на котором имеют место существенные потери энергии обусловленные изменением скорости по величине и (или) направлению и возникновением вихревых зон. При выполнении расчетов считают что местное гидравлическое сопротивление не имеет протяженности и сосредоточенности в точке.

Потери напора в местных гидравлических сопротивлениях определяется используя формулу Вейсбаха.

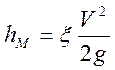(5.17)

- коэффициент местного сопротивления (б/р)

Ввиду сложности процессов на местные гидравлические сопротивления для большинства из них измеряют эксперементальным путем, при вычислениях берем из справочников.Исследованиями установлено что значение существенно зависит от числа Рейнольдса, лишь при очень низких значениях числа Рейнольдса.

В связи с тем что движение на местных гидравлических сопротивлениях не стабильно его считают турбулентным., а принимают постоянным.

При внезапном расширении происходит явление схожее с ударом упругих тел.

Для внезапного расширения принята теорема Борда-Карно:

Энергия потерянная на удар равна потерянной кинетической энергии, обусловленной уменьшением скорости движения частиц

Тогда потери напора на внезапном расширении:

Выразим потери через скорость в узком сечении:

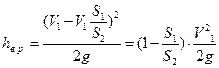(5.20)

Сравнивая 5.17 и 5.20 получим

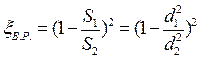(5.21)

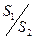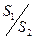
	0,1	0,5
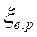
	0,81	0,25

Таким образом для внезапного расширения 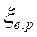=0...1.

Дата добавления: 2015-05-23