Центри мас однорідних фігур

Білет 27

1.Центр мас (центр інерції; барицентра від др.-греч. βαρύς "Важкий" і κέντρον "Центр") в механіці - це геометрична точка, що характеризує рух тіла або системи частинок як цілого. 1. Визначення. Положення центру мас (центру інерції) системи матеріальних точок в класичній механіці визначається таким чином:

де

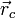- радіус-вектор центра мас,

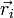- Радіус-вектор i -Й точки системи,

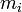- маса i -Й точки.

Для випадку неперервного розподілу мас:

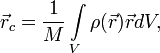
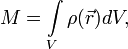
де:

- Сумарна маса системи,

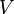- Об'єм,

- Щільність.

Центр мас, таким чином, характеризує розподіл маси по тілу або системі частинок.

• У відрізка - середина.
• У багатокутників (як суцільних плоских фігур, так і каркасів):
• У паралелограма - перетин діагоналей.
• У трикутника - точка перетину медіан (центроид).
• У правильного багатокутника - центр поворотною симетрії.

3. У механіці. Поняття центру мас широко використовується у фізиці.

Рух твердого тіла можна розглядати як суперпозицію руху центру мас і обертального руху тіла навколо його центру мас. Центр мас при цьому рухається так само, як рухалося б тіло з такою ж масою, але нескінченно малими розмірами (матеріальна точка). Останнє означає, зокрема, що для опису цього руху застосовні всі закони Ньютона. У багатьох випадках можна взагалі не враховувати розміри і форму тіла і розглядати тільки рух його центру мас.

Часто буває зручно розглядати рух замкнутої системи в системі відліку, пов'язаної з центром мас. Така система відліку називається системою центру мас (Ц-система), або системою центру інерції. У ній повний імпульс замкнутої системи завжди залишається рівним нулю, що дозволяє спростити рівняння її руху.

2.Правила Кірхгофа для розрахунку розгалужених електричних ділянок кола.
Розгалужені кола (електричні ланцюги) містять в якості основних елементів вузли та контури. Вузлами називають точки з’єднання не менш ніж трьох провідників. Приклади вузлів у колі можна побачити на рисунках 4 (вузли А та В) та 6, де вузли позначені чорними точками.

Контурами називають замкнені частини кола, які можна пройти і повернутися у вихідну точку за годинниковою стрілкою, як показано на мал.6, або в зворотному напрямі (проти стрілки). Приклади контурів можна бачити на малюнкові 3 (простий контур з однією ЕРС), на рис.4 (три контури, жодний не містить ЕРС), на рис. 6 (три контури, в кожному по дві ЕРС), на рис.5 (один контур з трьома різними ЕРС).

Щодо вузлів та контурів розгалужених схем існують два правила (два закони) Кірхгофа.

• 
  Перше правило Кірхгофа (правило вузлів):
  Алгебраїчна сума струмів у вузлі дорівнює нулю:

(3.5.21)

В сумі (3.5.21) струми, які втікають у вузол (наприклад у вузол В на рис.4 втікають три різних струми, а витікає один), і струми, що витікають, беруться з протилежними знаками. Наприклад для вузла В рис.4 з (3.5.21) маємо:

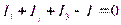(3.5.22)

• 
  Друге правило Кірхгофа (правило контурів):
  Алгебраїчна сума падінь напруги в контурі дорівнює алгебраїчній сумі ЕРС, які він містить:

3.
(3.5.23)

Струми в (3.5.23) беруться із знаком +, якщо напрям струму співпадає з напрямом обходу контуру. ЕРС в сумі правої частини (3.5.23) беруться із знаком плюс, якщо вони проходяться від негативного полюсу до позитивного, і з протилежним знаком, якщо вони проходяться у зворотному напрямі під час обходу контуру. Наприклад для контурів рис.4 та рис.5 маємо з (3.5.23):

(3.5.24)

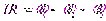(3.5.25)

Правила Кірхгофа є корисними під час розрахунків струмів та напруг в розгалужених електричних колах (ланцюгах).

Дата добавления: 2015-05-23