Хвильові рівняння електромагнітних хвиль

Для одержання хвильових рівнянь електромагнітних хвиль, розв’язком яких є рівняння (6), скористаємось рівняннями Максвелла.

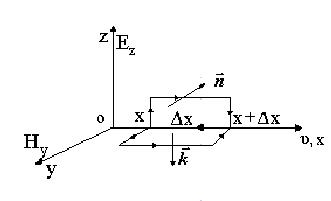
Рис. 4

Розглянемо замкнутий контур в системі координат Е_z,o,x, сторони якого відповідно дорівнюють 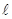і Δх. Запишемо для цього замкнутого контуру рівняння Максвелла (1)

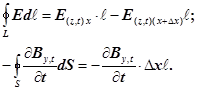
(7)

Оскільки ліві сторони рівнянь (7) відповідають рівнянню Максвелла (1), то праві сторони цих рівнянь можна прирівняти. Після незначних спрощень одержуємо

. (8)

В граничному випадку, коли рівняння (8) набуде вигляду

де – 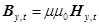, зв’язок індукції магнітного поля з напруженістю цього поля. З урахуванням цього зауваження формула (8) набуде вигляду

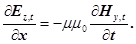(6.9)

Рівняння Максвелла (3) використаємо до замкнутого контуру в координатній площині Н_y,o,x (рис.4), вважаючи що вільні електричні заряди відсутні, а тому струм провідності jdS = 0

(10)

Оскільки ліві сторони рівнянь (10) однакові, то й праві сторони однакові. Прирівняємо праві сторони цих рівнянь, одержимо

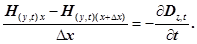
В граничному випадку, коли 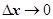, одержимо

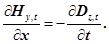(11)

Оскільки 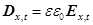, то рівняння (11) набуде вигляду

. (12)

Продиференціюємо рівняння (12) по координаті х, одержимо

(13)

Замість виразу в душках правої сторони рівняння (13) підставимо його значення з рівняння (9), одержимо

. (14)

Продиференціюємо по координаті х рівняння (9)

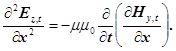(15)

Похідну в душках правої сторони рівняння (15) замінимо на відповідну похідну з рівняння (12), одержимо

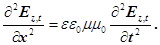(16)

З рівнянь (14) і (16) шляхом незначних перетворень одержуємо хвильові рівняння електромагнітних хвиль

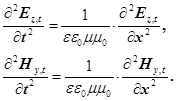(17)

Аналогічні до (17) хвильові рівняння можна одержати, якщо кожне з рівнянь (6) двічі диференціювати за часом і координатою і виключити з них функцію косинуса, тобто

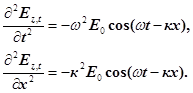
Звідки, врахувавши що 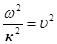, одержуємо

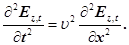(18)

Аналогічно диференціюємо друге рівняння (6) й після незначних спрощень одержуємо

(19)

Співставлення рівнянь (18) і (19) з рівняннями (17) дає можливість визначити швидкість поширення електромагнітних хвиль

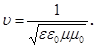(20)

Якщо врахувати, що для вакууму ε =1 і μ = 1, то швидкість поширення електромагнітних хвиль у вакуумі буде дорівнювати

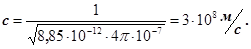(21)

Одержане значення швидкості поширення електромагнітних хвиль у вакуумі добре збігається з швидкістю поширення світла. В діелектричному середовищі (крім феромагнетиків) швидкість поширення електромагнітних хвиль менша на 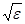, тобто

(22)

Для світлових хвиль, які можуть поширюватись в прозорих діелектричних середовищах, величину 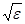називають показником заломлення і позначають через n, тому

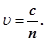(23)

Дата добавления: 2015-05-23