Ознайомитися з методикою застосування критерія Байєса. Обчислити свій варіант розрахунку. Скласти звіт

КРИТЕРІЙ БАЙЄСА

Практична робота №1

Контрольні питання

Домашнє завдання

Задача 1

У вашому розпорядженні є________ мли. грн. Ви хотіли б потроїти цю суму через _____ років. Яким є мінімально прийнятне значення процентної ставки?

Показник	Варіант студентів
Наявна сума, млн. грн.
Кількість років

Задача 2

Фірма сплачус річні дивіденди в розмірі _____ грн. на акцію, норма поточної дохідності за акціями даного типу становить ______ %. Яка має бути вартість акції?

Показник	Варіант студентів
Річний дивіденд, грн.
Норма дохідності за акціями, %

1. Сутність фінансових інвестицій та їх класифікація.

2. Що таке акція?

3.Які існують види акцій? Які основні показники обігу акцій?

3. Чим відрізняється поточна (теперішня) вартість грошових коштів від майбутньої вартості?

4. Що означає ефективна ставка процента?

5. Поясніть термін «дисконтування»?

Мета роботи:

Суть критерію — максимізація математичного сподівання функціоналу оцінювання. Назва критерію пов'язана з перетворенням формул апріорних ймовірностей у апостеріорні. Критерій Байєса часто називають критерієм середніх (сподіваних) затрат (критерієм ризику при ).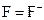

Згідно з критерієм Байєса оптимальними розв'язками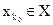

(або множиною таких оптимальних рішень) вважаються такі рішення, для котрих математичне сподівання функціоналу оцінювання досягає найбільшого можливого значення.

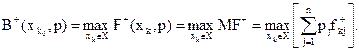(5.7)

Якщо максимум досягається _на декількох рішеннях з X, множину яких позначимо через 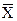, то такі рішення називають еквівалентними.

Величина

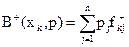
називається байєсівським значенням функціоналу оцінювання для рішення 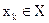. Критерій Байєса є найбільш розповсюдженим в інформаційній ситуації I₁. Цей критерій тісно пов’язаний з аксіомами теорії корисності (аксіома Неймана та Моргенштерна), де сумарна сподівана корисність визначається як математичне сподівання поросностей окремих результатів.

Якщо функціонал оцінювання задано у формі F^-, то замість оператора max математичного сподівання використовується min математичного сподівання. Якщо функціонал оцінювання задано в ризиках, то відповідну величину 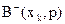називають байєсівським ризиком для розв'язку .

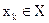У першій інформаційній ситуації I₁, при прийнятті рішень за умов ризику користуються апріорними ймовірностями. Інколи є можливим провести експеримент щодо досліджуваної системи, аналізуючи його результати, змінити апріорні ймовірності у відповідності з одержаною інформацією. Такі ймовірності називають апостеріорними.

Приклад. Підприємство випускає певну продукцію партіями фіксованого розміру. Через випадкові збої у виробничому процесі можливий випуск партій з неприпустимо високим відсотком бракованої продукції. Визначають стани економічного середовища: 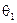—придатна партія виробів, 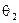—бракована партія виробів.

Нехай браковані вироби у придатній партії складають 4 %, в непридатній — 15 %. Проведені на підприємстві розрахунки показують, що ймовірність виробництва бракованої партії дорівнює 0,20 і, отже, придатна для відправки споживачам партія має ймовірність 0,80. Таким чином, .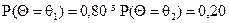

Підприємство відправляє партії товарів двом споживачам А та Б. Контрактом обумовлено, що відсоток бракованих деталей, які відправляються споживачам А та Б, не повинен перевищувати 5 та 8 % відповідно. За один відсоток перевищення встановлених меж передбачається штраф розміром 100 млн. крб. З іншого боку, виробництво партії товарів більш високої якості збільшує затрати підприємства на 80 млн. крб. за кожен відсоток.

У задачі існують два варіанти рішень (дві альтернативи): х, — відправити партію товарів споживачеві А, х₂ —відправити партію товарів споживачеві Б.

Припустимо також, що підприємець (менеджер) вирішує перевірити два вироби з усієї партії. В результаті перевірки може бути встановлено, що: 1) обидва вироби придатні; 2) один з виробів придатний; 3) обидва вироби браковані. Нехай — позначають ці три можливі події відповідно.

Підприємець повинен прийняти рішення, кому із споживачів А чи Б відправляти певну партію виробів.

Розв'язання. Функціонал оцінювання у цій ситуації доцільно подати у вигляді матриці затрат (в млн. крб.) .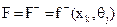

Рішення х₁ припускає, що споживач А прийме партію виробів (5 % браку без штрафу). Якщо партія має 4 % браку (8,), виробник понесе збитки (5 - 4) • 80 = 80 млн. крб. Але, якщо партія товарів буде мати 15 % браку(9₂), то штраф складе (15 - 5) • 100 = 1000 млн. крб. Аналогічно щодо рішення х₁, відправляючи споживачеві Б партію, яка містить 4 % браку (9,), виробник понесе збитки (8 - 4) • 80 = 320 млн. крб. Якщо партія містить 15 % браку (9₂), штраф складе (15 - 8) • 100 = 700 млн. крб. Отже, маємо

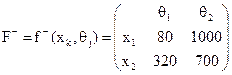
Зазначимо що, коли підприємець хоче обрати рішення, яке виключає збитки від штрафу (принцип гарантованого результату за критерієм Вальда), тобто безризикове рішення, то він повинен відправити партію виробів споживачеві Б. (Перевірте.)

Коли підприємець приймає рішення, користуючись (це суттєво) наявною інформацією щодо 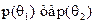то, використовуючи критерій Байєса, одержимо

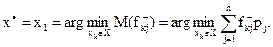
тобто партію виробів доцільно відправляти споживачеві А. (Перевірте.)

Відзначимо, що рішення підприємця повинно залежати від результатів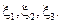

Оскільки вироби можуть обиратися як з придатної, так і з бракованої партій, то визначені умовні ймовірності 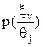. Наша мета — використати ці ймовірності разом з апріорними ймовірностями для підрахунку апостеріорних імовірностей, які позначають як 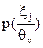. Тобто, потрібно обчислити ймовірність вибору придатної (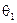) чи бракованої (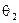) партії за результатами експерименту 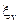. Ці ймовірності є важливим інструментом для прийняття рішень залежно від результатів контрольної перевірки.

Щоб показати, як апостеріорні ймовірності 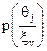знаходяться з апріорних імовірностей 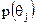та умовних імовірностей 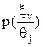розглянемо загальний випадок, коли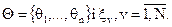

Оскільки

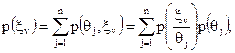(5.8)

та апостеріорні ймовірності задаються співвідношенням

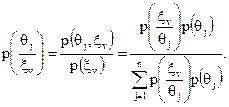(5.9)

Ці ймовірності відомі як байєсівські ймовірності.

Припустимо тепер, що у нашому прикладі браковані вироби у придатній партії складають 4 %, а в непридатній — 15% Використовуючи біномінальний закон розподілу та вибірку розміром 2, можна обчислити значення умовних ймовірностей множини подій Nn залежно від якості партії виробів:

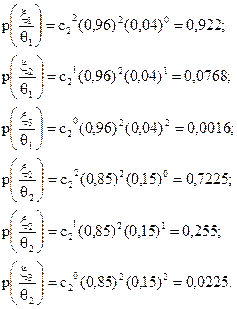
Представимо обчислені 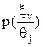ймовірності:

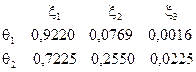
Спільні ймовірності 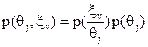можуть бути визначені з попередньої таблиці множенням першого рядка на 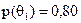і другого – на 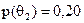отже маємо значення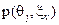

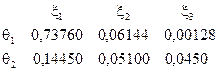
Визначимо тепер 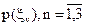за формулою (5.8).

Ці величини знаходимо підсумуванням рядків попередньої матриці:

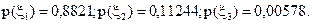
Апостеріорні ймовірності знаходимо за формулою (5.9).

Вони обчислюються діленням відповідних елементів останньої таблиці на відповідні величини . Отже, маємо значення :

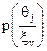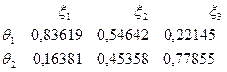
Остаточне рішення залежить від результатів контрольної перевірки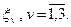

За критерієм Байєса загальна формула для підрахунку сподіваних затрат має вид:

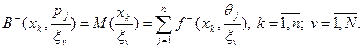(5.10)

Для нашого прикладу маємо три випадки ().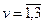

Випадок1. Подія 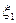(обидва вироби придатні):

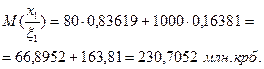
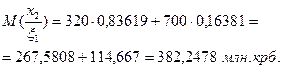
Мінімум сподіваних значень досягається при 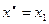. Таким чином, у цьому випадку рішення полягає у відправленні партії товарів споживачеві А, бо за критерієм Байєса рішення 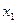гарантує менші сподівання затрати.

Випадок2. Подія 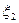(один з двох виробів є придатним):

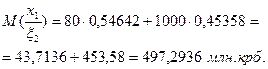
У цьому випадку рішення полягає у відправленні партії товарів споживачеві Б, бо х₂, за критерієм Байєса забезпечує менші сподівані затрати.

Випадок 3. Подія 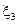(обидва вироби браковані)

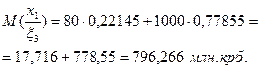
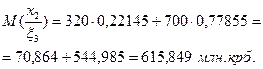
Оскільки мінімум сподіваних затрат за критерієм Байєса досягається при х = х₂, то рішення підприємця полягає у відправленні продукції споживачеві Б.

Варіант №	Р1	Р2
	0,71	0,29
	0,72	0,28
	0,73	0,27
	0,74	0,26
	0,75	0,25
	0,76	0,24
	0,77	0,23
	0,78	0,22
	0,79	0,21
	0,9	0,1
	0,81	0,19
	0,82	0,18
	0,83	0,17
	0,84	0,16
	0,85	0,15
	0,86	0,14
	0,87	0,13
	0,88	0,12
	0,89	0,11
	0,9	0,1

Дата добавления: 2015-05-23