Мета роботи. · визначити момент інерції тіла складної геометричної форми

· визначити момент інерції тіла складної геометричної форми

Теоретичні відомості. Момент інерції макроскопічного тіла можна знайти розбиттям тіла на нескінченно малі маси і розглянути їх як точкові. При цьому момент інерції тіла дорівнює сумі моментів інерції його складових

або для однорідного тіла . (1.4)

Тобто, момент інерції однорідного тіла правильної геометричної форми можна визначити розрахунково із (1.4). Моменти інерції тіл складної геометричної форми за звичай визначають експериментально.

Одним із методів експериментального визначення моменту інерції тіла є метод Гауса, заснований на використанні обертальних чи крутильних коливань.

Крутильний маятник ¾ макроскопічне тіло з моментом інерції J, закріплене нерухомо на пружному стержні (Рис.1.4). Коливання визначаються кутом відхилення тіла від положення рівноваги, вектором кутової швидкості 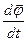та вектором кутового прискорення . Тіло здійснює малі періодичні коливання під дією моменту 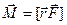зовнішньої сили 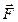, моменту 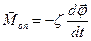сили опору та моменту 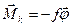пружної сили деформації кручення . Кефіцієнт f називається модулем кручення. Лінійна залежність моменту сил кручення від кута повороту виконується лише для малих коливань.

За другим законом Ньютона для обертового руху, рівняння коливань маятника можна записати так:

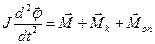. (2.4)

Вектори 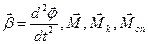лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній, векторне рівняння (2.4) можна записати в алгебраїчній формі:

,

і в канонічному вигляді:

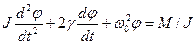, (3.4)

де 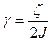¾ коефіцієнт згасання коливань, , w₀ ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника

. (4.4)

Період вільного гармонічного коливання тим більше, чим більше момент інерції тіла і чим менша пружність стержня (дроту), на якій воно закріплене.

Виміривши період Т крутильних коливань, можна визначити момент інерції тіла, яке здійснює ці коливання. Однак для цього необхідно знати модуль крутіння f.

Метод Гауса полягає в застосуванні крутильних коливань і виключенні невідомого значення модуля крутіння f з використанням пробного (еталонного) тіла з відомим моментом інерції.

Період коливань вимірюють двічі:

а) для досліджуваного тіла, для якого період коливань маятника

,

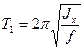б) для тіла, складеного з досліджуваного тіла з моментом інерції J_х і пробного (еталонного) тіла з моментом інерції J. якщо їх центри мас знаходяться на вісі обертання, період коливань складеного тіла визначається за формулою,

.

Звівши обидві частини виражень для періодів у квадрат і, поділивши одне на друге, одержимо пропорцію

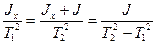
з якої випливає

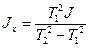. (5.4)

Момент інерції пробного (еталонного) тіла J, в якості якого, як правило, вибирають однорідне тіло провильної геометричної форми (куля, циліндричне кільце, куб, паралеліпіпед та інш.) тому, що його момент інерції можна розрахувати за формулою (1.4).

На приклад, момент інерції циліндричного кільця відносно вісі, що співпадає з геометричною віссю, дорівнює

, (6.4)

де R і r - відповідно зовнішній і внутрішній радіуси кільця, а d₁ і d₂ їхні діаметри, m ¾ маса кільця.

Момент інерції суцільного однорідного циліндра масою m і радіуса R відносно вісі, що співпадає з геометричною віссю, дорівнює

. (7.4)

Куля масою m і радіуса R має момент інерцї

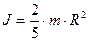. (8.4)

Геометричні розміри пробного тіла вимірюють штангенциркулем, а масу знаходять зважуванням на вагах.

Періоди коливань Т₁ і Т₂ досліджуваного й складного тіла визначають, вимірюючи час N =10¸20 коливань секундоміром (t₁ і t₂).

Дата добавления: 2015-05-23