Мета роботи. Дослідження фізичного маятника

Дослідження фізичного маятника

Контрольні питання

1. Що ми називаємо математичним маятником?

2. Коливальний рух. Гармонічний коливальний рух.

3. Вивести диференціальне рівняння незгасаючих гармонічних коливань і знайти його розв’язок.

4. Амплітуда, частота, період і фаза коливань.

5. Зміщення, швидкість, прискорення в коливальному русі.

6. енергія гармонічного коливального руху і особливості виконання закону збереження енергії.

ЛІТЕРАТУРА

1.40. Кучерук І.М., Горбачук І.Т., Луцик П.П.. Загальний курс фізики: Навчальний посібник. –Т. 1.: Механіка. Молекулярна фізика і термодинаміка. – К.: Техніка, 1999. – 536 с.

2.40. Дущенко В.П., Кучерук І.М. Загальна фізика. Фізичні основи механіки. Молекулярна фізика і термодинаміка. – К.: Вища школа, 1993. – 431 с.

3.40. Загальна фізика. Лабораторний практикум: Навч. посібник за заг.ред. І.Т. Горбачука. – К.: Вища школа, 1992. – 509 с.

4.40. Д.В. Сивухин. Общий курс физики. Т. І. Механика. – М.: Наука, 1989. – 576 с.

5.40. Трофимова Т.И. Курс физики. – М.: Высш. шк., 2000. – 478 с.

6.40. А.О.Потапов, А.І.Мотіна. Опрацювання результатів вимірювання при виконанні лабораторних робіт фізичного практикума з використанням математичної системи Mcad. (Методичні вказівки до лабораторного практикуму для студентів усіх спеціальностей). - К.: КНУТД, 2004.- 112 с.

Лабораторна робота № 41-1.

Дослідити згасаючі коливання фізичного маятника і за виміряним числом повних коливань N_t і часу релаксації t обчислити:

· сталу згасання g,

· коефіцієнт опору r,

· логарифмічний декремент згасання l,

· добротність коливальної системи Q,

оцінити коефіцієнт тертя кочення.

Теоретичні відомості:

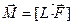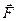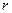Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла O_c на вектор . Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту зовнішніх сил , моменту сили тяжіння та моменту сил опору , де ¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: М_g = mgLsinj. Для малих коливань маятника маємо sinj­» j і М_g = mgLj.

Використовуючи другий закон Ньютона для обертового руху, рівняння коливань можна записати так:

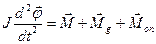, (1.41)

де J ¾ момент інерції тіла. Вектори 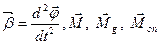лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:

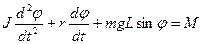. (2.41)

В канонічному вигляді рівняння (2.41) можна записати так

, (3.41)

де 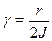¾ коефіцієнт згасання коливань, 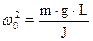, w₀ ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T₀ = 2p/w₀ і T₀ = 2p , де l_пр = 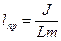¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)

Розв'язок (3.41) шукаємо підстановкою Ейлера j=e^lt.

Знайдемо перші дві похідні від j по часу

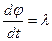e^lt, = l²e^lt. (4.41)

Підставляючи похідні (4.41) в (3.41), одержимо:

e^lt (l² + 2gl + w₀² ) = 0. (5.41)

Квадратне рівняння l² + 2gl + w₀² = 0 в (5.41) називається характеристичним. Його розв'язок

, (6.41)

дає два фундаментальні розв'язки диференціального рівняння

j₁ = exp(l₁t), j₂ = exp(l₂t), (7.41)

з яких утворюється загальний розв'язок. Загальним розв'язком однорідного рівняння (3.41) буде лінійна комбінація фундаментальних розв'язків

j = Аexp(l₁t) + Bexp(l₂t) (8.41)

з дійсними коефіцієнтами А, В.

Якісно розрізняють два випадки руху маятника:

1) При g > w₀ ¾ аперіодичний рух. При цьому l₁,l₂ < 0 ¾ дійсні числа. Функція j є спадною функцією часу (l₁,l₂<0) і описує асимптотичне, в експоненційній залежності від часу, повернення маятника в стан рівноваги. При цьому коливальний рух не здійснюється.

2) Якщо g < w₀, маятник буде здійснювати коливальний рух. При цьому

l₁ = - g­­+іw, l₂ = - g­­-іw, (9.41)

де і = 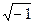¾ уявна одиниця, w = 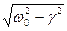¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд:

j = e^-gt(Ae^iwt + Be^-iwt) (10.41)

з комплексними коефіцієнтами А, В. Для знаходження величин А та В зауважимо, що функція j є дійсною функцією часу, і за цим вона має дорівнювати своїй комплексно спряженій функції j = j^* Þ

e^-gt(Ae^iwt+Be^-iwt) = e^-gt(A*e^-iwt +B*e^iwt). (11.41)

Прирівнюючи в (11.41) коефіцієнти при однакових експонентах, одержимо В=А *. Для зручності комплексну сталу А візьмемо в експоненціальному вигляді

А = а₀e^ia/2, де а₀ ¾ дійсна величина. Тепер

j = а₀/2·e^-gt (e^i(wt+a) +e^-i(wt+a)) (12.41)

і, користуючись формулою Ейлера e^±ix = cosx ± i×sinx, вираз в дужках запишемо у вигляді:

j = 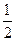а₀e^-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ

j = j₀(t)×cos(wt+a). (13.41)

В (13.41) j₀(t) = a₀e^-gt ¾ амплітуда коливань ¾ спадна функція часу, Ф = wt+a ¾ фаза коливань, Ф₀ = a ¾ початкова фаза.

Дата добавления: 2015-05-23