
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная РАБОТА
|
|
|
|
Раздел 1. Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
1.1 Диск массой m = 10 кг и радиусом R = 50 см, был раскручен до частоты n = 360 об/мин. Под действием силы трения диск остановился через время t = 20 с. Найти момент сил трения M z, считая его постоянным. (M z = 4,71 Н×м)
1.2 Определить момент инерции тела Jz, относительно оси вращения ОZ, если под действием момента силы M z = 150 H∙м за время t = 1 мин оно увеличило частоту вращения от ν 1 = 60 с-1 до ν 2 = 180 с-1. (Jz = 11,9 кг×м2)
1.3 Однородный сплошной диск массой m = 800 г и радиусом R = 20 см остановился под действием момента силы трения Mz = 10 Н·м за время t = 4 с. Определить начальную угловую скорость w 0 маховика. (w0 = 2500 рад/с)
1.4 Сплошной цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m 1 = 12 кг. На цилиндр намотан шнур, к которому привязана гиря массой m 2 = 1 кг. С каким ускорением а будет опускаться гиря? (а = 1,64 м/с2)
1.5 Маховик в виде сплошного диска массой m = 4 кг и радиусом R = 20 см начинает вращаться с угловой скоростью w = 750 рад/с под действием момента силы. Определить момент силы Mz через t = 5 с после начала вращения. (Mz = 12 Н·м)
1.6 На обод маховика диаметром D = 60 см намотан шнур, к концу которого приложена сила F. Он, вращаясь равноускоренно, за время t = 3 с изменил угловую скорость от w 0 = 0 до w = 9 рад/с. Момент инерции Jz = 0,2 кг×м2. Определить приложенную силу. (F = 2 Н)
1.7
| Z |
| d 2 |
| d 1 |
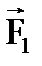
|
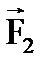
|
| A |
| B |
1.8 Колесо массой m = 2 кг и диаметром D = 1 м, представляет собой тонкий обруч со спицами, массой которых можно пренебречь, вращающийся вокруг оси OZ. Какую силу F нужно приложить к обручу, чтобы угловое ускорение колеса было равно ε = 3 рад/с2? (F = 3 H)
1.9 Маховик (в виде диска) диаметром D = 40 см и массой т 1 = 0,1 кг может вращаться вокруг горизонтальной оси, проходящей через центр масс. На обод маховика намотан шнур, к концу которого привязан груз массой m 2 = 2 кг. Определить с каким ускорением а будет опускаться груз. (а = 9,57 м/с2)
1.10 Шар массой m = 2 кг и радиусом R = 20 см начинает вращаться с угловой скоростью w = 625 рад/с под действием момента силы Mz. Определить момент силы шара Mz через t = 2 с после начала вращения. (Mz = 10 Н·м)
1.11
| А |
| F |
| a |
| O |
| Z |
1.12 По касательной к шкиву маховика в виде однородного диска диаметром D = 80 см и массой m = 40 кг приложена сила F = 1 кН. Определить угловое ускорение ε и частоту вращения n маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь. (e = 37,5 рад/с2, п = 60 об/с)
1.13 Однородный стержень длиной ℓ = 1 м и массой m = 0,5 кг вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Найти угловое ускорение ε и частоту вращения n стержня в момент времени t = 5 с под действием вращающего момента Mz = 0,05 Н·м. (e = 1,2 рад/с2, п ≈ 0,96 об/с)
1.14 Каков момент инерции Jz маховика (сплошного диска), если под действием силы натяжения F = 1 кН троса, намотанного на маховик, он за время t = 15 c изменил угловую скорость от w 0 = 0 до w = 30 рад/с? Диаметр маховика D = 50 см. (Jz = 125 кг×м2)
1.15 Маховик, имеющий форму диска массой m = 30 кг и радиусом R = 10 см, был раскручен до частоты n = 300 об/мин. Под действием силы трения диск остановился через время t = 20 с. Найти момент сил трения Mz, считая его постоянным. (Mz = 0,24 Н×м)
1.16 С какой силой F нужно тянуть за нить, намотанную на блок в виде сплошного диска радиусом R = 8 см и массой m = 200 г, чтобы сообщить ему угловое ускорение ε = 2 рад/c2? (F = 16 мH)
1.17 Диск радиусом R = 30 см и массой m = 10 кг вращается с частотой n = 5 об/c. Какой момент силы Mz следует приложить, чтобы диск остановился за время t = 10 с? (Mz = 1,41 Н×м)
1.18
| А |
| F |
| a |
| O |
| Z |
1.19 Молотильный барабан вращается с частотой f = 20 с-1. Момент инерции барабана относительно оси вращения Iz = 30 кг·м2. Определить момент силы относительно оси вращения Mz, под действием которого барабан остановится за время t = 200 с. (Mz = 18,85 Н×м)
1.20 Определить момент силы Мz, который необходимо приложить к блоку, вращающемуся с частотой n = 12 об/с, чтобы он остановился через время t = 8 с. Диаметр блока D = 20 см. Массу блока m = 6 кг считать равномерно распределенной по ободу. (Мz = 0,57 Н×м)
Раздел 2. Абсолютно упругий и неупругий удары
2.1 Две шайбы одинаковой массы движутся навстречу друг другу. После абсолютно упругого удара шайбы разлетаются в разные стороны со скоростями u 1 = 5 м/с и u 2 = 3 м/с. Определить скорости v 1 и v 2 шайб до удара.
2.2 На идеально гладкой горизонтальной плоскости лежит тело массой m 1 = 10 кг. На него налетает тело массой m 2 = 5 кг, скорость которого v2 = 5 м/c. Между телами происходит упругий центральный удар. Определить скорости u 1 и u 2 тел после удара.
2.3 Два тела массами m 1 = 2 кг и m 2 = 4 кг движутся в одном направлении со скоростями v1 = 2 м/с и v2 = 6 м/с. Найти скорости u 1 и u 2 тел после абсолютно упругого центрального удара.
2.4 Упругая шайба, движущаяся со скоростью v1 = 5 м/c, налетает на покоящуюся шайбу такой же массы. Найти скорости u 1 и u 2 шайб после центрального удара.
2.5 Тело массой m 1 = 5 кг покоится. На него налетает другое тело массой m 2 = 3 кг, движущееся со скоростью v2 = 1 м/c. Определить скорости u 1 и u 2 тел после абсолютно упругого центрального удара.
2.6 Тело массой 2,5 кг, движущееся со скоростью3 м/с, ударяется о неподвижное тело массой 5 кг. Определить скорости u 1 и u 2 тел после абсолютно упругого центрального удара.
2.7 Предмет массой m 1 = 5 кг движется со скоростью v1 = 1 м/с и сталкивается с покоящимся предметом массой m 2 = 3 кг. Определить скорости u 1 и u 2 предметов после удара. Удар считать абсолютно упругим, прямым, центральным.
2.8 Два тела массами m 1 = 2 кг и m 2 = 3 кг движутся навстречу друг другу со скоростями v1 = 3 м/с и v2 = 2 м/с. Найти скорости u 1 и u 2 тел после абсолютно упругого центрального удара.
2.9 Два тела массами m 1 = 1 кг и m 2 = 2 кг движутся в одном направлении со скоростями v1 = 6 м/с и v2 = 2 м/с. Найти скорости u 1 и u 2 тел после абсолютно упругого центрального удара.
2.10 Два тела массами m 1 = m 2 = 40 г движутся навстречу друг другу со скоростями v1 = 3 м/с и v2 = 8 м/с. Определить их скорости u 1 и u 2 после абсолютно упругого удара.
2.11 На идеально гладкой горизонтальной плоскости лежит тело массой m 1 = 2 кг. На него налетает тело массой m 2 = 4 кг, скорость которого v2 = 5 м/c. Между телами происходит упругий центральный удар. Определить скорости u 1 и u 2 тел после удара.
2.12 Два тела массами m 1 = 5 кг и m 2 = 3 кг движутся в одном направлении со скоростями v1 = 4 м/с и v2 = 3 м/с. Найти скорости u 1 и u 2 тел после абсолютно упругого центрального удара.
2.13 Вагонетка массой m 1 = 20 т, движущаяся со скоростью v1 = 36 км/ч, налетает на неподвижную вагонетку массой m 2 = 40 т. Считая удар абсолютно упругим, определить скорости u 1 и u 2 вагонеток после удара.
2.14 Шайба, движущаяся со скоростью v1 = 5 м/с, догоняет другую шайбу, движущуюся со скоростью v2 = 2 м/с. Определить скорости u 1 и u 2 шайб после абсолютно упругого центрального удара, если масса первой шайбы в два раза больше массы второй шайбы.
2.15 Тело массой m 1 = 1 кг движется со скоростью v 1 = 4 м/с и сталкивается с телом массой m 2 = 2 кг, движущимся навстречу ему со скоростью v 2 = 3 м/с. Определить скорости u 1 и u 2 тел после удара. Удар считать абсолютно упругим, прямым, центральным.
2.16 После абсолютно упругого удара две одинаковые шайбы разлетелись в разные стороны со скоростями u 1 = 5 м/с и u 2 = 10 м/с. Определить скорости v1 и v2 шайб до удара.
2.17 Две тележки массами m 1 = 40 кг и m 2 = 60 кг движутся навстречу друг другу. Найти скорости u 1 и u 2 тележек до удара, если после абсолютно упругого удара тележки движутся в разные стороны со скоростями v1 = 2 м/с и v2 = 3 м/с.
2.18 Тело массы m 1 = 1 кг, движущееся со скоростью v1 = 3 м/с, сталкивается с покоящимся телом массы m 2 = 2 кг. Найти скорости u 1 и u 2 тел после столкновения. Столкновение считать абсолютно упругим, центральным.
2.19 Два тела с массами m 1 = 2 кг и m 2 = 4 кг движутся навстречу друг другу с одинаковыми скоростями v1 = v2 = 3 м/с. Определить скорости u 1 и u 2 тел после абсолютно упругого центрального удара.
2.20 Два тела движутся навстречу друг другу со скоростями v 1 = 2 м/с и v 2 = 4 м/с. Масса второго тела в три раза больше, чем первого. Найти скорости u 1 и u 2 тел после центрального абсолютно упругого удара.
Раздел 3. Мощность тепловых потерь двухслойной конструкции
Рассчитать тепловые потери двухслойной конструкции площадью S с толщиной наружного и внутреннего слоев Δ X 1 и Δ X 2, имеющих коэффициенты теплопроводности l 1 и l 2 соответственно. Определить температуру на границе слоев. Температура снаружи конструкции Т 1 = -200С, на границе между слоями Т 2, внутри конструкции Т 3 = +200С.
| Задача | S, м2 | Δ X 1,м | Δ X 2,м | l 1, Вт/м∙К | l 2, Вт/м∙К |
| 3.1 | 0,37 | 0,06 | Кирпич пустотелый – 0,44 | ПВХ – 0,19 | |
| 3.2 | 0,12 | 0,04 | Кирпич силикатный – 0,81 | Штукатурка цементная – 0,9 | |
| 3.3 | 0,37 | 0,03 | Кирпич шлаковый – 0,58 | Битум – 0,47 | |
| 3.4 | 0,51 | 0,10 | Кирпич силикатный – 0,81 | Гипс строительный – 0,35 | |
| 3.5 | 0,34 | 0,05 | Бетон сплошной – 1,75 | Древесина — доски – 0,15 | |
| 3.6 | 0,45 | 0,05 | Бетон на каменном щебне – 1,3 | ПВХ – 0,19 | |
| 3.7 | 0,42 | 0,07 | Бетон на песке – 0,7 | Пробковые листы легкие – 0,035 | |
| 3.8 | 0,23 | 0,02 | Пенобетон – 0,3 | Гудрон - 0,3 | |
| 3.9 | 0,48 | 0,01 | Керамзитобетон – 0,2 | Рубероид – 0,17 | |
| 3.10 | 0,27 | 0,09 | Древесина твердых пород – 0,2 | Стекловолокно – 0,036 | |
| 3.11 | 0,37 | 0,04 | Кирпич пустотелый – 0,44 | Штукатурка цементная – 0,9 | |
| 3.12 | 0,51 | 0,05 | Кирпич силикатный – 0,81 | Древесина — доски – 0,15 | |
| 3.13 | 0,25 | 0,01 | Кирпич шлаковый – 0,58 | Гудрон - 0,3 | |
| 3.14 | 0,63 | 0,07 | Кирпич силикатный – 0,81 | ПВХ – 0,19 | |
| 3.15 | 0,42 | 0,06 | Бетон сплошной – 1,75 | Стекловолокно – 0,036 | |
| 3.16 | 0,38 | 0,004 | Бетон на каменном щебне – 1,3 | Рубероид – 0,17 | |
| 3.17 | 0,28 | 0,03 | Бетон на песке – 0,7 | Пробковые листы легкие – 0,035 | |
| 3.18 | 0,22 | 0,02 | Пенобетон – 0,3 | Штукатурка цементная – 0,9 | |
| 3.19 | 0,43 | 0,01 | Керамзитобетон – 0,2 | Битум – 0,47 | |
| 3.20 | 0,19 | 0,04 | Древесина твердых пород – 0,2 | Штукатурка сухая – 0,21 |
Раздел 4. Мощность тепловых потерь трехслойной конструкции
Рассчитать тепловые потери трехслойной конструкции площадью S с толщиной наружного, среднего и внутреннего слоев Δ X 1, Δ X 2, Δ X 3, имеющих коэффициенты теплопроводности l 1, l 2, l 3 соответственно. Определить температуру на границах слоев. Температура снаружи конструкции Т 1 = -200С, на границе между слоями Т 2 и Т 3, внутри конструкции Т 4 = +200С. Тепловым сопротивлением на границах между слоями пренебречь.
| Задача | S, м2 | Δ X 1,м | Δ X 2,м | Δ X 3,м | l 1, Вт/м∙К | l 2, Вт/м∙К | l 3, Вт/м∙К |
| 4.1 | 0,51 | 0,08 | 0,04 | Кирпич пустотелый – 0,44 | Пенопласт резопен ФРП – 0,045 | Штукатурка сухая – 0,21 | |
| 4.2 | 0,25 | 0,07 | 0,06 | Кирпич силикатный – 0,81 | Каучук вспененный – 0,03 | Штукатурка цементная – 0,9 | |
| 4.3 | 0,37 | 0,06 | 0,05 | Кирпич шлаковый – 0,58 | Вата минеральная легкая – 0,045 | Битум – 0,47 | |
| 4.4 | 0,51 | 0,04 | 0,05 | Кирпич силикатный – 0,81 | Картон строительный многослойный – 0,13 | Гипс строительный – 0,35 | |
| 4.5 | 0,34 | 0,09 | 0,07 | Бетон сплошной – 1,75 | Опилки - засыпка – 0,095 | Древесина - доски – 0,15 | |
| 4.6 | 0,55 | 0,05 | 0,03 | Бетон на каменном щебне – 1,3 | Пенопласт ПС-1 – 0,037 | ПВХ – 0,19 | |
| 4.7 | 0,22 | 0,04 | 0,04 | Бетон на песке – 0,7 | Пенопласт резопен ФРП – 0,045 | Пробковые листы легкие – 0,035 | |
| 4.8 | 0,43 | 0,08 | 0,01 | Пенобетон – 0,3 | Стружки - набивка – 0,12 | Гудрон - 0,3 | |
| 4.9 | 0,21 | 0,08 | 0,02 | Керамзитобетон – 0,2 | Полистирол -0,082 | Рубероид – 0,17 | |
| 4.10 | 0,55 | 0,03 | 0,04 | Древесина твердых пород – 0,2 | Стекловата – 0,05 | Стекловолокно – 0,036 | |
| 4.11 | 0,51 | 0,04 | 0,06 | Кирпич пустотелый – 0,44 | Войлок шерстяной – 0,045 | Гипс строительный – 0,35 | |
| 4.12 | 0,25 | 0,03 | 0,05 | Кирпич силикатный – 0,81 | Картон теплоизолированный БТК-1 – 0,04 | Древесина - доски – 0,15 | |
| 4.13 | 0,37 | 0,09 | 0,02 | Кирпич шлаковый – 0,58 | Вата минеральная легкая – 0,045 | Гудрон - 0,3 | |
| 4.14 | 0,51 | 0,06 | 0,05 | Кирпич силикатный – 0,81 | Каучук фторированный - 0,055 | ПВХ – 0,19 | |
| 4.15 | 0,45 | 0,04 | 0,03 | Бетон сплошной – 1,75 | Опилки - засыпка – 0,095 | Стекловолокно – 0,036 | |
| 4.16 | 0,26 | 0,07 | 0,02 | Бетон на каменном щебне – 1,3 | Стружки - набивка – 0,12 | Рубероид – 0,17 | |
| 4.17 | 0,23 | 0,03 | 0,05 | Бетон на песке – 0,7 | Ипорка (вспененная смола) - 0,038 | Пробковые листы легкие – 0,035 | |
| 4.18 | 0,48 | 0,05 | 0,02 | Пенобетон – 0,3 | Каучук натуральный – 0,042 | Штукатурка цементная – 0,9 | |
| 4.19 | 0,67 | 0,05 | 0,03 | Керамзитобетон – 0,2 | Гравий (наполнитель) – 0,93 | Битум – 0,47 | |
| 4.20 | 0,32 | 0,02 | 0,06 | Древесина твердых пород – 0,2 | Пенопласт ПХВ-1 – 0,05 | Штукатурка сухая – 0,21 |
Раздел 5. Действие магнитного поля на проводник с током
и движущийся заряд
5.1 Радиус кривизны траектории, по которой движется электрон в магнитном поле с индукцией В = 0,1 Тл, равен R = 0,5 см. Определить силу, действующую на электрон со стороны магнитного поля.
5.2 Прямой проводник с током I = 25 A расположен во внешнем однородном магнитном поле перпендикулярно силовым линиям. Какова индукция магнитного поля, если на каждый метр проводника со стороны поля действует сила 10 мН?
5.3 Заряд частицы, движущейся по окружности радиусом 5 см в магнитном поле со скоростью 2×105 м/с, в два раза больше элементарного заряда. Энергия этой частицы 10 кэВ. Определить индукцию магнитного поля.
5.4 Электрон, обладая скоростью v = 5×103 м/с влетает в однородное магнитное поле с индукцией В = 1 мТл перпендикулярно линиям магнитной индукции. Определить нормальное ап и тангенциальное аt ускорения электрона.
5.5 На проводник длиной ℓ = 10 см с током I = 12 А со стороны внешнего магнитного поля действует сила F = 1,6 мН. Определить индукцию магнитного поля, если угол между направлением тока и силовыми линиями поля a = 300.
5.6 Электрон движется в вакууме со скоростью v = 3×106 м/с в однородном магнитном поле с индукцией В = 0,1 Тл. Какова сила, действующая на электрон, если угол между направлением скорости и линиями магнитной индукции равен 900?
5.7 По горизонтально расположенному проводнику длиной ℓ = 20 см и массой т = 4 г течет ток 10 А. Проводник находится во внешнем магнитном поле такой величины и направления, что сила тяжести уравновешивается силой Ампера. Определить индукцию и направление внешнего магнитного поля.
5.8 Протон и a -частица влетают в однородное магнитное поле перпендикулярно линиям магнитной индукции. Сравнить радиусы окружностей, которые описывают частицы, если у них одинаковые скорости.
5.9 Электрон движется в однородном магнитном поле с магнитной индукцией В = 0,5 Тл по окружности. Сколько оборотов N сделает электрон за время t = 1 c?
5.10 Во сколько раз заряд частицы, движущейся со скоростью v = 106 м/с в магнитном поле с индукцией В = 0,3 Тл по окружности радиусом R = 4 см, больше элементарного электрического заряда? Энергия частицы W = 12 кэВ.
5.11 Два параллельных бесконечно длинных проводника с токами I 1 = I 2 находятся на расстоянии 2 см друг от друга и взаимодействуют с силой F = 1 мН на каждый метр их длины. Определить силу тока в проводниках.
5.12 Шины генератора представляют собой две параллельных металлических полосы длиной ℓ = 2 м каждая, отстоящие друг от друга на расстоянии d = 20 см. Определить силу F взаимного отталкивания шин в случае короткого замыкания, когда по ним протекает ток I = 10 кА.
5.13 Частица с зарядом q = 1,6×10-19 Кл движется в магнитном поле с индукцией В = 0,3 Тл по окружности радиусом R = 10 см со скоростью v = 20 м/с. Найти энергию частицы.
5.14 Два параллельных проводника длиной ℓ = 1 м каждый находятся на расстоянии d = 1 см друг от друга и взаимодействуют с силой F = 1 мН. Определить силу тока в проводах, если I 1 = I 2.
5.15 Ион, несущий один элементарный заряд, влетает в однородное магнитное поле с индукцией В = 0,2 Тл перпендикулярно линиям поля и движется по окружности радиусом R = 10 см. Определить момент импульса L иона.
5.16 Найти угловую скорость вращения электрона по окружности в магнитном поле с индукцией В = 0,02 Тл.
5.17 На заряженную частицу массой т = 9,1×10-31 кг, движущуюся по окружности радиусом R = 1 см в магнитном поле с индукцией В = 0,2 Тл действует сила F = 12,3 пН. Определить заряд частицы.
5.18 Нормальное ускорение a -частицы, движущейся в однородном магнитном поле равно ап = 2×1010 м/с2. Определить индукцию магнитного поля В, если скорость a -частицы v = 1,4 км/с.
5.19 Два параллельных проводника длиной ℓ = 5 м каждый расположены на расстоянии d = 10 см друг от друга. По проводникам пропускают одинаковые токи I 1 = I 2 = 30 А. Определить силу взаимодействия F проводников.
5.20 Протон, движущийся в однородном магнитном поле по окружности за 1 с делает N = 25×107 оборотов. Определить индукцию магнитного поля.
Раздел 6. Спектральные закономерности атома водорода
6.1 Найти наибольшую и наименьшую длину волны излучения, возникающего при переходе электрона в атоме водорода с пятого энергетического уровня в основное состояние (учесть возможность перехода через промежуточные уровни).
6.2 Спектр испускания водорода в видимом диапазоне содержит несколько спектральных линий. Какие переходы электрона в атоме водорода приводят к возникновению этих линий? Вычислить диапазон длин волн этих линий.
6.3 Найти наименьшую и наибольшую длины волн спектральных линий водорода в видимой области спектра.
6.4 Найти наибольшую длину волны в ультрафиолетовой области спектра водорода.
6.5 Какую наименьшую энергию (в электрон-вольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов спектр водорода имел три спектральных линии. Найти длину волны этих линий.
6.6 В каких пределах должны лежать длины волн монохроматического света, чтобы при возбуждении атома водорода квантами этого света наблюдалось три спектральных линии.
6.7 Рассчитать энергию и длину волны фотона, поглощение которого вызывает переход электрона в атоме водорода из основного состояния на второй энергетический уровень.
6.8 Рассчитать энергию и длину волны фотона, поглощение которого вызывает переход электрона в атоме водорода из основного состояния на пятый энергетический уровень.
6.9 Вычислить энергию и длину волны фотона, испускаемого однократно ионизированным атомом гелия при переходе электрона с третьего энергетического уровня на первый. К какой области спектра относится это излучение.
6.10 Электрон в атоме водорода находится на пятом энергетическом уровне. Чему равна его энергия. (Ответ выразить в электрон-вольтах) Излучение с какой длиной волны возникает при переходе этого электрона в основное состояние.
6.11 Определить длину волны излучения, возникающего при переходе электрона атома водорода с пятого энергетического уровня на третий. К какой области спектра относится это излучение.
6.12 Вычислить длину волны фотона, если излучение обусловлено переходом с четвертого энергетического уровня на основной. К какой области спектра относится это излучение.
6.13 Вычислить длину волны фотона, если излучение обусловлено переходом электрона в атоме водорода с третьего энергетического уровня на основной. К какой области спектра относится это излучение.
6.14 Определить длину волны излучения, возникающего при переходе электрона в атоме водорода со второго на основной энергетический уровень. К какой области спектра относится это излучение.
6.15 Рассчитать длину волны фотона, испускаемого при переходе электрона в атоме водорода с пятого на второй энергетический уровень. К какой области спектра относится это излучение.
6.16 Рассчитать длину волны фотона, испускаемого при переходе электрона в атоме водорода с четвертого на второй энергетический уровень. К какой области спектра относится это излучение.
6.17 Рассчитать длину волны фотона, испускаемого при переходе электрона в атоме водорода с третьего на второй энергетический уровень. К какой области спектра относится это излучение.
6.18 Вычислить энергию электрона, находящегося в атоме водорода в основном состоянии и на втором энергетическом уровне.
6.19 Вычислить энергию электрона, находящегося на третьем энергетическом уровне в атоме водорода. Излучение, с какой длиной волны может возникнуть при переходе электронов с третьего энергетического уровня в основное состояние.
6.20 Рассчитать энергию и длину волны фотона, поглощение которого вызывает переход электрона в атоме водорода из основного состояния на четвертый энергетический уровень.
Список рекомендуемой литературы
| 1. | Трофимова, Т.И. Курс физики: учеб. пособие для инженер.-техн. специальностей вузов / Т. И. Трофимова. - 18-е изд., стер. - М.: Академия, 2010. - 558 с. - (Высшее профессиональное образование). - ISBN 978-5-7695-7601-0: 451-00. |
| 2. | Детлаф, А.А. Курс физики: учеб. пособие для техн. вузов / А. А. Детлаф, Б. М. Яворский. - 8-е изд., стер. - М.: Академия, 2009. - 720 с. - (Высшее профессиональное образование). - ISBN 978-5-7695-6478-9: 495-00. |
| 3. | Трофимова, Т.И. Сборник задач по курсу физики с решениями: учеб. пособие для вузов / Т. И. Трофимова, З. Г. Павлова. - 7-е изд., стер. - М.: Высш. шк., 2006. - 591 с. - ISBN 5-06-004164-6: 349-00. |
| 4. | Чертов, А.Г. Задачник по физике: [учеб. пособие для втузов] / А. Г. Чертов, А. А. Воробьев. - 8-е изд., перераб. и доп. - М.: Физматлит, 2008. - 640 c. - ISBN 9875-94052-145-2: 501-00. |
| 5. | Физика. Физические основы механики. Молекулярная физика и термодинамика: методические указания к лабораторным работам для студентов и бакалавриата очной и заочной форм обучения / Е.А. Вощукова [и др.]; науч. ред. Е.А. Вощукова, С.П. Симохин; Брянск. гос. инженерно-технол. акад. – 4-е изд., перераб. и доп. – БГИТА, 2011. – 113 с. |
| 6. | Физика. Электромагнетизм. Колебания и волны: Методические указания к лабораторным работам для студентов бакалавриата очной и заочной форм обучения. Издание 4-е, переработанное и дополненное / Брянская гос. инженерно-технологическая академия; Сост. Э.В. Бабкова, Е.А. Вощукова, Ю.А. Ивашкин и др. - Брянск, БГИТА, 2011. - 62 с. |
| 7. | Физика. Физика твердого тела. Атомная и ядерная физика: Методические указания к лабораторным работам для студентов бакалавриата очной и заочной форм обучения. Издание 4-е, переработанное и дополненное / Брянская гос. инженерно-технологическая академия; Сост. Е.А. Вощукова, К.Н. Евтюхов, Ю.А. Ивашкин и др. - Брянск, БГИТА, 2011. - 81 с. |
| 8. | Механика: сборник методических указаний для самостоятельной работы студентов БГИТА дневного и заочного обучения/ М.Д. Преженцев; Брянск. гос. инженерно-технол. акад. - БГИТА, 2005. – 66 с. |
| 9. | Молекулярная физика и термодинамика: сборник методических указаний для самостоятельной работы студентов БГИТА дневного и заочного обучения/ В.А. Матанцева, Л.М. Притыченко; Брянск. гос. инженерно-технол. акад. - БГИТА, 2005 – 33 с. |
| 10. | Физика. Электромагнетизм: сборник методических указаний для самостоятельной работы студентов БГИТА дневного и заочного обучения/ С.П. Симохин, Т.И. Ушакова; Брянск. гос. инженерно-технол. акад. - БГИТА, 2005. – 46 с. |
| 11. | Квантовая физика: Методические указания к самостоятельному изучению квантовой физики студентами инженерно-технических специальностей/ Брянск. гос. технол. акад. Сост. Ю.Г. Сахаров, Э.В Бабкова. - Брянск, 2006. - 108 с. |
| 12. | Сборник методических указаний для самостоятельной работы студентов очной и заочной форм обучения по теме «Физика твердого тела (структура и тепловые свойства кристаллов)». Брянск, гос. инж. -технол. акад. Сост. Г. В. Егоров. - Брянск: БГИТА, 2010. - 34с. |
| 13. | Сборник методических указаний для самостоятельной работы студентов бакалавриата очной и заочной форм обучения по теме «Физика элементарных частиц». Брянск, гос. инж. -технол. акад. / С.П. Симохин. - Брянск: БГИТА, 2011. – 32 с. |
Ивашкин Юрий Александрович
Бабкова Элеонора Васильевна
Матанцева Вера Анатольевна
Симохин Сергей Пертрович
|
|
|
|
|
Дата добавления: 2015-05-07; Просмотров: 1312; Нарушение авторских прав?; Мы поможем в написании вашей работы!