Деформація кручення

Деформація зсуву

Зсувом називають таку деформацію тіла, коли його плоскі шари зміщуються паралельно один одному (мал. 1.3б). Зсув виникає під дією дотичного напруження:

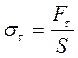(1.6)

Відповідно до закону Гука 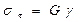, де G - модуль зсуву, - кут зсуву, що зветься також відносним зсувом (ΔX = СС' - абсолютний зсув, який дорівнює зсуву одного шару відносно іншого, a CD - відстань між цими шарами).

Деформація кручення виникає у зразку, коли один його переріз нерухомий, а в іншому діє пара сил, момент якої спрямований вздовж осі зразка (мал. З.Зв). Ця деформація використовується в крутильних терезах.

Для кожного з розглянутих типів деформацій спостері­гаються у межах пружної реакції зразка прямо пропорційні залежності між напруженням та відносною деформацією. Коефіцієнти пропорційності - модулі пружності - можна виразити через модуль Юнга (Е) та коефіцієнт Пуассона (и) матеріалу, тобто для пружних деформацій ізотропних тіл Е та μ повністю визначають реакцію зразка на прикладені на­пруження. Наприклад, модуль об'ємної пружності тонкої стінки судини можна подати у вигляді

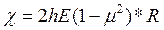, (1.7)

де h і R - товщина стінки та радіус судини відповідно, h<< R.

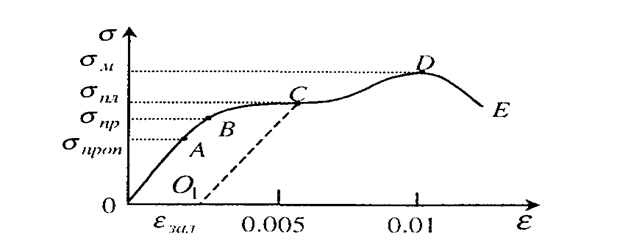
Мал. 1.4. Діаграма розтягу для сталі.

Експериментальне отриману при деформації залежність напруження, що виникає у зразку, від відносної деформації називають діаграмою деформації. Типовий вигляд діаграми розтягу металевого зразка подано на мал. 1.4.

Наведену криву можна умовно поділити на п'ять зон. Зона ОА має назву зони пропорційності. У межах цієї зони виконується закон Гука. Зона ОB - це зона пружності, де після зняття напруження тіло відновлює свої розміри і форму. Зона ВС зветься зоною загальної плинності. У цій зоні подовження зразка відбувається без помітного збіль­шення напруження. Зона CD - це зона зміцнення, у цій зоні подовження зразка супроводжується зростанням напружен­ня, на зразкові з'являється місце майбутнього розриву — шийка, формування якої (точка D) супроводжується проце­сом місцевої плинності в зоні DE і розривом зразка. Якщо зменшувати навантаження у зоні ВС, то відповідний графік σ= f (ε) піде паралельно ОА і перетне вісь абсцис у деякій точці О_|. Відрізок ОО_| визначає залишкову деформацію ε _зал, що характеризує пластичну деформацію зразка. Отримання діаграми деформації дозволяє визначити ряд найважливі­ших характерних точок і відповідних їм величин:

· межа пропорційності σ _проп - найбільше напруження, при якому ще виконується закон Гука;

· межа пружності σ _пр - найбільше напруження, при якому немає залишкових деформацій;

· межа плинності σ _пл- найбільше напруження, при якому відбувається зростання деформації без помітного збільшен­ня напруження;

· межа міцності σ _м - найбільше напруження, яке може витримати зразок.

При деформаціях тіл часто виявляються в'язко-пружні властивості, які полягають у тому, що напруження залежить не лише від деформації (ε), а й від швидкості її зміни з ча­сом, тобто похідної ε '.

Дата добавления: 2015-05-24