Виведення розрахункових формул. Маятник Максвелла, піднятий на деяку висоту h, має потенціальну енерґію mgh

Маятник Максвелла, піднятий на деяку висоту h, має потенціальну енерґію mgh. Якщо маятник з такого положення відпустити, то він, опускаючись вниз, здійснює складний поступально-обертальний (плоский) рух. Під час руху вниз потенціальна енерґія маятника зменшується і перетворюється у кінетичну енерґію поступального руху 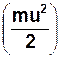, кінетичну енерґію обертального руху та в роботу проти сил тертя. Якщо тертям знехтувати, то згідно з законом збереження енерґії

. (1)

Знаючи кінцеву лінійну швидкість u точок ободу валу маятника та кінцеву кутову швидкість можна з формули (1) визначити момент інерції маятника Максвелла.

Лінійну швидкість u точок ободу валу маятника можна визначити, знаючи висоту h, на яку піднятий маятник, і час t опускання його з цієї висоти

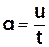; . (2)

Виключивши з рівнянь (2) лінійне прискорення α, з яким опускається маятник, отримаємо:

. (3) Лінійна швидкість u точок ободу валу маятника, його кутова швидкість і радіус R зв’язані між собою співвідношенням

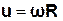. (4)

На основі (3) і (4) одержимо:

, (5)

де d₀ – діаметр валу маятника.

Підставляючи значення u з (3) і із (5) у формулу (1), отримаємо для моменту інерції маятника Максвелла:

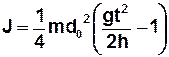. (6)

Врахувавши, що загальна маса маятника m = m₀ + m_M + m_K,

де m₀ – маса валу маятника;

m_M – маса маховика;

m_K – маса допоміжного кільця, одержимо:

. (7) Момент інерції маятника Максвелла, як тіла правильної ґеометричної форми, можна також обчислити теоретично за формулою:

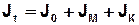, (8)

де J₀ – момент інерції валу маятника,

J_M – момент інерції маховика,

J_K – момент інерції допоміжного кільця.

Значення моментів інерції окремих складових маятника визначаються за формулами:

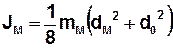; ; . (9)

Отже:

, (10)

де d_M – зовнішній діаметр маховика;

d_K – зовнішній діаметр допоміжного кільця.

При підготовці до виконання роботи використати:

Дата добавления: 2015-05-24