Основи кореляційного аналізу

п.1. Типи зв’язків між випадковими величинами. На практиці часто потрібно встановити і оцінити залежність досліджуваної випадкової величини від однієї або декількох інших випадкових величин.

Випадкові величини можуть бути пов’язані функціональною або статистичною залежністю чи бути незалежними.

Функціональна залежність, при якій кожному можливому значенню поставлено у відповідність за певним правилом (законом) одне значення , між двома випадковими величинами зустрічається дуже рідко, оскільки обидві величини або одна з них зазнають впливу випадкових факторів. В тих випадках, коли зв’язок між випадковими величинами втрачає функціональний характер і досліджуваний об’єкт (чи система об’єктів) переходить не в однозначно визначений стан, а в один із можливих станів, мова може йти тільки про так званий стохастичний зв’язок. Цей зв’язок між випадковими величинами полягає в тому, що одна з них реагує на зміну іншої зміною свого закону розподілу.

В практиці статистичних досліджень часто розглядається частковий випадок стохастичного зв’язку, який називається статистичним зв’язком. Дві випадкові величини, задані статистичними розподілами, називають статистично залежними, якщо зміна розподілу однієї з них змінює статистичний розподіл іншої.

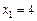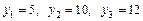Нехай вивчається зв’язок між випадковими величинами та і встановлено, наприклад, що при появі значення випадкової величини величина набуває значень . Середнє арифметичне цих чисел називають умовним середнім і позначають . В загальному випадку, умовним середнім 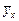називається середнє арифметичне значень випадкової величини , що відповідають значенню випадкової величини . 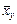Аналогічно визначається і умовне середнє значень випадкової величини , що відповідають значенню випадкової величини . 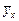Якщо умовне середнє значень випадкової величини є функцією 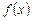відповідних значень величини , то залежність від називається кореляційною. Рівняння називається рівнянням регресії на , функція 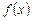– регресією на , а її графік – лінією регресії на . Аналогічно визначають кореляційну залежність від і рівняння регресії . 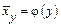Якщо обидві регресі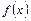ї і – лінійні функції, тобто , то кореляційна залежність між величинами і називається лінійною кореляцією. Очевидно, в цьому випадку обидві лінії регресії будуть прямими. Якщо графіком регресії 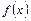чи регресії є деяка крива, то таку кореляцію називають криволінійною.

п.2. Визначення параметрів рівняння лінійної регресії за методом найменших квадратів. Однією із задач теорії кореляції є встановлення форми кореляційної залежності однієї величини від іншої , тобто знаходження регресії на . Поряд з цим досліджується можливість знаходження міри такої залежності з допомогою чисел.

Нехай між та існує лінійна кореляційна залежність і для знаходження параметрів рівняння прямої лінії регресії проведено 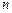незалежних спостережень, результати яких подані в таблиці10.1.

Таблиця 1

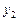
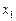
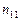
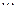
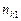
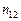
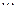
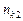
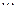
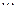
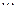
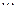
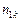
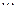
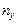
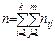
Будемо шукати регресію на у вигляді:

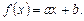(10.1)

Для визначення параметрів і скористаємось методом найменших квадратів, згідно з яким і вибирають таким чином, щоб сума квадратів відхилень умовних середніх 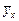від значень була найменшою. Отже, необхідно знайти такі значення , , за яких функція:

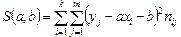(10.2)

досягає мінімуму. Враховуючи необхідну умову екстремуму для визначення і , дістанемо систему рівнянь:

(10.3)

Враховуючи те, що

де – вибіркові середні величин та , друге рівняння системи (10.3) набуде вигляду , звідки

Підставляючи значення в перше рівняння системи (10.3), отримаємо:

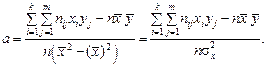(10.4)

Параметр називається вибірковим коефіцієнтом регресії на і позначається . Тоді вибіркове рівняння прямої лінії регресії на матиме вигляд:

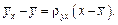(10.5)

Вибіркове рівняння прямої лінії регресії на можна записати ще й так:

, (10.6)

де вибірковий коефіцієнт кореляції:

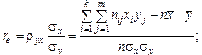(10.7)

тут – вибіркові середні квадратичні відхилення та .

Вибірковий коефіцієнт кореляції має властивості:

1) абсолютна величина вибіркового коефіцієнта кореляції не перевищує одиниці, тобто ;

2) якщо вибірковий коефіцієнт кореляції дорівнює нулю і вибірковими лініями регресії є прямі, то і не зв’язані лінійною кореляційною залежністю;

3) якщо абсолютна величина вибіркового коефіцієнта кореляції дорівнює одиниці, то випадкові величини і зв’язані лінійною функціональною залежністю;

4) із зростанням абсолютної величини вибіркового коефіцієнта кореляції лінійна кореляційна залежність стає більш тісною і при переходить у функціональну залежність.

Приклад 1. Вибірка із генеральної сукупності двовимірного випадкового вектора подана у вигляді таблиці 2. За даними цієї таблиці знайти вибіркове рівняння прямої лінії регресії на .

Таблиця 2

		–	–	–	–
			–	–	–
	–				–
	–	–
	–	–
	–	–	–	–

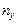
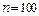
Розв’язання. Щоб записати вибіркове рівняння прямої лінії регресії на (10.6) треба знати вибіркові середні 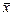та 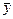компонент та , їх вибіркові середні квадратичні відхилення та вибірковий коефіцієнт кореляції 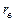. Маємо:

;

;

;

;

.

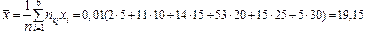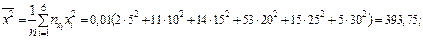
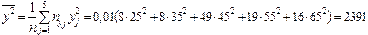Щоб визначити вибірковий коефіцієнт кореляції за формулою (10.7), обчислимо :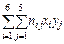

.

Тоді,

.

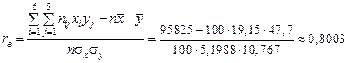Підставивши знайдені значення у формулу (10.6), отримаємо вибіркове рівняння прямої лінії регресії на :

або .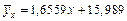

Дата добавления: 2015-05-24