Теорема Штейнера

Розглянемо приклади розрахунку моментів інерції найпростіших тіл.

Момент інерції суцільного диска. Розглянемообертання диска масою m і радіусом R відносно осі, яка проходить через центр мас диска, перпендикулярно до його площини, як це показано на рис. 4.2.

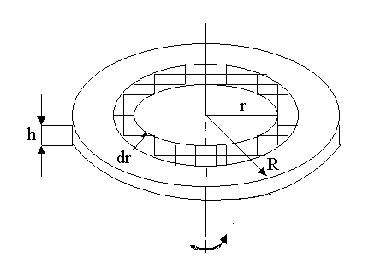
Рис. 4.2

Момент інерції заштрихованої частини диска з масою dm і радіусом r у відповідності з (4.1.3) буде дорівнювати

. (4.2.1)

Маса заштрихованої частини диска дорівнює

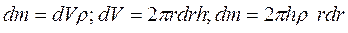. (4.2.2)

Елемент маси dm (4.2.2) підставимо в (4.2.1) і інтегруємо по радіусу диска

,

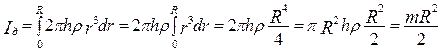де h – товщина диска; r - густина речовини диска.

Таким чином момент інерції диска відносно осі обертання, перпендикулярної до площини диска, дорівнює

I _{д =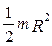} . (4.2.3)

Момент інерції стержня відносно осі обертання, яка проходить через кінець стержня, перпендикулярно до його довжини.

Маса стержня m, а довжина l (рис.4.3).

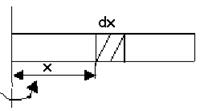
Рис. 4.3

Для знаходження моменту інерції стержня скористаємося формулою (4.2.1)

dI=dmx² ,

де dm=Sdxr - маса виділеного елемента; S – переріз стержня; r - густина речовини стержня; dx – довжина виділеного елемента стержня.

Інтегруємо цей вираз по довжині стержня, одержимо

. (4.2.4)

Таким чином знайдена величина моменту інерції стержня відносно осі, яка проходить через кінець стержня, перпендикулярно до його довжини, буде дорівнювати

.

Момент інерції стержня відносно осі, яка проходить через центр мас, перпендикулярно до його середини (рис.4.3)

Рис.4.4

Момент інерції безмежно малого елемента стержня відносно осі, показаної на рисунку, дорівнює

dI=dm x²,

де dm = Sdxr - маса заштрихованого елемента.

З урахуванням цієї маси момент інерції елемента стержня буде дорівнювати

dI= Srx² dx. (4.2.5)

Інтегруємо вираз (4.2.5) в межах від 0 до 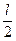, помноживши попередньо весь результат на 2 (дві симетричні частини стержня)

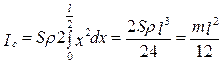. (4.2.5)

Таким чином момент інерції стержня відносно осі, яка проходить через його центр мас (рис.4.4), дорівнює

.

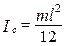Момент інерції кулі знайдемо відповідно до рис. 4.5.

Рис.4.5

Заштрихована частина кулі має форму диска радіусом у і товщиною dz.

Момент інерції виділеного диска відповідно до (4.2.3) дорівнює

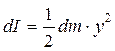, (4.2.6)

Маса виділеного диска радіусом у і товщиною dz буде дорівнювати

dm= py²rdz. (4.2.7)

Підставимо (4.2.7) у (4.2.6), одержимо

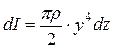. (4.2.8)

З рис.4.5 видно, що y²=R²-z², тому

dI = 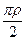[R²-z²] ²dz = 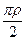[R⁴-2R²z²+z⁴]dz = 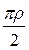[ R⁴ dz -2R²z²dz +Z⁴ dz ].

Інтегруємо цей вираз в межах z від 0 до R, урахувавши нижню частину кулі, не показану на рис. 4.5

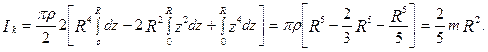
Тобто момент інерції кулі масою m і радіусом R дорівнює

І_к = . (4.2.9)

У деяких випадках момент інерції твердого тіла відносно осі, яка не збігається з центром мас тіла, розраховують за теоремою Штейнера.

Момент інерції тіла І відносно довільної осі ОО₁ дорівнює сумі моменту інерції цього тіла відносно паралельної осі І_с, яка проходить через центр мас, і добутку маси цього тіла на квадрат відстані між паралельними осями (рис. 4.6).

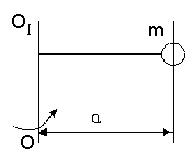
Рис. 4.6

I = I_c + ma², (4.2.10)

де вираз (4.2.10) є теоремою Штейнера.

Покажемо справедливість цієї теореми на прикладі розрахунку моментів інерції стержня, для якого І_с = 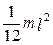(рис. 4.7).

Рис. 4.7

,

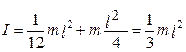що підтверджується попереднім незалежним виведенням методом інтегрування.

Моменти інерції найпростіших тіл показані в таблиці 1.

Таблиця 1

Тіло	Вісь обертання	Момент інерції
Обруч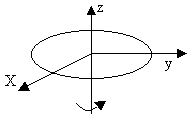
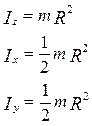
Диск
Стрижень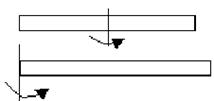
Куля

4.3. Момент імпульсу. Момент сили. Основне рівняння динаміки обертального руху. Кінетична енергія обертання

Моментом імпульсу матеріальної точки масою m_i називається векторний добуток радіуса-вектора 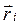на вектор імпульсу 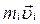цієї точки

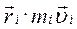= [ ]. (4.3.1)

За означенням напрям вектора моменту імпульсу визначають за правилом векторного добутку. На рис. 4.7 показано напрям вектора моменту імпульсу матеріальної точки, який збігається з напрямком поступального руху правого гвинта.

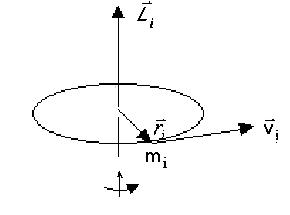
Рис.4.7

Момент імпульсу твердого тіла знаходять за допомогою додавання моментів імпульсу всіх матеріальних точок тіла:

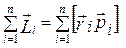, (4.3.2)

або

. (4.3.3)

Знайдемо похідну за часом від рівняння (4.3.1)

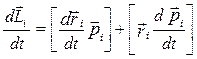, (4.3.4)

де 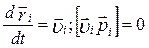, так як це однонапрямлені вектори;

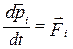- сила у відповідності з другим законом Ньютона; - момент сили, діючий на і-ту матеріальну точку.

З урахуванням всіх позначень рівність (4.3.4) набуває вигляду

. (4.3.5)

Підсумувавши цю рівність для всіх матеріальних точок твердого тіла, одержимо

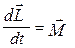. (4.3.6)

Рівність (4.3.3) для твердого тіла дає величину моменту імпульсу тіла, який дорівнює

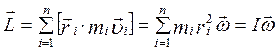. (4.3.7)

Таким чином для твердого тіла виконується рівність

,

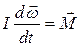або (4.3.8)

.

Рівності (4.3.8) у фізиці називають основним рівнянням динаміки обертального руху. В цих рівностях І – скалярна величина, яка є мірою інертності тіл при обертальному русі; 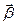- кутове прискорення – векторна величина, напрям якого збігається з напрямком поступального руху правого гвинта. Вектор моменту імпульсу 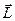направлений за напрямком вектора кутового прискорення.

Основне рівняння динаміки обертального руху відіграє таку ж роль у динаміці обертального руху, що і другий закон Ньютона для поступального руху. Ці закони мають також однакову форму написання.

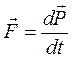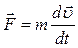, або , або 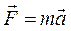. (4.3.9)

, або , або 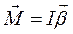. (4.3.10)

Знайдемо вираз для кінетичної енергії обертального руху матеріальної точки або твердого тіла.

Скористаємося формулою кінетичної енергії поступального руху матеріальної точки або твердого тіла:

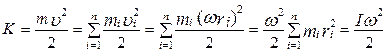. (4.3.11)

де 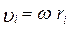; - момент інерції твердого тіла відносно осі обертання.

Якщо тіло здійснює поступальний і обертальний рухи, то його повна кінетична енергія буде дорівнювати сумі кінетичних енергій поступального й обертального рухів

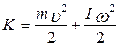, (4.3.12)

де І – момент інерції тіла відносно вибраної осі обертання; u – швид-кість руху центра мас цього тіла.

Зіставивши вирази кінетичної енергії поступального й обертального рухів, робимо висновок, що мірою інертності при обертальному русі є момент інерції тіла.

Розглянемо рух матеріальної точки або твердого тіла по коловій траєкторії у відповідності з рис. 4.8.

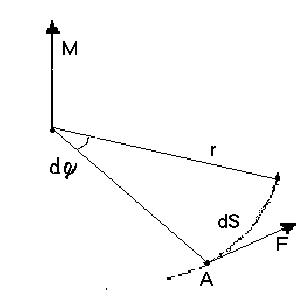
Рис. 4.8

За безмежно малий час матеріальна точка під дією сили F здійснює переміщення по дузі dS, довжина якої дорівнює rdj. При цьому виконується механічна робота

dA = FdS = Fr dj = M dj. (4.3.13)

Потужність у цьому випадку буде дорівнювати

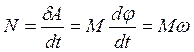, (4.3.14)

де М – момент діючої сили; w - кутова швидкість.

Потужність є скалярною величиною, тому

. (4.3.15)

4.4. Закон збереження моменту імпульсу і його використання. Гіроскопи. Гіроскопічний ефект

Скористаємось основним рівнянням динаміки обертального руху (4.3.6)

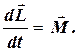(4.4.1)

Якщо система замкнута, то будь-які зовнішні сили будуть відсутні. Це означає, що 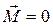. Тому для замкнутої системи виконується рівність

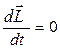. (4.4.2)

Рівність (4.4.2) має місце лише в одному випадку: коли результуючий момент імпульсу дорівнює сталій величині, тобто

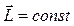. (4.4.3)

В будь-якій замкнутій системі сумарний момент імпульсу всіх тіл цієї системи з часом не змінюється. Це і є формулювання закону збереження моменту імпульсу. Закон збереження моменту імпульсу має досить широке використання.

Оскільки

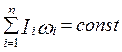, (4.4.4)

то зміна моменту інерції І_і приводить до відповідної зміни кутової швидкості. Приклади використання закону збереження моменту імпульсу мають місце в техніці (наприклад регулятор Уатта), в спорті (фігурне катання) тощо.

Масивні симетричні тіла, які обертаються з великою кутовою швидкістю, називаються гіроскопами.

Якщо до гіроскопа, який здійснює обертальний рух прикласти дві сили, які намагаються повернути його навколо осі, перпендикулярної до осі обертання, то гіроскоп повернеться відносно третьої осі, перпендикулярної до перших двох осей. Цю властивість гіроскопа називають гіроскопічним ефектом (рис.4.9).

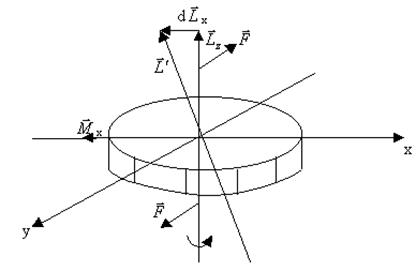
Рис.4.9

Дія пари сил 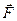призводить до повертання гіроскопа відносно осі х. Напрям моменту сил 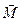_x збігається з віссю х.

У відповідності з основним рівнянням динаміки обертального руху виникає додатковий момент імпульсу 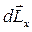, тобто

.

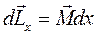Вісь обертання гіроскопа z повернеться і займе нове положення вздовж рівнодійної векторів 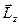і . Це рівноцінно тому, що гіроскоп повертається відносно осі y.

Сучасні гіроскопи широко використовуються у техніці. Обертаю-чись з кутовою швидкістю у сотні тисяч обертів за хвилину, гіроскопи допомагають прокладати курс різноманітним плавзасобам, стабілізують польоти ракет тощо.

ЛЕКЦІЯ 5

Елементи спеціальної теорії відносності

5.1. Постулати спеціальної теорії відносності. Перетворення координат Лоренца.

5.2. Наслідки перетворення координат Лоренца. Закон складання швидкостей.

5.3. Зв’язок маси й енергії.

5.1. Постулати спеціальної теорії відносності

Дата добавления: 2015-05-24