Практичне заняття 14. Оцінка ступеню участі міст у формуванні сусідських зв’язків із застосуванням теорії графів

І. Завдання:

познайомитися с основами теорії графів; познайомитися с основами теорії графів; вивчити способи використання теорії графів для кількісного аналізу суспільно-географічного положення; розглянути використання теорії графів в оцінці ролі міст у системі зв’язків першого, другого тощо порядку; навчитися будувати графи, матрицю суміжностей графа; навчитися обчислювати ступінь участі вершин графа у формуванні зв’язків різних порядків; навчитися підраховувати діаметр графу.

Теоретичні засади та порядок виконання роботи:

відношення географічного положення допускають просту й ефективну формалізацію у вигляді так званих графів. Множину географічних об'єктив — міст, регіонів, країн — показують точками (вершини графа), а відношення між ними — потоки вантажів і пасажирів, товарів, енергії, фінансів, інформації, управління — представляють лініями (ребра або дуги графа). Спеціальний розділ математики — теорія графів — дозволяє обчислити для графа різноманітні параметри, що характеризують участь вершин і ребер у різноманітних зв'язках і відношеннях.

Розглянемо приклад. На рисунку показаний граф, що формалізує мережу залізниць між містами: 1. Севастополь, 2. Сімферополь, 3. Херсон, 4. Запоріжжя, 5. Миколаїв, 6. Дніпропетровськ, 7. Кіровоград, 8. Черкаси. Вже візуально можна помітити, що одні міста (вершини) розміщені більш "центрально", а інші — більш "периферійно". Спробуємо таку різницю виразити в числах, кількісно. Необхідно звернути увагу нате, що такий аналіз не потребує реальних віддалей пропускної здатності доріг, вантажо- чи пасажиропотоків. Основою обчислень виступає наявність-відсутність зв'язків, і тільки. Одиниця обчислень - ребро графа, тобто лінія між двома його вершинами. Це безрозмірна або топологічна одиниця, що немає метричного виміру.

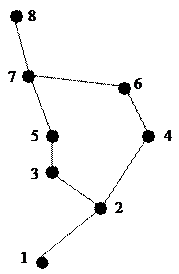
Проаналізуємо матрицю суміжностей графа // С //.

									S

Її елементи - одиниці - показують наявність безпосереднього сусідства (сусідства першого порядку) між відповідними парами вершин. За цією матрицею можна оцінити роль вершин у системі зв'язків першого порядку: лідери - вершини 2 та 7, які мають трьох сусідів; вершини 3, 4, 5, 6 мають по два сусіди, вершини 1 і 8 - по одному сусіду. Можна обчислити частки, які припадають на кожну вершину (місто) у формуванні зв'язків першого порядку.

Розглянемо матрицю суміжностей другого ступеня // С² //.

Діагональні елементи цієї матриці (з лівого верхнього кута у правий нижній) показують для кожної вершини кількість її безпосередніх сусідів - зв'язків першого порядку. Всі інші (недіагональні) елементи називають для кожної пари вершин число зв'язків другого порядку (з віддалями у 2 ребра). За цією матрицею у кожної вершини можна обчислити її участь у зв'язках першого і другого порядку за сумою таких зв'язків або ж за їх часткою по відношенню до загальної суми зв'язків всіх міст.

									S

Аналогічно можна оцінити участь вершин у зв'язках третього (// С³ //), четвертого (// С⁴ //) і наступних порядків аж до діаметра графа, що являє собою найкоротшу віддаль між двома найбільш віддаленими вершинами. У нашому прикладі діаметр графа дорівнює 5, оскільки це найкоротша віддаль між найбільш віддаленими вершинами 1 - 8 (див. матрицю // L //).

ІІ. Завдання для самостійного виконання студентами (за картосхемою мережі залізниць України, див. Додаток):

Варіант 1

1. Накресліть граф транспортної мережі, що формалізує мережу залізниць між містами: 1. Київ, 2. Житомир, 3. Чернігів, 4. Суми, 5. Харків, 6. Полтава

2. Побудуйте відповідну матрицю суміжностей першого ступеню.

3. Підрахуйте саму зв’язків першого порядку, які припадають на кожну вершину.

4. Побудуйте матрицю суміжностей другого ступеня.

5. Підрахуйте саму зв’язків першого і другого порядку, які припадають на кожну вершину.

6. Обчисліть загальну суму зв’язків першого і другого порядку для всіх вершин. Чому дорівнює діаметр графу?

7. За сумою зв’язків для кожної вершини обчисліть частку кожної з них у формуванні зв’язків першого і другого порядку.

8. Зробить висновки, давши інтерпретацію отриманим результатам.

Варіант 2

1. Накресліть граф транспортної мережі, що формалізує мережу залізниць між містами: 1. Ужгород, 2. Львів, 3. Тернопіль, 4. Хмельницький, 5. Чернівці, 6. Івано-Франківськ

2. Побудуйте відповідну матрицю суміжностей першого ступеню.

3. Підрахуйте саму зв’язків першого порядку, які припадають на кожну вершину.

4. Побудуйте матрицю суміжностей другого ступеня.

5. Підрахуйте саму зв’язків першого і другого порядку, які припадають на кожну вершину.

6. Обчисліть загальну суму зв’язків першого і другого порядку для всіх вершин. Чому дорівнює діаметр графу?

7. За сумою зв’язків для кожної вершини обчисліть частку кожної з них у формуванні зв’язків першого і другого порядку.

8. Зробить висновки, давши інтерпретацію отриманим результатам.

Варіант 3

1. Накресліть граф транспортної мережі, що формалізує мережу залізниць між містами: 1. Луганськ, 2. Донецьк, 3. Харків, 4. Полтава, 5. Дніпропетровськ, 6. Запоріжжя

2. Побудуйте відповідну матрицю суміжностей першого ступеню.

3. Підрахуйте саму зв’язків першого порядку, які припадають на кожну вершину.

4. Побудуйте матрицю суміжностей другого ступеня.

5. Підрахуйте саму зв’язків першого і другого порядку, які припадають на кожну вершину.

6. Обчисліть загальну суму зв’язків першого і другого порядку для всіх вершин. Чому дорівнює діаметр графу?

7. За сумою зв’язків для кожної вершини обчисліть частку кожної з них у формуванні зв’язків першого і другого порядку.

8. Зробить висновки, давши інтерпретацію отриманим результатам.

Рекомендована література:

1. Березина Л. Ю. Графы и их применение: Пособие для учителей – М., 1979.

2. Голиков А. П., Трофимов А. М., Черванёв И. Г. Математические методы в географии – Х, 1986.

3. Михеева В. С. Математические методы в экономической географии. Ч. 2. Приложение теории графов: Курс лекций – М., 1983.

4. Топчієв О. Г. Основи суспільної географії – Одеса, 2001.

Дата добавления: 2015-05-24