Лабораторна робота № 2.2

Визначення в’язкості повітря капілярним методом

Мета роботи: визначити в’язкість повітря.

Теоретичні відомості

(Теорія до даної роботи описана в лекційному курсі (інтерактивного комплексу Ч І) §2.18-2.20)

Молекули газів та рідин внаслідок теплового руху безперервно і хаотично рухаються. При цьому вони обмінюються імпульсами та енергіями. Якщо в середовищі існує просторова неоднорідність густини, температури або швидкості впорядкованого руху окремих шарів, то на тепловий рух молекул накладається впорядкований рух, який веде до вирівнювання цих неоднорідностей.

Явища переносу – це процеси встановлення рівноваги в системі шляхом переносу маси (дифузія), енергії (теплопровідність) та імпульсу напрямленого руху (внутрішнє тертя або в’язкість).

Явище дифузії полягає у взаємному проникненні і перемішуванні частинок речовини внаслідок неоднорідності густини чи різниці концентрацій компонент суміші в різних місцях об’єму. Потік маси виникає в напрямку зменшення густини чи концентрації. Явище описується емпіричним законом Фіка ,

де D – дифузія, яка дорівнює масі речовини, що переноситься через одиницю площі за одиницю часу при одиничному градієнті густини; – градієнт густини; S – площа поверхні; dt – час переносу.

Якщо вдовж осі Z існує градієнт температури 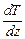, то в напрямку зменшення температури виникає потік тепла через поверхню площею dS перпендикулярну до осі Х. Явище теплопровідністі описує закон Фур’є ,

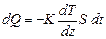де dQ – кількість теплоти; dt – проміжок часу; К – теплопровідність речовини – це кількість теплоти, що проходить за одиницю часу через одиничну площу при одиничному градієнті густини. Механізм явища теплопровідністі полягає в передачі енергії теплового хаотичного руху при зіткненні молекул.

У явищі внутрішнього тертя (в’язкості) спостерігається перенос імпульсу напрямленого руху із шарів, які рухаються швидше до повільніших і навпаки. У результаті хаотичного теплового руху молекули безперервно і хаотично переходять із шару в шар (рис.1) і при зіткненні з іншими молекулами обмінюються імпульсами впорядкованого руху (). При переході із шару А, який рухається із більшою швидкістю в шар В,який рухається із меншою швидкістю, молекули переносять у другий шар свій імпульс впорядкованого руху, а у більш швидкий шар переходять молекули з меншим імпульсом. У результаті більш швидкий шар гальмується, менш швидкий прискорюється. Такий процес з механічної точки зору можна пояснити виникненням сил тертя, які сповільнюють більш швидкий і прискорюють повільніший шари молекул. Ці сили напрямленні по дотичній до поверхні стичних шарів проти відносної швидкості. Дослід показує, що імпульс руху dp, що передається із шару в шар через поверхнюпропорційний градієнту швидкості шарів, площі цієї поверхні S та часу переносу dt

. (1)

В результаті між шарами виникає сила внутрішнього тертя

, (2)

де h – в’язкість середовища. Із співвідношення (2) визначимо

,

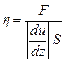тобто в’язкість η - чисельно дорівнює силі внутрішнього тертя, яка діє між шарами одиничної площі при одиничному градієнті швидкості. В’язкості h залежить від природи речовини і її стану.

В системі СІ .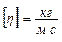

Для ідеального газу, згідно молекулярно-кінетичної теорії

, (3)

де r –густина газу; – середня довжина вільного пробігу молекул, це відстань, яку проходь молекула за час між двома послідовними зіткненнями; ‑середня арифметична швидкість теплового руху молекул.

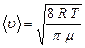, (4)

де m – молекулярна маса газу; R – універсальна газова стала; Т – температура.

Для визначення в’язкості розглянемо метод Пуазейля. За цим методом в’язкість визначають вимірюючи швидкість витікання певного об’єму середовища через капіляр.

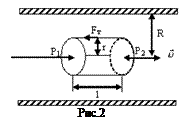Виділимо в капілярі уявний циліндричний об’єм газу радіусом r і довжиною l, як показано на рис.2.

Позначимо тиски на його торцях і . При усталеній течії сила тиску на циліндр урівноважується силою внутрішнього тертя 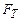, яка діє на бічну поверхню циліндра з боку зовнішніх шарів газу:

(5)

Сила внутрішнього тертя визначається за законом Ньютона (2).

Зважаючи на те, що S = 2πrl і швидкість u (r) зменшується при віддаленні від осі труби, тобто ,то можна записати

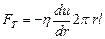. (6)

В цьому випадку умова стаціонарності запишеться у вигляді:

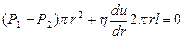. (7)

Інтегруючи цю нерівність одержимо:

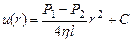, (8)

де С – стала інтегрування, яка визначається граничними умовами задачі.

При r = R швидкість газу повинна перетворитися на нуль. Тоді остаточно одержимо

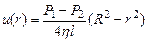. (9)

Підрахуємо об’ємну витрату газу Q, тобто об’єм газу, що протікає за одиницю часу через поперечний переріз капіляра. Через кільцеву площу з внутрішнім радіусом r і зовнішнім r + dr, щосекунди протікає об’єм газу

(10)

Враховуючи (9) після інтегрування отримаємо

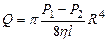. (11)

Формулу Пуазейля (11), можна використати для експериментального визначення в’язкості газу.

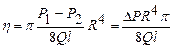, (12)

де ∆ Р = 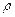g ∆ h -–різниця тисків, яка вимірюється за допомогою рідинного манометра; 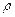– густина рідини в манометрі; g – прискорення вільного падіння; ∆ h – різниця рівнів води в манометрі

. (13)

Формулу Пуазейля (11) було одержано в припущенні ламінарної течії газу та рідини. Ця формула справедлива для ділянки капіляра, в якій встановилась стала течія з законом розподілу швидкостей (9) по перерізу труби. Така течія встановлюється на деякій відставні від входу в капіляр, тому для досягнення достатньої точності експерименту необхідне викона­ння умови R << L, де R – радіус, L – довжина капіляра.

Дата добавления: 2015-05-24