Краткая теория

Движение частицы под действием постоянной силы

Редакторы Г.А. Клебче, Л.Н. Вылегжанина

Георгий Иванович Рузавин

Учебник

КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ

Корректор К.В. Федорова

Оформление художника А. В. Лебедева

Оригинал-макет выполнен

в издательском объединении "ЮНИТИ"

О.В. Белынской, Н.В. Спасской

Лицензия № 071252 от 04.01.96

Подписано в печать 17.04.97. Формат 84х108 1/32

Усл. печ. л. 15,12. Тираж 5000 экз. Заказ 2304

Издательское объединение “ЮНИТИ”

Генеральный директор В.Н. Закаидзе

123298, Москва, Тепличный пер., 6

Тел. [phone]. Тел/факс [phone]

E-mail: [e-mail]

Отпечатано в ГУП ИПК “Ульяновский Дом печати”

432601, г. Ульяновск, ул. Гончарова, 14

[1] См.: Лаплас П. Опыт философии теории вероятностей. - М., 1908. -С.15.

[2] Вернадский В.И. Начало и вечность жизни. - М.: Республика, 1989. - С.156.

[3] Вернадский В.И. Биосфера и ноосфера. - М.: Наука, 1989. - С. 185.

[4] Вернадский В.И. Биосфера и ноосфера. - М.: Наука, 1989. - С. 181.

[5] Вернадский В.И. Биогеохимические очерки. - М., 1940. - С. 49.

[6] Вернадский В.И. Начало и вечность жизни. - М. - С. 184.

[7] Вернадский В.И. Научная мысль как планетное явление// Начало и вечность жизни. - С. 131.

[8] Вернадский В.И. Биосфера и ноосфера. С. 193.

[9] Одум Ю. Экология. - М.: Мир, 1986. - С. 13.

[10] Холл А.Д; Фейджин Р.Е. Определение понятия системы// Исследования по общей теории систем -М., 1966. - С.252.

В классической механике второй закон Ньютона для данного вида движе-

ния запишется в виде (2.1):

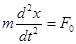, (2.1)

где F₀ - сила, действующая на частицу массы m.

Уравнение (2.1) элементарно интегрируется:

x(t)=x₀ + V₀t + 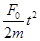(2.2)

Здесь x₀ и V₀ - начальные значения координаты и скорости.

Уравнение Шредингера для частицы, движущейся под действием посто-

янной силы имеет вид:

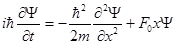
(2.3)

Начальная волновая функция, необходимая для решения нестационарного

уравнения Шредингера (2.3), задается волновым пакетом гауссовской фор-

мы:

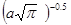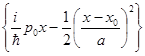Ψ(x, t=0) = ехр (2.4)

Поскольку уравнение (2.4) соответствует частице, движущейся в положи-тельном направлении оси х, случай F₀ <0 соответствует замедляющему

силовому полю, а случай F₀>0 – ускоряющему. Аналитическое решение

уравнения (2.3) для частицы, движущейся под действием постоянной силы

выполнено в [3] методом быстрого преобразования Фурье. Волновая функ-

ция при этом описывается довольно громоздким уравнением, что затрудня-

ет его анализ. Можно указать следующие особенности полученного реше-

ния:

1. “В среднем” под действием постоянной силы квантовая частица дви-жется так же, как и классическая частица:

,

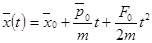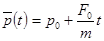, (2.5)

где 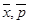- средние значения координаты и импульса, 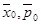- средние

значения этих величин в начальном состоянии.

2. Расплывание волнового пакета происходит с такой же скоростью, как

и в отсутствии внешнего поля. Характерное время расплывания можно

оценить по формуле (1.9) лабораторной задачи QM-1:

τ = ,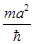

где a – начальная ширина пакета.

3. Характерный вид распределения плотности вероятности обнаружения

частицы при движении частицы в тормозящем поле в разные моменты

времени приведен на рис. 2.1. Тормозящая сила, как видно из рисунка,

естественно направлена в сторону, противоположную движению частицы.

Дата добавления: 2015-05-08