Приближенные вычисления в схеме Бернулли. Локальная и интегральная теоремы Лапласа

Задача 4. Вероятность выигрыша в лотерею на один билет равна р. Куплено n билетов. Найти: а) наивероятнейшее число выигравших билетов; б) соответствующую вероятность.

Решение (для нулевого варианта: p=0,3; n=13).Наивероятнейшее число выигравших билетов k ₀ определяется из двойного неравенства np–q ≤ k₀ < np+p, где (q=1–p). Авероятность того, что из 13 купленных билетов выигравших билетов окажется ровно k₀ находитсяпо локальной теореме Лапласа (т.к. n ≥ 10): , где x= 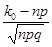. Подставив значения n и p, заданные для своего варианта, получим:

а). np–q ≤ k₀ < np+p, => 3,9-0,7 ≤ k₀ < 3,9+0,3 => k₀ = 4.

б). 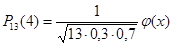, где φ(х)= , х= = .

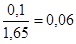Значения функции φ(х) для вычисленного значения х находятся по специальным справочным таблицам, которые имеются во всех учебниках, пособиях и справочниках по теории вероятности. Для х=0,06 находим φ(х)=0,3982. А искомая вероятность =0,24

Ответ: k₀ = 4, Р₁₃(4)=0,24.

Задача 5. Вероятность наступления некоторого события в каждом из n независимых испытаний равна р. Определить вероятность того, что число m наступлений события удовлетворяет следующему неравенству:

Варианты 0-11- k₁≤m≤ k₂; варианты 12-21- m≤ k₁; варианты 22-31- m≥k₂.

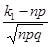Решение (для нулевого варианта: n=400, p=0,8, k₁=300. k₂=350). Вероятность того, что число появлений события А в n независимых испытаниях попадет в некоторый интервал [ k₁,k₂ ] определяется интегральной теоремой Лапласа: Р_n(k₁,k₂)= 1/2(Φ(X") –Φ(X')), где Φ(X)= - функция Лапласа, X'= , X"= . Значения функции Лапласа для вычисленных значений X' и X" находятся по специальным справочным таблицам, которые имеются во всех учебниках, пособиях и справочниках по теории вероятности. Следует учесть, что Φ(X)— нечетная функция, т.е. Φ(-X)= - Φ(X).

X'= 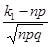= ; Φ(-2,5)= -0,9876; X"= = 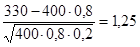; Φ(1,25)= 0,7887

Р_n(k₁,k₂)= 1/2(Φ(X") – Φ(X'))= 0,7887-(-0,9876)= 0,8882

Ответ: Р₄₀₀(300,330)=0,8882.

Контрольные вопросы.

1. Основные формулы комбинаторики.

2. Виды случайных событий.

3. Классическое определение вероятности.

4. Вероятности суммы и произведения событий.

5. Формула полной вероятности.

6. Формула Байеса.

7. Формула Бернулли.

8. Локальная и интегральная теоремы Лапласа.

Дата добавления: 2015-05-08