Постановка задачи

Компрессорная станция закачивает природный газ в подземное хранилище газа (ПХГ). Объёмная производительность компрессоров равна V_П. За время работы компрессорной станции избыточное давление в ПХГ повышается от начального Р_1изб до конечного Р_2изб, а температура изменяется от t₁ до t₂. Объём подземного хранилища равен V. Давление окружающего воздуха Р_о.с.=0.1МПа.

Исходные данные:

Природный газ (месторождение)	Р1изб, МПа	t1, ^0С	Р2изб, МПа	t2, ^0С	VП∙10^5, нм^3/ч	V∙10^6, м^3
Уренгойское (газоконденсатное)	3,3		8,5			0,9

Состав природного газа:

метан CH₄ – 98,23%

этан C₂H₆ – 0,1383%

бутан C₄H₁₀ – 0,0017%

азот N₂ – 1,24%

углекислый газ CO₂ – 0,39%

Определить. Массу газа G, закаченного в ПХГ и время закачки .

Решение:

1. Природный газ подчиняется закону Клапейрона.

Для G кг уравнение состояния идеального газа имеет вид:

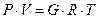
Массу газа, закаченного в газохранилище можно определить по соотношению:

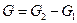
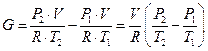
Характеристическая газовая постоянная смеси R зависит от кажущейся молекулярной массы смеси: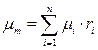

Молекулярные массы компонентов:

, ,

, , ,

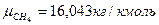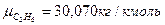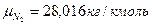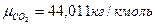Молекулярная масса смеси:

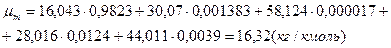
Характеристическая газовая постоянная смеси:

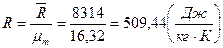
Учитывая, что абсолютные давления равны 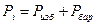, абсолютные температуры 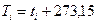, получаем:

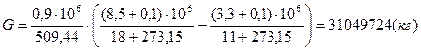
Рассчитаем плотность газа пр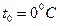и и 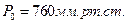, так как объемная производительность компрессорной станции задана при нормальных условиях:

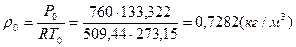
Время закачки газа определяем как отношение массы газа к массовой производительности компрессорной станции:

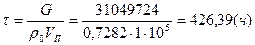
2. Природный газ не подчиняется уравнению Клапейрона, то есть газ реальный.

2.1 Расчёт с использованием уравнения состояния 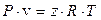, где z – это коэффициент сжимаемости газа. Масса закаченного в газохранилище газа определяется по соотношению: .

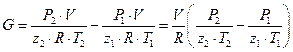а) Проведем расчёт по СТО Газпром :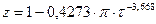

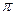и - это приведённые значения давления и температуры.

; ;

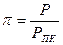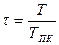Для смеси газов величины псевдокритического давления 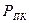и псевдокритической температуры 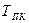определяем по соотношениям:

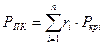
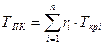, где 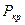, 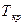- критические давления и температура компонентов газовой смеси.

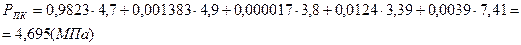
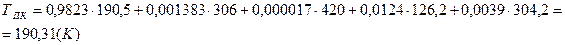
Определим приведённые значения давлений и температур:

; ;

; ;

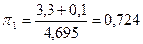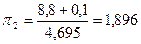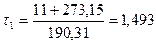Определяем значения коэффициентов сжимаемости:

; ;

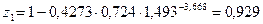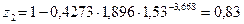Масса закаченного в газохранилище газа:

;

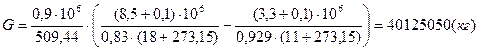Плотность природного газа при нормальных условиях: .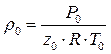

Приведённые давления и температура природного газа при нормальных условиях:

; ;

;

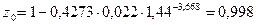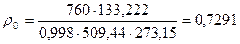(кг/м³);

Время закачки газа:

;

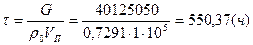б) Проведем расчёт по отраслевым нормам

1. ;

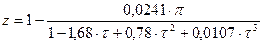Определяем значения коэффициентов сжимаемости:

;

;

;

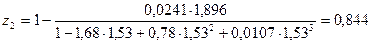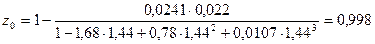Масса закаченного в газохранилище газа:

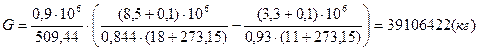
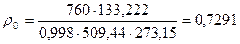(кг/м³);

Время закачки газа:

;

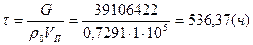2. ; ; .

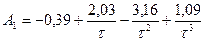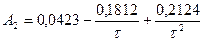Определяем значения коэффициентов сжимаемости:

;

;

;

;

;

;

;

;

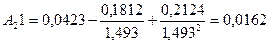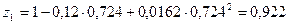
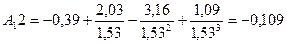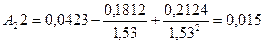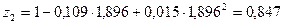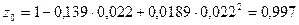Масса закаченного в газохранилище газа:

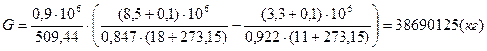
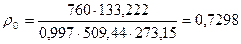(кг/м³);

Время закачки газа:

;

2.2 Расчёт по уравнению Редлиха-Квонга:

;

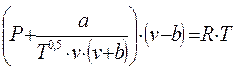Определим значения коэффициентов a и b:

;

;

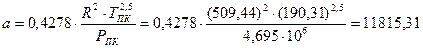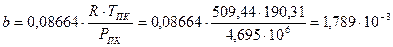Для определения массы закаченного в газохранилище газа необходимо из уравнения Редлиха-Квонга найти удельный объём, для этого воспользуемся методом простой итерации: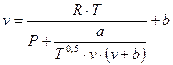

Определим :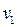

(*)

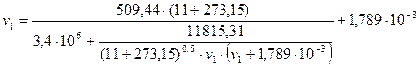Первоначальное значение 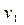можно определить по уравнению Клапейрона и подставить в правую часть соотношения (*). Затем полученное значение вновь подставить в правую часть соотношения (*) и так до достижения требуемой точности.

По уравнению Клапейрона определяем начальное значение:

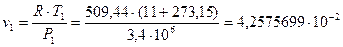(м³/кг);

В результате итерационного расчёта получим последовательность:

…

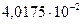
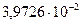
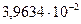
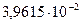
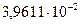
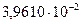С достаточной для расчёта точностью можно принять 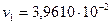(м³/кг)

Аналогично находим :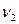

;

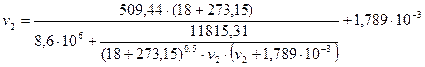В качестве первого значения берем

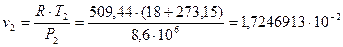
В результате итерационного расчёта получим последовательность:

…

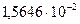
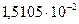
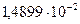
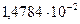
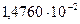С достаточной для расчёта точностью можно принять 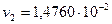(м³/кг)

Найдём массу газа, закачиваемого в газохранилище:

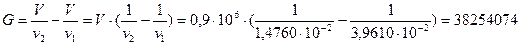(кг).

По уравнению Редлиха-Квонга найдём значение удельного объёма газа при нормальных условиях:

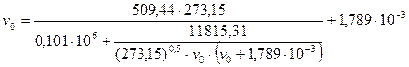
В качестве первого приближения выбираем

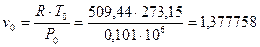(м³/кг)

В итоге по методу простой итерации получим:

1,377758; 1,374435; 1,374410…

В итоге 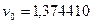(м³/кг).

Время закачки газа:

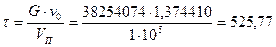(ч).

Оценим коэффициенты сжимаемости газа в условиях начала и конца закачки:

;

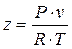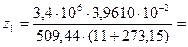0,930;

0,856;

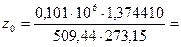0,998;

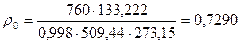
Результаты вычислений:

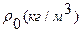
№ п/п	Параметры Уравнение				G (кг)	(ч)
	Клапейрона			0,7282		426,39
	СТО Газпром	0,929	0,830	0,7291		550,37
	Отраслевые нормы 1	0,930	0,844	0,7291		536,37
	Отраслевые нормы 2	0,922	0,847	0,7298		530,15
	Редлиха-Квонга	0,930	0,856	0,7290		525,77

Выводы:

Дата добавления: 2015-05-09