Математическая модель одноканальной СМО с отказами

Рассмотрим одноканальную систему массового обслуживания с ожиданием, в которую поступает поток пакетов с интенсивностью 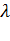; интенсивность обработки 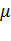, т. е. в среднем непрерывно занятый канал будет выдавать 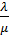обработанных пакетов в единицу (времени). Пакет, поступивший в момент, когда канал занят, становится в очередь и ожидает обработки.

Предположим сначала, что количество мест в очереди ограничено числом m, т. е. если пакет пришел в момент, когда в очереди уже стоит m пакетов, он покидает систему не обработанным. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.

Будем нумеровать состояния СМО по числу пакетов, находящихся в системе (как обрабатываемых, так и ожидающих обработки):

— канал свободен;

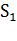— канал занят, очереди нет;

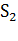— канал занят, один пакет стоит в очереди;

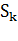— канал занят, k - 1 пакетов стоит в очереди;

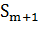— канал занят, t пакетов стоит в очереди.

Схема одноканальной СМО с ожиданием показана на рис. 1. Все интенсивности потоков событий, переводящих в систему по стрелкам слева направо, равны 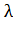, а справа налево — 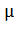. Действительно, по стрелкам слева направо систему переводит поток пакетов (как только придет пакет, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, имеющий интенсивность 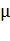(как только будет обработан очередной пакет, канал либо освободится, либо уменьшится число пакетов в очереди).

Рисунок. 1 Одноканальная СМО с ожиданием.

Изображенная на рис. 1 схема, представляет собой схему размножения и гибели. Напишем выражения для предельных вероятностей состояний:

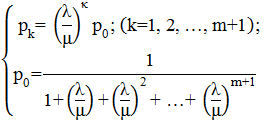
(1)

или с использованием :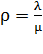

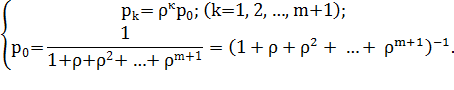
(2)

Последняя строка в (2) содержит геометрическую прогрессию с первым членом 1 и знаменателем 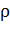; откуда получаем:

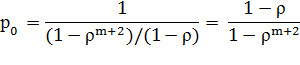
(3)

в связи с чем, предельные вероятности принимают вид:

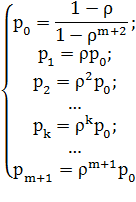
(4)

Выражение (3) справедливо только при 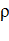< 1 (при 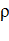= 1 она дает неопределенность вида 0/0). Сумма геометрической прогрессии со знаменателем 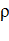= 1 равна m + 2, и в этом случае

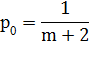
Определим характеристики СМО: вероятность отказа 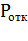, относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди 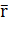, среднее число заявок, связанных с системой 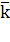, среднее время ожидания в очереди 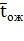, среднее время пребывания заявки в СМО .

Вероятность отказа. Очевидно, пакет получает отказ только в случае, когда канал занят и все т мест в очереди тоже:

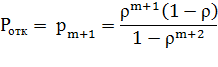
(5)

Относительная пропускная способность:

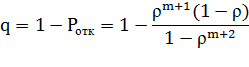
(6)

Абсолютная пропускная способность:

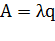
Средняя длина очереди. Найдем среднее число 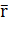пакетов, находящихся в очереди, как математическое ожидание дискретной случайной величины R — числа пакетов, находящихся в очереди:

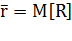
С вероятностью 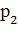в очереди стоит один пакет, с вероятностью 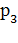— два пакета, с вероятностью 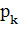в очереди стоит k - 1 пакетов, и т. д., откуда:

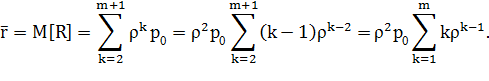
(7)

Поскольку 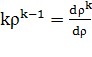, сумму в (7) можно трактовать как производную по 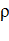от суммы геометрической прогрессии:

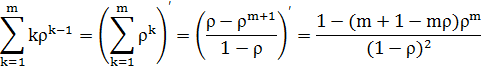
Подставляя данное выражение в (7) и используя 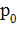из (4), окончательно получаем:

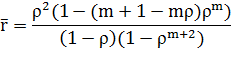
(8)

Среднее число пакетов, находящихся в системе. Получим далее формулу для среднего числа 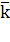пакетов, связанных с системой (как стоящих в очереди, так и находящихся на обработке). Поскольку 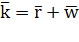, где 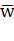— среднее число пакетов, находящихся под обслуживанием, а k известно, то остается определить 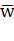. Поскольку канал один, число обслуживаемых пакетов может равняться 0 (с вероятностью 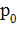) или 1 (с вероятностью 1 - 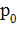), откуда:

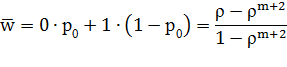
и среднее число пакетов, связанных с СМО, равно

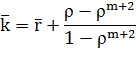
(9)

Среднее время ожидания пакета в очереди. Обозначим его 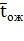; если пакет приходит в систему в какой-то момент времени, то с вероятностью 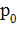канал не будет занят, и ему не придется стоять в очереди (время ожидания равно нулю). С вероятностью 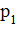он придет в систему во время обслуживания какого-то пакета, но перед ним не будет очереди, и пакет будет ждать начала своей обработки в течение времени 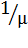(среднее время обработки одного пакета). С вероятностью 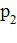в очереди перед обрабатываемым пакетом будет стоять еще один, и время ожидания в среднем будет равно 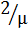, и т. д.

Если же k = m + 1, т. е. когда вновь приходящий пакет застает канал обслуживания занятым и m пакетов в очереди (вероятность этого 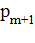), то в этом случае пакет не становится в очередь (и не обрабатывается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:

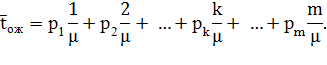
Если подставить сюда выражения для вероятностей (4.4), получим:

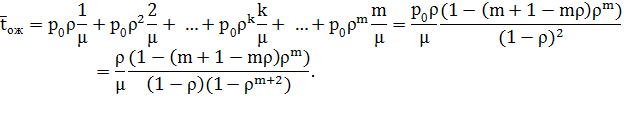
(10)

Здесь использованы соотношения (7), (8) (производная геометрической прогрессии), а также 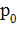из (4). Сравнивая это выражение с (8), замечаем, что иначе говоря, среднее время ожидания равно среднему числу пакетов в очереди, деленному на интенсивность потока поступления пакетов.

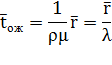
(11)

Среднее время пребывания пакета в системе. Обозначим математическое ожидание случайной величины — время пребывания пакета в СМО, которое складывается из среднего времени ожидания в очереди 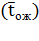и среднего времени обслуживания 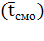. Если загрузка системы составляет 100 %, очевидно, 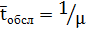, в противном же случае 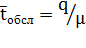. Отсюда:

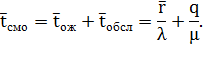
Дата добавления: 2015-05-09