
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Человеко-машинная процедура STEM
|
|
|
|
Одной из первых ЧМП была разработана процедура STEM [28, 35]. Она предназначена для решения многокритериальных задач линейного программирования.
Пусть  — вектор переменных задач;
— вектор переменных задач;
 , i =
, i = 
 (5.1)
(5.1)
— целевая функция по критерию i, определяемая на множестве переменных X и векторе C, значение которой необходимо максимизировать.
Пусть множество допустимых значений X ограничено системой  :
:
 , (5.2)
, (5.2)
X  0,
0,
где A — матрица 
B — вектор-столбец размерностью  .
.
Пусть  — общая функция предпочтений (функция полезности) на множестве целевых функций
— общая функция предпочтений (функция полезности) на множестве целевых функций  определяется в виде взвешенной суммы критериев.
определяется в виде взвешенной суммы критериев.

Необходимо найти вектор (аргумент) X, максимизирующий совокупность целевых функций  при наиболее предпочтительном соотношении их значений в точке решения X и удовлетворяющей системе ограничений (6.2), то есть необходимо найти решение
при наиболее предпочтительном соотношении их значений в точке решения X и удовлетворяющей системе ограничений (6.2), то есть необходимо найти решение
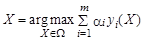 .
.
Решение этой задачи — вектор X следует искать во множестве Парето-эффективных решений, а требование нахождения наиболее предпочтительного (неявно выраженного) соотношения между значениями критериев со стороны лица, принимающего решение, в человеко-машинных процедурах выражается, как правило, в большинстве своем в поиске весовых коэффициентов 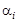 целевых функций.
целевых функций.
Поскольку назначение весовых коэффициентов является для ЛПР сложной операцией, то в человеко-машинной процедуре STEM определение 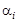 поручается ЭВМ.
поручается ЭВМ.
Задача многокритериальной оптимизации представляется как задача поиска удовлетворительного (компромиссного) решения, формализуемого в виде условий
 i = 1, 2,…, m, (5.3)
i = 1, 2,…, m, (5.3)
где 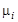 — пороговые значения критериев, выделяющие множество удовлетворенных решений и назначаемые ЛПР.
— пороговые значения критериев, выделяющие множество удовлетворенных решений и назначаемые ЛПР.
Так как удовлетворительное значение порога  в общем случае зависит от значений других критериев
в общем случае зависит от значений других критериев  то условия (6.3) корректируются в ходе человеко-машинной процедуры по мере анализа новых альтернатив и изменения предпочтений ЛПР о множестве допустимых решений.
то условия (6.3) корректируются в ходе человеко-машинной процедуры по мере анализа новых альтернатив и изменения предпочтений ЛПР о множестве допустимых решений.
Человеко-машинная процедура STEM состоит из следующих фаз: оптимизации —  (выполняются на ЭВМ) и анализа —
(выполняются на ЭВМ) и анализа — 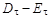 (выполняются ЛПР,
(выполняются ЛПР,  — номер итерации):
— номер итерации):
Шаг 
1. Вычисляется матрица  , где
, где  — значение целевой функции по критерию
— значение целевой функции по критерию  , найденное на решении
, найденное на решении  , то есть
, то есть 
Решение  определяется в результате решения локальной задачи оптимизации целевой функции по k -му критерию
определяется в результате решения локальной задачи оптимизации целевой функции по k -му критерию  в текущей области допустимых решений
в текущей области допустимых решений  , то есть
, то есть
 .
.
 на первой итерации определяется системой уравнений (4.2). На последующих итерациях к ней будет добавляться по одному ограничению вида (6.3), накладываемого на наиболее не удовлетворяющий критерий.
на первой итерации определяется системой уравнений (4.2). На последующих итерациях к ней будет добавляться по одному ограничению вида (6.3), накладываемого на наиболее не удовлетворяющий критерий.
2. Нормируется матрица 

где  ;
; 
Очевидно, что для диагональных элементов 
3. Рассчитывается система весовых коэффициентов 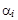 критериев i:
критериев i:
 ; i = 2, …, N;
; i = 2, …, N;  ;
;
где 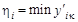 или,
или,  ,
,
где  — среднее значение элементов I-ой строки (исключая максимальный).
— среднее значение элементов I-ой строки (исключая максимальный).
Шаг 
1. Определяется вектор компромиссного решения  на итерации
на итерации  , максимизирующий функцию полезности
, максимизирующий функцию полезности
 .
.
2.Вычисляется вектор критериальных оценок  , соответствующий компромиссному решению
, соответствующий компромиссному решению  .
.
Шаг 
Формируется сообщение ЭВМ на итерации 
 ,
,
где  — вектор критериальных оценок, соответствующий идеальным решениям
— вектор критериальных оценок, соответствующий идеальным решениям 
Шаг 
Оценивается предлагаемое решение на основании сопоставления векторов  и
и 
Если ЛПР считает это решение удовлетворительным, завершается процедура, иначе переход к шагу  .
.
Шаг 
ЛПР указывает, какой из критериев в векторе  имеет наименее удовлетворительное значение, и устанавливает желаемую величину порога удовлетворенности
имеет наименее удовлетворительное значение, и устанавливает желаемую величину порога удовлетворенности  (i — номер неудовлетворяющего критерия). Таким образом, информация ЛПР имеет вид:
(i — номер неудовлетворяющего критерия). Таким образом, информация ЛПР имеет вид:
 .
.
Перейти к шагу  (размерность матрицы
(размерность матрицы  уменьшится на единицу, так как критерий i «уйдет» в область ограничений).
уменьшится на единицу, так как критерий i «уйдет» в область ограничений).
Пример
Обратимся к задаче определения плана выпуска продукции, рассмотренной в разделе 2.1. Добавим еще один критерий определения плана: минимизация суммарного времени простоя оборудования (максимизация загрузки оборудования). В целом, необходимо определить план производства столов и шкафов с учетом трех критериев:
1) максимизация дохода от реализации продукции (в рублях)

где  — план выпуска столов, предназначенных для продажи,
— план выпуска столов, предназначенных для продажи,
 — план выпуска шкафов, предназначенных только для продажи;
— план выпуска шкафов, предназначенных только для продажи;
2) максимизация выпуска столов для нужд всего предприятия (в штуках)
 ,
,
где  — план выпуска столов, предназначенных для собственных нужд предприятия;
— план выпуска столов, предназначенных для собственных нужд предприятия;
3) максимизация загрузки оборудования (в часах)
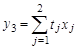 ,
,
где 
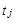 — время изготовления одного продукта j -ого вида (час).
— время изготовления одного продукта j -ого вида (час).
Пусть время изготовления одного стола 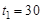 минут, время изготовления одного шкафа
минут, время изготовления одного шкафа 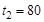 минут.
минут.
Решением задачи определения плана выпуска продукции с учетом только первого критерия является вектор 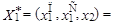 (517; 0; 156), то есть столов на продажу следует производить в количестве
(517; 0; 156), то есть столов на продажу следует производить в количестве  штук, столов для собственных нужд — не производить
штук, столов для собственных нужд — не производить  = 0, шкафов — производить в количестве
= 0, шкафов — производить в количестве 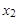 = 156 штук. Значение первого критерия
= 156 штук. Значение первого критерия  = 375500 рублей.
= 375500 рублей.
Решением задачи с учетом только второго критерия является вектор  = (0;700;0), то есть столов (для собственных нужд предприятия) следует производить в количестве
= (0;700;0), то есть столов (для собственных нужд предприятия) следует производить в количестве  = 700 штук. Значение второго критерия
= 700 штук. Значение второго критерия  = 700 штук.
= 700 штук.
Решением задачи с учетом только третьего критерия является множество решений  , то есть столов в общей сумме следует производить
, то есть столов в общей сумме следует производить  = 279 штук (0
= 279 штук (0  ), а шкафов — в количестве
), а шкафов — в количестве 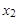 = 268 штук. Значением третьего критерия является величина
= 268 штук. Значением третьего критерия является величина
 +
+  = 497 часов.
= 497 часов.
Процедура STEM включает следующие шаги.
Шаг 
1. Рассчитывается матрица 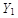 (табл. 5.1)
(табл. 5.1)
 =
=  рублей;
рублей;

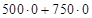 = 0 рублей;
= 0 рублей;

 рублей.
рублей.
При  то есть если все столы пустить на продажу,
то есть если все столы пустить на продажу,  = 340500 рублей. При
= 340500 рублей. При  = 0, то есть если все столы оставить для нужд предприятия,
= 0, то есть если все столы оставить для нужд предприятия,  = 201000 рублей. Таким образом, 340500
= 201000 рублей. Таким образом, 340500 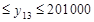 .
.
 штук,
штук,
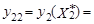 700 штук,
700 штук,
 штук.
штук.
То есть  изменяется от 0 до 279 штук
изменяется от 0 до 279 штук  .
.

 = 466.5 час.
= 466.5 час.

 час.
час.
 497час.
497час.
Таблица 5.1 — Значение критериев при различных оптимальных решениях
| Критерии | Решения 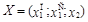
| ||
 (517;
0;156) (517;
0;156)
|  (0;700;0) (0;700;0)
|  ( ( 279;
(1– 279;
(1–  )279; 268) )279; 268)
| |
 (тыс.руб.) (тыс.руб.)
| 375.5 | 201  340.5 340.5
| |
 (шт.) (шт.)
| 0  279 279
| ||
 (час) (час)
| 466.5 |
2. Нормируем матрицу 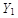 по каждому из критериев, приняв
по каждому из критериев, приняв  = (201+340.5)/2 = 270.75 рублей и
= (201+340.5)/2 = 270.75 рублей и  139 штук.
139 штук.

| 0.72 | 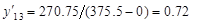

 =
= 116.5:147 = 0.79 =
= 116.5:147 = 0.79
| ||
| 0.2 | ||||
| 0.79 |
3. Рассчитываются весовые коэффициенты 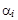 .
.
 ;
; 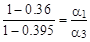 ;
; 
 0.9
0.9  – 0.64
– 0.64  = 0;
= 0;
0.605  – 0.64
– 0.64  = 0;
= 0;
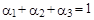 .
.
Решая эту систему уравнений, получаем:
 = 0.3;
= 0.3;  = 0.42;
= 0.42;  = 0.28.
= 0.28.
Шаг 
1. Определяется решение по глобальному критерию 

Решая задачу линейного программирования
0.3  +0.42
+0.42  +0.28
+0.28  max
max
при ограничениях на ресурсные параметры:
0.06  0.06
0.06  0.07
0.07  42
42
0.04  0.04
0.04  +0.085
+0.085  34 (
34 ( )
)
0.035  +0.035
+0.035  +0.12
+0.12  42
42
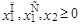 ,
,
 — целые.
— целые.
Получим компромиссное решение  с координатами
с координатами
 = 0;
= 0;  = 517;
= 517; 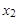 = 156.
= 156.
2. Вектор критериальных оценок  для решения
для решения 
 = {117 тыс. руб.; 517 шт.; 466.5 час}.
= {117 тыс. руб.; 517 шт.; 466.5 час}.
Шаг 
Формируется сообщение ЭВМ для ЛПР  :
:
| Вектор оценок | Критерии | ||

| 
| 
| |
Вектор  идеальных
решений идеальных
решений 
| 375.5 тыс. руб. | 700 шт. | 497 час |
Вектор  компромиссных решений компромиссных решений
| 117 тыс. руб. | 517 шт. | 466.5 час |
Шаг 
ЛПР оценивает компромиссное решение по значениям критериев. Если он считает это решение удовлетворительным, то процедура поиска на этом заканчивается. Иначе переходим на следующий шаг.
Шаг 
ЛПР указывает, какой из критериев в векторе  имеет наименее удовлетворительное значение. Пусть он указывает на критерий 1 и устанавливает порог в 300 тыс. руб., то есть дает сообщение
имеет наименее удовлетворительное значение. Пусть он указывает на критерий 1 и устанавливает порог в 300 тыс. руб., то есть дает сообщение
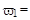 {1; 300 тыс. руб.}.
{1; 300 тыс. руб.}.
Переходим на шаг  .
.
Шаг 
1. Рассчитывается матрица 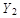
| Критерии | Решения 
| |
 (0;700;0) (0;700;0)
|  ( ( 279;(1 – 279;(1 –  )279;268) )279;268)
| |
 (шт.) (шт.)
| 0  279 279
| |
 (час) (час)
|
2. Нормируем таблицу 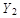 по каждому из критериев, приняв
по каждому из критериев, приняв  = 139 шт.
= 139 шт.

| ||
3. Рассчитываются весовые коэффициенты  и
и  :
:
 = 0.5;
= 0.5;  = 0.5.
= 0.5.
Шаг 
1. Определяется решение по глобальному критерию
 .
.
Решаем задачу
0.5  +0.5
+0.5  max
max
при ограничениях на ресурсные параметры ( ) и на значение критериальной функции
) и на значение критериальной функции 
500  +750
+750 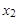
 300000.
300000.
Получим новое компромиссное решение  с координатами
с координатами  = 365;
= 365;  = 152;
= 152; 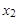 = 156.
= 156.
2. Вектор критериальных оценок  для решения
для решения 
 = {300 тыс. руб.; 152 шт.; 466.5 час.}.
= {300 тыс. руб.; 152 шт.; 466.5 час.}.
Шаг  . Формируется сообщение для ЛПР
. Формируется сообщение для ЛПР 
| Вектор оценок | Критерии | ||

| 
| 
| |
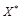 идеальных решений идеальных решений
| 375.5 тыс. руб. | 700 шт. | 497 час |
 компромиссных
решений компромиссных
решений
| 300 тыс. руб. | 152 шт. | 466.5 час |
Шаг 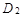
ЛПР оценивает полученное решение. Если оно считает это решение удовлетворительным, то процедура поиска решения заканчивается, иначе повторяются шаги  .
.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 1467; Нарушение авторских прав?; Мы поможем в написании вашей работы!