Метод узловых напряжений

Метод узловых напряжений заключается в определении на основании первого закона Кирхгофа потенциалов в узлах электрической цепи относительного некоторого базисного узла. Базисный узел в общем случае выбирается произвольно, потенциал этого узла принимается равным нулю. Разности потенциалов рассматриваемого и базисного узлов называется узловым напряжением.

На рис.29 представлена схема электрической цепи, содержащая пять ветвей и три узла. За базисный принят узел с индексом «0».

Узловое напряжение U₁₀=j₁-j₀. Положительное напряжение узловых напряжений указывается стрелкой от рассматриваемого узла к базисному.

Рис.29. Иллюстрация к методу узловых напряжений.

Напряжение на ветвях цепи равно, очевидно, разности узловых напряжений концов данной ветви. Например, напряжение ветви 4 равно: U₄=I₄R₄=U₁₀-U₂₀ (30)

Из формулы (30) видно, что, зная узловые напряжения, можно найти ток ветви.

Структуру уравнений получим, рассматривая схему рис.30.

Т.к. узел с индексом «0» принят за базисный, то его потенциал равен нулю. Узловые напряжения (потенциалы) узлов 1 и 2 – неизвестны.

Уравнения по первому закону Кирхгофа для 1 и 2 узлов соответственно записываются:

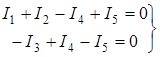(31)

Узловое напряжение 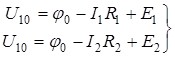(32)

Отсюда 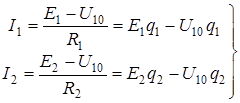(33,а)

Аналогично для оставшихся токов:

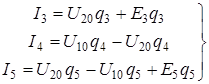(33,б)

Выражения (33,а,б) подставляем в систему (31) и после некоторых арифметических преобразований получаем:

(34)

Обозначим q₁₁=q₁+q₂+q₄+q₅ – собственная проводимость узла 1.

q₂₂=q₃+q₄+q₅ – собственная проводимость узла 2.

q₁₂=q₂₁=q₄+q₅ – взаимная проводимость ветви, соединяющей узлы 1 и 2.

I_y1=E₁q₁+E₂q₂+E₅q₅ – узловой ток узла 1.

I_y2=-E₃q₃-E₅q₅ – узловой ток узла 2.

Из приведенных выражений видно:

Собственная проводимость узла равна сумме проводимостей ветвей, сходящихся в данном узле.

Взаимная проводимость равна сумме проводимостей ветвей, соединяющих данные узлы.

Узловой ток (теоретическое понятие) – это алгебраическая сумма произведений E_iq_i и J_i источников тока (если они есть) всех ветвей, примыкающих к рассматриваемому узлу. Слагаемое входит в выражение со знаком «+», если э.д.с. и источник тока направлены к узлу. В противном случае – ставится знак «-».

После введенных обозначений система (34) принимает вид:

(35)

Из формул (35) видно, что собственная проводимость входит в выражения со знаком «+», а взаимная проводимость – со знаком «-».

Для произвольной схемы, содержащей n+1 узлов, система уравнений по методу узловых напряжений имеет вид:

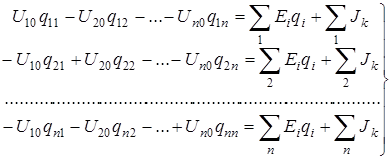(36)

Число уравнений, составляемое по методу узловых напряжений, равно

N_ур=N_y-1-N_э.д.с. (37)

где N_э.д.с. – число идеальных источников э.д.с.

Пример: (общий случай)

Пример: (с идеальными э.д.с.)

Порядок расчета электрических цепей по методу узловых напряжений:

1. Выбираем произвольно базисный узел. Желательно нулевой потенциал представить тому узлу, где сходится большее количество ветвей. Если имеется ветвь, содержащая идеальную э.д.с., то базисный узел должен быть концом или началом этой ветви.

2. Составляется система уравнений для неизвестных узловых напряжений в соответствии с общей структурой этих уравнений (36).

3. Решая данную систему, находят напряжения узлов относительно базиса.

4. Токи ветвей определяют по обобщенному закону Ома:

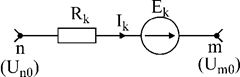
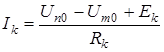(38)

Следствие: Если схема содержит только два узла, то в соответствие с методом узловых напряжений (в отсутствие идеальных э.д.с.) составляется только одно уравнение.

Например, для схемы рис.30:

U₁₀q₁₁=E₁q₁-E₃q₄+J₂ (39)

Формула (39) носит название метода двух узлов.

Рис.30. Иллюстрация к методу двух узлов.

Узловое напряжение по методу двух узлов равно:

(40)

Пример: Дано: E₁=8B; E₅=12B; R₁=R₃=1 Ом; R₂=R₄=2 Ом; R₅=3 Ом.

Определить все токи методом узловых напряжений.

Рис.1

Решение:

Т.к. электрическая цепь содержит три узла и не содержит ветвей с идеальными источниками э.д.с., то число уравнений, составляемых по методу узловых напряжений равно 2.

Узел 3 будем считать базисным.

Тогда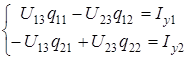

Где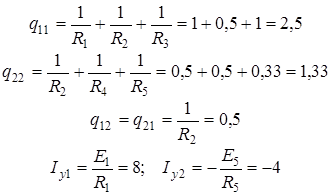

В результате решения системы определяем U₁₃=2,8 B; U₂₃=-1,95 B.

Токи в ветвях определяем по закону Ома:

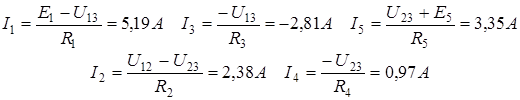
Метод наложения (суперпозиции).

Метод наложения основан на применении принципа наложения, который формулируется следующим образом:

Ток в любой ветви электрической цепи равен сумме токов, обусловленных действием каждого источника в отдельности, при отсутствии других источников.

Рассматриваемый принцип называют принципом независимого действия.

При действии только одного из источников напряжения предполагается, что э.д.с. всех остальных источников равны нулю, так же как равны нулю и токи всех источников тока. Отсутствие напряжения на зажимах источников напряжения равносильно короткому замыканию их зажимов. Отсутствие тока в ветви с источником тока равносильно разрыву этой ветви.

Если источник э.д.с. содержит внутреннее сопротивление, то, полагая э.д.с. равной нулю, следует оставлять в его ветви внутреннее сопротивление. Аналогично в случае источника тока с параллельной внутренней проводимостью, следует, разрывая ветвь источника (т.е. полагая J=0), оставлять включенной параллельную ветвь с внутренним сопротивлением.

Пусть в цепи действуют источники с параметрами E и J, I^//_n и I^/_n – токи n-ой ветви, создаваемые каждым из этих источников в отдельности. Искомый ток

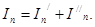
Принцип суперпозиции применим к напряжениям, т.к. между током и напряжением рассматривается линейная зависимость (закон Ома); но не применим к мощности:

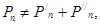
т.к. мощности – это квадратичные функции токов.

Пример.

Дано: E=60B; J=2A; R₁=5Ом; R₂=20Ом; R₃=10Ом; R₄=15Ом

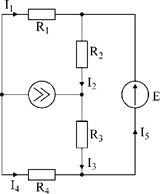
Рис.1

Определить все токи методом наложения.

Решение:

1. Заменяем источник э.д.с. E короткозамкнутым участком (т.к. его r_вн=0) (схема рис.2).

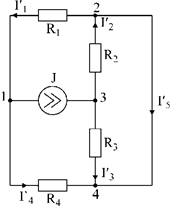
Рис.2

Т.к. конфигурация цепи изменилась, то в цепи рис.2 протекают токи отличные от токов цепи рис.1. Их называют первые частичные токи и обозначают со штрихом.

Т.к. схема упростилась, то токи можно рассчитать, применяя правило плеч. Схему цепи рис.2 более наглядно представим на рис.3.

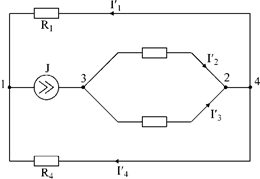
Рис.3

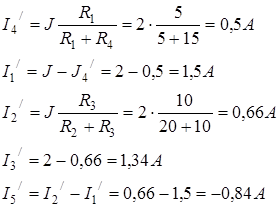
2. Разорвем ветвь с источником тока J. Токи, протекающие в цепи рис.4 называют вторыми частичными токами и обозначают с двумя штрихами.

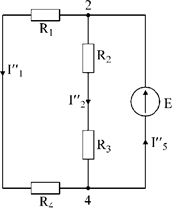
Рис.4

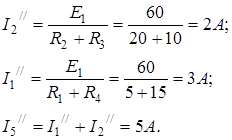
3. Искомые токи найдем как алгебраическую (т.е. с учетом направлений) сумму частичных токов:

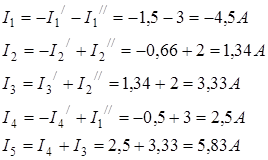
Дата добавления: 2015-05-09