Энергия и импульс

Сложение скоростей

Непосредственным следствием преобразований Лоренца является релятивистское правило сложения скоростей. Если некоторый объект имеет компоненты скорости 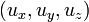относительно системы S и — относительно S', то между ними существует следующая связь:

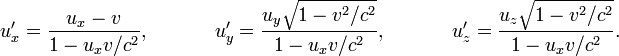
В этих соотношениях относительная скорость движения систем отсчёта v направлена вдоль оси x. Релятивистское сложение скоростей, как и преобразования Лоренца, при малых скоростях (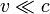) переходит в классический закон сложения скоростей.

Если объект движется со скоростью света 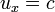вдоль оси x относительно системы S, то такая же скорость у него будет и относительно S': 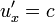. Это означает, что скорость является инвариантной (одинаковой) во всех ИСО.

Релятивистский и классический импульс, m=1

Если частица с массой m движется со скоростью , то её энергия и импульс имеют следующую зависимость от скорости:

Эти соотношения обобщают классические выражения для энергии и импульса, получающиеся в результате разложения в ряд по :

При нулевой скорости энергия частицы называется энергией покоя: 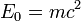. В современной физической литературе принято, что m — масса частицы не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. Понятие «релятивистской массы», зависящей от скорости не используется ^[25], хотя оно и встречается в ранних работах по теории относительности. Историческая причина введения этого понятия была связана с попытками сохранить для релятивистского импульса классическую форму: .

При приближении скорости тела к скорости света его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты не способны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях, близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4 относительная разница релятивистского и классического импульса составляет всего 3%.

Между релятивистской энергией и импульсом существуют следующие связи:

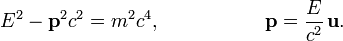
Эти формулы остаются справедливыми и для объектов, движущихся со скоростью света. В этом случае их масса должна быть равна нулю .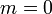

Масса движущихся релятивистских частиц зависит от их скорости:

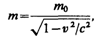(39.1)

где m ₀ — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в ваку­уме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона

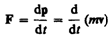
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.

Основной закон релятивистской динамики материальной точки имеет вид

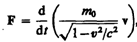(39.2)

или

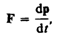(39.3)

где

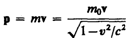(39.4)

— релятивистский импульс материальной точки.

Отметим, что уравнение (39.3) внешне совпадает с основным уравнением ньютоновской механики (6.7). Однако физический смысл его другой: справа стоит производ­ная по времени от релятивистского импульса, определяемого формулой (39.4). Таким образом, уравнение (39.2) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учиты­вать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.

В силу однородности пространства в релятивистской механике выполняет­ся закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выраже­ние для импульса.

Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости с, уравнение (39.2) переходит в основной закон (см. (6.5)) классичес­кой механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v<<c. Законы классической механики получаются как следствие теории относительности для предельного случая v<<c (формально пере­ход осуществляется при с ®¥). Таким образом, классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).

Экспериментальное доказательство зависимости массы от скорости (39.1) является подтверждением справедливости специальной теории относительности. В дальнейшем будет показано, что на основании этой зависимости производятся расчеты ускорителей.

Дата добавления: 2015-05-09