Сумматоры. Регистры сдвига или сдвиговые регистрыпредназначены для сдвига числа на одну позицию каждый раз, когда вводится новое число

Регистры сдвига

Регистры сдвига или сдвиговые регистры предназначены для сдвига числа на одну позицию каждый раз, когда вводится новое число.

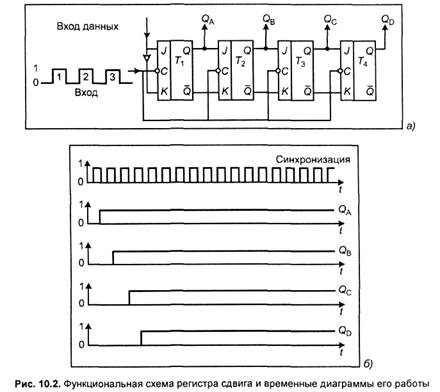
Регистры сдвига обладают временной памятью. Регистры сдвига реализуются на триггерах. На рис. 10.2 приведена схема режима сдвига, реализованного на Ж-триггерах.

За четыре полных такта логическая единица с входа первого разряда передается на выход Q последнего разряда. На рис. 10.2, б приведены временные диаграммы работы четырехразрядного регистра сдвига.

Предполагается, что первоначальное состояние регистра нулевое, а логическое состояние на входе является логической единицей и не изменяется в течение четырех тактов синхронизации.

Если данные вводятся поразрядно, то регистр называется последовательным регистром сдвига.

Существует и параллельная загрузка, при которой информационные разряды вводятся в регистр одновременно по команде одного тактового импульса.

Сумматор представляет собой логический операционный узел, выполняющий арифметическое сложение кодов двух чисел в цифровых устройствах.

При арифметическом сложении выполняются различные дополнительные операции: учет знаков чисел, выравнивание порядков слагаемых и т. д.

Сумматоры квалифицируют по различным признакам, например по числу входов и выходов.

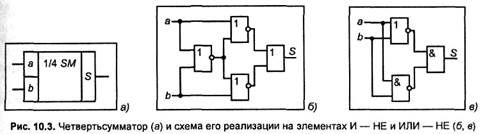
На рис. 10.3 показан четвертьсумматор с двумя входами для двух одноразрядных чисел и одним выходом, на котором реализуется их сумма.

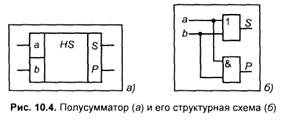
На рис. 10.4, а показан полусумматор с двумя входами, на которые подаются одноименные разряды двух чисел, и двумя выходами, на одном из которых реализуется арифмети­ческая сумма, а на другом — перенос в следующий более старший разряд. Обозначением полусумматора служат буквы HS (halfsum — полусумма).

Полусумматор может быть реализован на элементе исключающих ИЛИ и одном двухвходовом вентиле И (рис. 10.4, б).

Полные одноразрядные сумматоры характеризуются наличием трех входов, на которые подаются одномерные разряды двух складываемых чисел и перенос из предыдущего бо-

лее младшего разряда, и двумя выходами, на одном из которых реализуется арифметическая сумма в данном разряде, а на другом — перенос в более старший разряд.

Схема полного сумматора, реализованного на двух полусумматорах, показана на рис. 10.5, а.

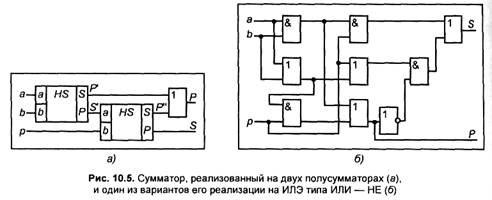
Сумматор на схемах обозначается SM. На входы а и b сумматора подаются два слагаемых, на вход р— перенос из предыдущего несущего разряда. Выходы обеспечивают суммирование по каналу S и перенос в старший разряд по каналу Р.

Особенностью выходных сигналов полного двоичного сумматора является их самодвойственность как функций алгебры логики. Другими словами, выходные сигналы S и Р способны инвертировать свое значение при инвертировании всех переменных, от которых они зависят.

Полные сумматоры совместно с инверторами используются для проведения операций вычитания. Сумматоры и вычитатели реализованы в виде интегральных схем.

Дата добавления: 2015-05-09