Создание цифровых фотопланов

Методы создания цифровых трансформированных изображений местности (объекта).

Назначение и области применения цифрового трансформирования снимков

Трансформированием снимков в фотограмметрии называют процесс преобразования исходного снимка объекта в изображение объекта в заданной проекции.

При цифровом трансформировании исходный снимок представляет собой цифровое изображение, получаемое или непосредственно цифровой съемочной системой или путем преобразования аналогового снимка в цифровую форму на сканере.

Основными областями применения цифрового трансформирования являются топография и картография.

При создании и обновлении карт различного назначения по аэрокосмическим снимкам создаются трансформированные изображения местности в проекции карты. Эти изображения могут быть созданы по одиночным снимкам или по нескольким перекрывающимся снимкам. Цифровое трансформирование выполняется с точностью, соответствующей точности предъявляемой действующими нормативными документами к точности карт соответствующего масштаба.

Цифровые трансформированные изображения используют для создания контурной части карт, путем векторизации цифровых изображений в среде CAD или ГИС, а также как самостоятельные картографические документы. В частном случае, если при трансформировании снимков не учитывается влияние кривизны Земли и проекции карты на положение контуров, трансформированное изображение представляет собой ортогональную проекцию местности на горизонтальную плоскость. Такой вид трансформирования называется ортофототрансформированием.

Помимо топографии и картографии, цифровое трансформирование используется для создания по исходным снимкам перспективных изображений местности из заданных точек пространства. Такие изображения используют в военной области, например, в летных тренажерах и в архитектуре - при проектировании различных сооружений.

Цифровое трансформирование применяют также для преобразования стереопар исходных снимков в стереопару снимков идеального случая съемки в системе координат фотограмметрической модели. Такое преобразование выполняется в цифровых стереофотограмметрических системах.

В настоящей главе рассматриваются теоретические основы цифрового фототрансформирования снимков, в частности, методы наблюдения и измерения цифровых снимков и методы создания цифровых трансформированных снимков и фотопланов.

Рассмотрим процесс цифрового трансформирования исходного снимка на примере его преобразования в цифровое трансформированное изображение, представляющее собой ортогональную проекцию местности на горизонтальную плоскость (ортофотоснимок).

Принципиальная схема этого процесса представлена на рис.1.1.

В результате цифрового трансформирования исходный снимок преобразуется в цифровое изображение местности, представляющее собой ортогональную проекцию местности на горизонтальную плоскость.

Принципиальная схема цифрового трансформирования снимков.

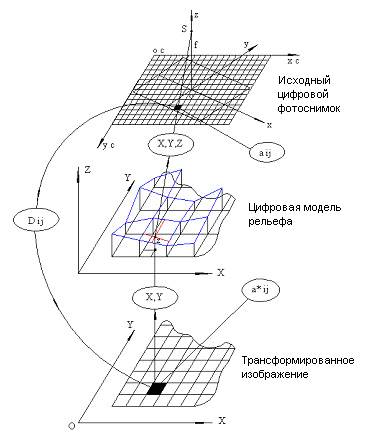
Рис.1.1

Исходными материалами при цифровом трансформировании снимков служат:

- цифровое изображение исходного фотоснимка;

- цифровая модель рельефа (ЦМР)

- значение элементов внутреннего и внешнего ориентирования снимков;

- значение параметров внутреннего ориентирования снимка в системе координат цифрового изображения.

В большинстве случаев при трансформировании снимков используется цифровая модель местности в виде матрицы высот, представляющей собой регулярную сетку квадратов на местности, стороны которых параллельны осям X и Y системы координат объекта 0XYZ. Координаты и высоты узлов сетки квадратов определены в системе координат объекта.

Для формирования ЦМР в виде матрицы высот, в большинстве случаев, используют цифровые модели рельефа, созданные в результате стереофотограмметрической обработки снимков или по уже существующим топографическим картам.

Наиболее распространённым методом построения цифровых моделей рельефа местности является, в настоящее время, метод триангуляции Делоне, в котором рельеф местности представлен в виде пространственной сети треугольников, координаты и высоты вершин которых определены в системе координат объекта. Рельеф местности в пределах треугольника в этом виде ЦМР, аппроксимируется плоскостью, проведённой через его вершины.

При формировании ЦМР этим методом по высотным пикетам треугольники генерируются под условием, чтобы в окружность, проведенную через вершины треугольников, не должны попадать вершины других треугольников.

По цифровой модели рельефа в виде триангуляции Делоне можно сформировать ЦМР в виде матрицы высот.

рис.1.2

Для определения высоты узла i матрицы высот, по координатам x_i и y_i этого узла в системе координат объекта находят вершины треугольника триангуляции Делоне, в котором находится узел I (рис.1.2).

Значение высоты узла i определяют по формуле:

Z_i = A + BX_i + CY_i (_1.1)

Выражение (_2.1) представляет собой уравнение плоскости проведенной через вершины треугольника, внутри которого находится узел i.

Коэффициенты уравнения (_1.1) A, B и C получают в результате решения системы из трёх уравнений

A + BX + CY ─ Z = 0,

составленных по значениям координат X, Y и высот Z каждой из вершин треугольника.

Цифровое трансформирование снимка выполняется следующим образом.

Сначала формируется прямоугольная матрица цифрового трансформированного изображения, строки и столбцы которой параллельны осям X и Y системы координат объекта, а координаты одного из углов матрицы заданы в этой же системе координат. Размер элементов (пикселей) матрицы обычно выбирают приблизительно равной величине D×m, в которой:

- D - размер пикселя цифрового изображения исходного снимка;

- m - знаменатель среднего масштаба снимка.

Значения координат начала системы координат создаваемой матрицы, выбирают кратными величине элементов матрицы.

Для формирования цифрового трансформированного изображения, каждому элементу цифрового изображения a*_ij необходимо присвоить оптическую плотность изображения соответствующего участка объекта на исходном цифровом снимке. Эта операция выполняется следующим образом. По значениям индексов i и j элементов матрицы a*_ij определяются координаты X, Y центра соответствующего пикселя цифрового трансформированного изображения в системе координат объекта.

По координатам X_i, Y_i точки объекта, соответствующей центру пикселя, по цифровой модели рельефа определяется высота этой точки Z_i.

Определение значения Z_i по ЦМР в виде матрицы высот выполняется методом билинейного интерполирования (рис.1.3).

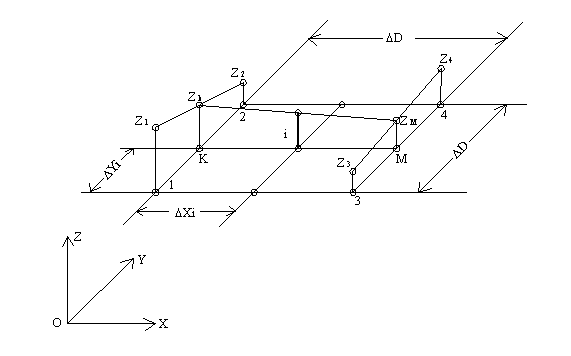
Рис.1.3

На рис.1.3 D X = X_i - X₁, а DY= Y_i - Y₁, где X₁ и Y₁ - координаты узла 1 цифровой модели рельефа.

Высота точки Z_i вычисляется по формуле:

, (1.2)

в которой:

.

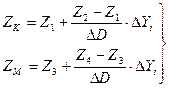По координатам X_i, Y_i, Z_i и значениям элементов внутреннего и внешнего ориентирования снимка вычисляются координаты х,у соответствующей точки на исходном цифровом снимке в системе координат снимка Sхуz.

Вычисления производятся по формулам:

, (1.3)

в которых

.

По координатам х,у и значениям параметров внутреннего ориентирования цифрового изображения определяют координаты точки снимка в системе координат цифрового изображения о_сх_су_с.

В случае использования аффинных преобразований при выполнении внутреннего ориентирования, определение координат выполняется по формулам:

Затем по координатам х_С и у_С вычисляются пиксельные координаты точки

.

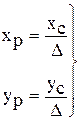По значениям пиксельных координат x_p,y_p точки цифрового изображения снимка, которая является проекцией центра пикселя матрицы цифрового трансформированного изображения, находят ближайшие к этой точке четыре пикселя цифрового изображения снимка. А затем, методом билинейной интерполяции, изложенным в разделе 1.1, по формулам (1.7) определяют значение оптической плотности D_i или цвета соответствующего пикселя матрицы цифрового трансформированного изображения. При этом значение величин Dх_p,Dy_p в формулах (1.7) определяют по формулам:

.

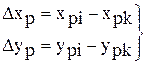Таким же образом определяются оптические плотности или цвет всех остальных пикселей цифрового трансформированного изображения.

Помимо метода билинейной интерполяции для формирования цифрового трансформированного изображения применяют метод “ближайшего соседа”, в котором по пиксельным координатам x_p,y_p находят пиксель цифрового изображения снимка, на который проектируется точка, соответствующая центру пикселя цифрового трансформированного изображения, и значение его оптической плотности или цвета присваивается пикселю цифрового трансформированного изображения.

Метод “ближайшего соседа” позволяет сократить время формирования цифрового трансформированного изображения по сравнению с методом билинейной интерполяции, однако изобразительные свойства формируемого цифрового изображения при этом ухудшаются.

Если превышения точек на участке местности, изображенной на снимке, незначительны, при создании цифрового трансформированного изображения значения высот точек местности, соответствующих центрам пикселей трансформированного изображения, принимаются равными среднему значению высоты участка местности.

В этом случае, нет необходимости в создании цифровой модели рельефа местности, так как трансформированное цифровое изображение представляет собой центральную проекцию исходного снимка на горизонтальную плоскость, расположенную на высоте Z, равной среднему значению высоты участка местности. Такой метод трансформирования допустим в случае, если ошибки в положении точек на трансформированном изображении, вызываемые рельефом местности, не превышают допустимых значений.

Величины максимально допустимых значений превышений точек местности – h _max относительно средней плоскости, при которых ошибки в положении точек на трансформированном изображении не будут превышать установленного допуска DR _max, можно определить по формуле:

h _{max = 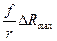, (1. 4)}

в которой:

f – фокусное расстояние съёмочной камеры;

r – расстояние на исходном снимке от главной точки до точки на снимке.

Как следует из формулы 1.4, величина ошибки, DR_max прямо пропорционально значению r. Поэтому при определении h_max измеряется значение r до наиболее удаленной от главной точки снимка точки, участвующей в формировании трансформированного изображения.

Следует отметить, что формулы (1.4) используют только в случае, если трансформирование выполняется по снимкам, углы наклона которых не превышают 3° - 5°.

Аналогичным образом можно определить величину допустимой ошибки Dh_max определения высот точек местности, соответствующих центрам пикселей трансформированного изображения, по цифровой модели рельефа.

Dh_max = 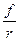DR_max. (1.5)

В случае, если трансформирование снимков выполняется с целью создания или обновления карт и планов значение DR_max выбирается равной величине 0,2 мм на карте или плане. То есть

DR_max = 0.2_мм · M,

где М – знаменатель масштаба создаваемой карты.

При создании цифровых трансформированных изображений местности в проекции карты, плановые координаты узлов цифровой модели рельефа определяют в системе координат карты. В России топографические карты создаются в проекции Гаусса - Крюгера в государственных системах координат СК 42, СК 63 и СК 95.

Высоты узлов цифровой модели рельефа задают равными геодезическим высотам H этих узлов относительно поверхности референц – эллипсоида.

По значениям координат узлов x, y в государственной системе координат вычисляют значения геодезической широты В и долготы L узлов цифровой модели рельефа, а затем по величинам B, L и H, координаты узлов X_гц, Y_гц и Z_гц в геоцентрической системе координат.

Эти преобразования подробно изложены в курсах высшей геодезии и математической картографии.

В остальном, процесс цифрового трансформирования аналогичен процессу создания цифрового ортофотоизображения. Необходимо только отметить, что элементы внешнего ориентирования снимка, в этом случае, должны быть определены в геоцентрической системе координат.

Вместо геоцентрической системы координат можно использовать топоцентрическую систему координат O_тц X_тц Y_тц Z_тц. Начало топоцентрической системы координат обычно выбирают в середине обрабатываемого участка местности. Ось X_тц топоцентрической системы координат лежит в плоскости меридиана, проходящего через начало системы координат. Ось Z_тц совпадает с нормалью к поверхности референц –эллипсоида в начале системы координат, а ось Y_тц дополняет систему до правой. При использовании топоцентрической системы координат, элементы внешнего ориентирования исходного снимка должны быть определены в этой системе координат.

Цифровым фотопланом будем называть цифровое трансформированное изображение местности (объекта) созданное по перекрывающимся исходным снимкам.

Цифровые фотопланы могут быть сформированы из трансформированных изображений, созданных по каждому из перекрывающихся снимков, или путём формирования фотоплана непосредственно в результате трансформирования всех перекрывающихся исходных снимков.

На рис.1.4 представлен принцип формирования цифрового фотоплана по трансформированным изображениям, созданным по каждому из перекрывающихся снимков.

Рис.1.4

Для создания фотоплана используются цифровые трансформированные изображения снимков с одинаковым размером пикселей и имеющие координаты начал систем координат цифровых изображений O₁ и O₂ кратные размеру пикселя.

При создании цифрового фотоплана в зоне перекрытия трансформированных изображений снимков проводят линию пореза в виде полилинии с узлами K_i.

Затем, в каждой строке определяют граничные пиксели, совмещенные с линией пореза, и приступают к формированию матрицы цифрового фотоплана.

Координата начала системы координат цифрового фотоплана X_OM принимается равной наименьшему значению координат X_O1 и X_O2 начал систем координат цифровых трансформированных изображений снимков, а Y_OM – наибольшему значению координат Y_O1 и Y_O2.

Формирование цифрового фотоплана производят следующим образом.

Каждая строка матрицы фотоплана формируется из строки трансформированного изображения снимка P₁, включая граничный пиксель и строки изображения снимка P₂, начиная с пикселя, следующего за граничным.

Описанным выше методом можно присоединить к созданному фотоплану другие перекрывающиеся изображения снимков.

Цифровые фотопланы могут быть созданы путем формирования матрицы цифрового фотоплана непосредственно по всем перекрывающимся цифровым снимкам.

На рис.1. 5 иллюстрируется процесс формирования цифрового фотоплана этим методом.

исходные цифровые снимки

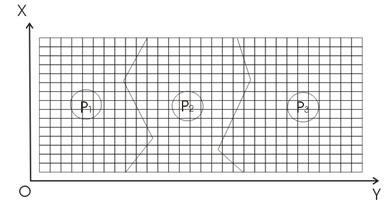
цифровой фотоплан

Рис.1.5

В рассматриваемом методе на перекрывающихся цифровых изображениях снимков проводят линии пореза, которые представляют собой полилинии. По координатам узлов полилинии в системе координат цифрового снимка определяют координаты проекций узлов полилинии на цифровом фотоплане в системе координат объекта и формируют полилинии на цифровом фотоплане.

По этим полилиниям определяют граничные пиксели, которые формируют границы участков цифрового фотоплана, создание которых будет производиться по соответствующим цифровым изображениям снимков.

Формирование цифрового фотоплана в пределах каждого из этих участков производится аналогично процессу формирования цифрового ортофотоснимка, изложенного в разделе 1.2.

Определение координат X,Y узлов полилинии в системе координат цифрового фотоплана по значениям координат x_c, y_c их изображений в системе координат цифрового изображения снимка производится методом приближений следующим образом.

По координатам x_c, y_c изображения узла вычисляются координаты x, y изображения узла в системе координат снимка.

В случае если при внутреннем ориентировании цифрового снимка использовались аффинные преобразования, эти вычисления производятся по формулам:

.

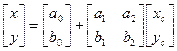Затем вычисляются значения координат X, Y узла в системе координат цифрового фотоплана по формулам:

, (1.6)

в которых

В первом приближении значение высоты узла принимают равной среднему значению высот точек цифровой модели рельефа Z₁.

По вычисленным значениям X₁,Y₁ по цифровой модели рельефа

методом билинейной интерполяции, изложенном в разделе 1.1, определяют уточненное значение высоты узла Z₂. по которому по формулам (1.6) определяют уточненное значение координат узла X₂,Y₂. По координатам X₂, Y₂ узла, в свою очередь, определяют новое значение высоты узла Z₃.

Вычисление продолжают до тех пор, пока разность значений координат X и Y узла в приближениях не будут превышать установленного допуска.

Процесс определения координат X,Y узлов полилинии методом приближений представлен на рис.1.6.

Рис.1.6

Дата добавления: 2015-05-09