Цифровые микросхемы. Типы логики, корпуса

16 + 0 + 4 + 0 + 0.

Путем чрезвычайно сложных расчетов, можно получить сумму этого всего. Она равна 20.

Итак, господа. Только что мы преобразовали двоичное число в десятеричное.
Оказалось, что 101002 = 2010.

Сделать это проще простого, если знать степени двойки. Лично я наизусть с ходу называю все целые степени двойки от 0 до 18. Дальше мне не особо нужно, а если нужно – всегда можно вычислить. А пока что, запомните хотя бы до 16-й:

20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024
211 = 2048
212 = 4096
213 = 8192
214 = 16384
215 = 32768
216 = 65536
и т.д.

Ну теперь давайте преобразуем 8-разрядное двоичное число в десятеричное. Для этого нарисуем такую табличку:

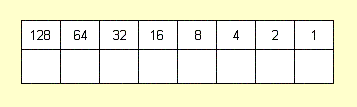
В верхней строчке таблицы – множители, на которые нужно помножать значения разрядов.

Возьмем, к примеру, число 10100111.
Вписываем его в таблицу:

Теперь умножаем значение разряда на множитель этого разряда и складываем результаты:

1*128 + 0*64 + 1*32 + 0*16 + 0*8 + 1*4 + 1*2 + 1*1 =
= 128 + 32 + 4 + 2 + 1 = 167.

Опа! Получилось наше родимое число 167. Чудеса!:)
Все! Преоборазовали!

Посмотрите, что мы в результате сделали. В результате – мы просто сложили множители тех разрядов, в которых стояли едиицы. Такой метод преобразования – самый легкий и простой. И если на уроках информатики вас долго и безрезультатно учили делать кучу операций в столбик – забудьте. Все гораздо проще!

Преобразование 10 ->2

Теперь проделаем то же самое, но – в обратную сторону. Возьмем мы то же самое число 167, и внимательно на него посмотрим. Посмотрели? Теперь посмотрите в таблицу (а лучше - вспомните), какая наибольшая степень двойки еще меньше этого числа.

Очевидно, это 128. Значит, опять рисуем таблицу.

Множитель старшего разряда в ней будет равен 128. Далее – 64, 32, и т.д… Всего – 8 разрядов.

Сразу ставим в старший разряд 1. Дальше станет понятно почему.

Теперь отнимаем от 167 множитель 128.

167 - 128 = 39

Так как 39 меньше следующего множителя (64), в следующий разряд пишем 0.

Так как ничего не отняли – остаток прежний – 39. Смотрим следующий множитель: 32. Он меньше, чем 39, значит его можно отнять. Отнимаем, и ставим в разряд единицу:

Осталось число 7. Оно явно меньше чем 16 или 8, поэтому два следующих разряда будут равны 0:

Дальше:

7 - 4 = 3

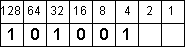
3 - 2 = 1

1 - 1 = 0

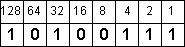
Заметим. В конечном итоге у нас должен получиться НОЛЬ! Если ноль не получился – значит мы где-то напортачили.

Вот. Не смею вас более мучить. Пока что – это все.

Дальше перейдем от теории к практике. Поговорим о микросхемах…

Ну сначала скажем так: микросхемы делятся на два больших вида: аналоговые и цифровые. Аналоговые микросхемы работают с аналоговым сигналом, а цифровые, соответственно – с цифровым. Мы будем говорить именно о цифровых микросхемах.

Точнее даже, мы будем говорить не о микросхемах, а об элементах цифровой техники, которые могут быть «спрятаны» внутри микросхемы.

Что это за элементы?

Некоторые названия вы слышали, некоторые, может быть – нет. Но поверьте, эти названия можно произносить вслух в любом культурном обществе – это абсолютно приличные слова. Итак, примерный список того, что мы будем изучать:

• Триггеры
• Счетчики
• Шифраторы
• Дешифраторы
• Мультиплексоры
• Компараторы
• ОЗУ
• ПЗУ

Все цифровые микросхемы работают с цифровыми сигналами. Что это такое?

Цифровые сигналы– это сигналы, имеющие два стабильных уровня – уровень логического нуля и уровень логической единицы. У микросхем, выполненных по различным технологиям, логические уровни могут отличаться друг от друга.

В настоящее время наиболее широко распространены две технологии: ТТЛ и КМОП.

ТТЛ – Транзисторно-Транзисторная Логика;
КМОП – Комплиментарный Металл-Оксид-Полупроводник.

У ТТЛ уровень нуля равен 0,4 В, уровень единицы – 2,4 В.
У логики КМОП, уровень нуля очень близок к нулю вольт, уровень единицы – примерно равен напряжению питания.

По-всякому, единица – когда напряжение высокое, ноль – когда низкое.

НО! Нулевое напряжение на выходе микросхемы не означает, что вывод «болтается в воздухе». На самом деле, он просто подключен к общему проводу. Поэтому нельзя соединять непосредственно несколько логических выводов: если на них будут различные уровни – произойдет КЗ.

Кроме различий в уровнях сигнала, типы логики различаются также по энергопотреблению, по скорости (предельной частоте), нагрузочной способности, и т.д.

Тип логики можно узнать по названию микросхемы. Точнее – по первым буквам названия, которые указывают, к какой серии принадлежит микросхема. Внутри любой серии могут быть микросхемы, произведенные только по какой-то одной технологии. Чтобы вам было легче ориентироваться - вот небольшая сводная таблица:

	ТТЛ	ТТЛШ	КМОП	Бастродейств. КМОП	ЭСЛ
Расшифровка названия	Транзисторно-Транзисторная Логика	ТТЛ с диодом Шоттки	Комплиментарный Металл-Оксид Полупроводник		Эмиттерно-Согласованная Логика
Основные серии отеч. микросхем	К155 К131	К555 К531 КР1533	К561 К176	КР1554 КР1564	К500 КР1500
Серии буржуйских микросхем		74LS 74ALS	CD40 H 4000	74AC 74 HC	MC10 F100
Задержка распространения, нС	10…30	4…20	15…50	3,5..5	0,5…2
Макс. частота, МГц		50..70	1…5	50…150	300…500
Напряжение питания, В	5 ±0,5	5 ±0,5	3...15	2...6	-5,2 ±0,5
Потребляемый ток (без нагрузки), мА		4...40	0,002...0,1	0,002...0,1	0,4
Уровень лог.0, В	0,4	0,5	< 0,1	< 0,1	-1,65
Уровень лог. 1, В	2,4	2,7	~ U пит	~ U пит	-0,96
Макс. выходной ток, мА			0,5

Наиболее распространены на сегодняшний день следующие серии (и их импортные аналоги):

• ТТЛШ – К555, К1533
• КМОП – КР561, КР1554, КР1564
• ЭСЛ – К1500

Цифровые схемы рекомендуется строить, используя микросхемы только одного типа логики. Это связано именно с различиями в логических уровнях цифровых сигналов.

Тип логики выбирают, в основном, исходя из следующих соображений:

- скорость (рабочая частота)
- энергопотребление
- стоимость

Но бывают такие ситуации, что одним типом никак не обойтись. Например, один блок должен иметь низкое энергопотребление, а другой – высокую скорость. Низким потреблением обладают микросхемы технологии КМОП. Высокая скорость – у ЭСЛ.

В этом случае понадобятся ставить преобразователи уровней.

Правда, некоторые типы нормально стыкуются и без преобразователей. Например, сигнал с выхода КМОП-микросхемы можно подать на вход микросхемы ТТЛ (при учете, что их напряжения питания одинаковы). Однако, в обратную сторону, т.е., от ТТЛ к КМОП пускать сигнал не рекомендуется.

Микросхемы выпускаются в различных корпусах. Наиболее распространены следующие виды корпусов:

DIP
(Dual Inline Package)

Обычный «тараканчик». Ножки просовываем в дырки на плате – и запаиваем.

Ножек в корпусе может быть 8, 14, 16, 20, 24, 28, 32, 40, 48 или 56.

Расстояние между выводами (шаг) – 2,5 мм (отечественный стандарт) или 2,54 мм (у буржуев).

Ширина выводов около 0,5 мм

Нумерация выводов – на рисунке (вид сверху). Чтобы определить нахождение первой ножки, нужно найти на корпусе «ключик».

SOIC
(Small Outline Integral Circuit)

Планарная микросхема – то есть ножки припаиваются с той же стороны платы, где находится корпус. При этом, микросхема лежит брюхом на плате.

Количество ножек и их нумерация – такие же как у DIP.

Шаг выводов – 1,25 мм (отечественный) или 1,27 мм (буржуазный).

Ширина выводов – 0,33...0,51

PLCC
(Plastic J-leaded Chip Carrier)

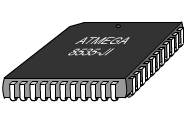Квадратный (реже - прямоугольный) корпус. Ножки расположены по всем четырем сторонам, и имеют J -образную форму (концы ножек загнуты под брюшко).

Микросхемы либо запаиваются непосредственно на плату (планарно), либо вставляются в панельку. Последнее – предпочтительней.

Количество ножек – 20, 28, 32, 44, 52, 68, 84.

Шаг ножек – 1,27 мм

Ширина выводов – 0,66...0,82

Нумерация выводов – первая ножка возле ключа, увеличение номера против часовой стрелки:

TQFP
(Thin Quad Flat Package)

Нечто среднее между SOIC и PLCC.

Квадратный корпус толщиной около 1мм, выводы расположены по всем сторонам.

Количество ножек – от 32 до 144.

Шаг – 0,8 мм

Ширина вывода – 0,3...0,45 мм

Нумерация – от скошенного угла (верхний левый) против часовой стрелки.

Вот так, в общих чертах, обстоят дела с корпусами. Надеюсь теперь вам станет немножко легче ориентироваться в бесчисленном множестве современных микросхем, и вас не будет вгонять в ступор фраза продавца типа: «эта микросхема есть только в корпусе пэ эл си си»…

Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.

Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.

Итак, какие бывают элементы?

Смотрим:

Элемент «И» (AND)

Иначе его называют «конъюнктор».

Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.

Вот так выглядит элемент «И» и его таблица истинности:

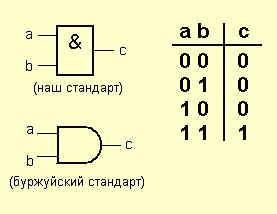
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.

Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.

Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше.

Элемент «ИЛИ» (OR)

По другому, его зовут «дизъюнктор».

Любуемся:

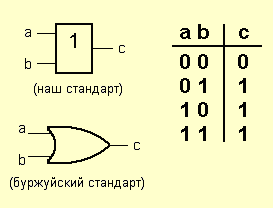
Опять же, название говорит само за себя.

На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.

Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.

Элемент «НЕ» (NOT)

Чаще, его называют «инвертор».

Надо чего-нибудь говорить по поводу его работы?

Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».

Элемент «И-НЕ» (NAND)

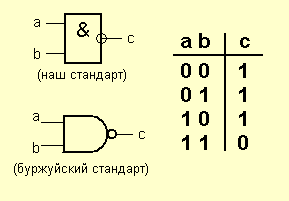
Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» - единица. И наоборот. Э то легко понять по эквивалентной схеме элемента:

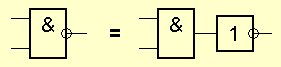
Элемент «ИЛИ-НЕ» (NOR)

Та же история – элемент «ИЛИ» с инвертором на выходе.

Следующий товарищ устроен несколько хитрее:

Элемент «Исключающее ИЛИ» (XOR)

Он вот такой:

Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.

Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый.

Эквивалентная схема примерно такая:

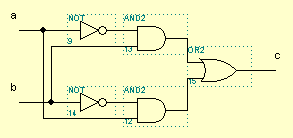
Ее запоминать не обязательно.

Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4.

Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем.

Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питаниеподается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе.

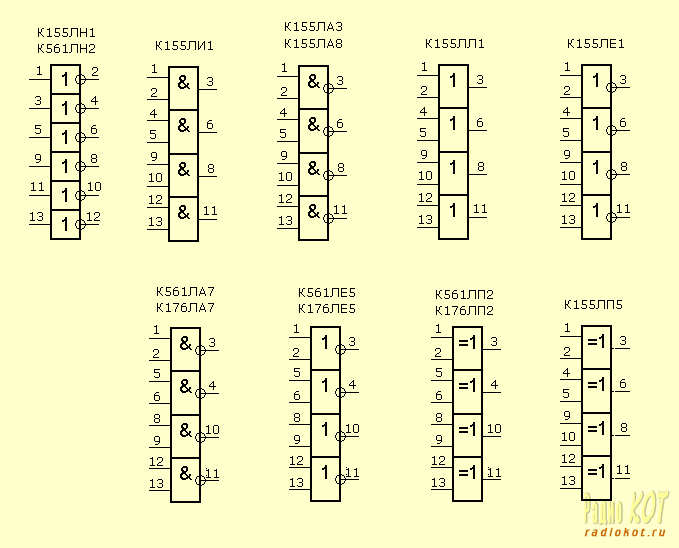
<<--Вспомним пройденное----Поехали дальше->>

РадиоКот > Обучалка > Цифровая техника > Основы цифровой техники

Дата добавления: 2015-05-09