
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В результате получим
|
|
|
|
Для нахождения детекторной характеристики положим
Частотной детектор на цифровой линии задержки
Количество элементов задержки равно K = 2m+1, где m = 1,2...
wn = (-1) m(x n-1 x n-K+1 - x n xn-K).
x n= X0 cos(wnTД).
w = (-1) m X0 2 sin(wTД) sin(w(K-1) TД).
При w = w0 + Dw и w0TД = p/2 получим
w = X0 2 sin(Dw(K-1)TД) cos(DwTД) =
= X0 2 sin(2pDf(K-1)/FД) cos(2pDf/FД).
Обозначим DfN = Df/FД.
Тогда
w(DfN) = X02 sin(2pDfN(K-1)) cos(2pDfN).
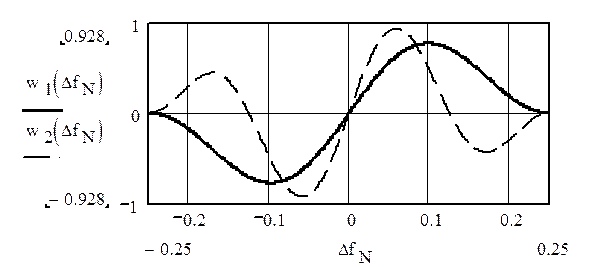
Детекторные характеристики частотного детектора на цифровой линии задержки при K=3 и K=5
Из него видно, что с увеличением K увеличивается крутизна рабочего участка детекторной характеристики, но уменьшается ее раствор, т.е. частотный интервал между двумя экстремальными точками характеристики, ближайшими к DfN= 0.
Коэффициенты второй и третьей гармоник выходного сигнала детектора равны
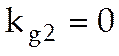 ,
, 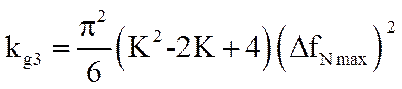 .
.
Коэффициент третьей гармоники выходного сигнала детектора на цифровой линии задержки в  раз больше коэффициента третьей гармоники сигнала на выходе автокорреляционного детектора. Причем с увеличением длины линии задержки искажения увеличиваются.
раз больше коэффициента третьей гармоники сигнала на выходе автокорреляционного детектора. Причем с увеличением длины линии задержки искажения увеличиваются.
Это является недостатком данного детектора.
Его достоинство - простота.
3.9.5. Синхронно-фазовый частотный детектор
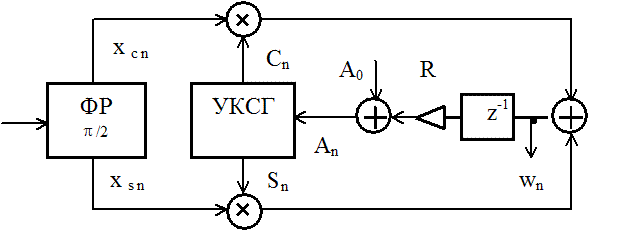
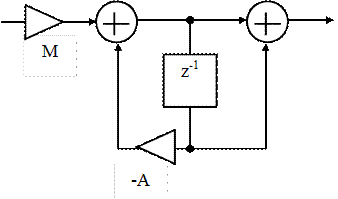
Синхронно-фазовый частотный детектор
Детектор реализуется на кольце фазовой автоподстройки частоты управляемого косинусно-синусного генератора УКСГ по входному частотно-модулированному сигналу.
Управление частотой генератора осуществляется путем изменения переменной An =A0 +Rwn-1.
Константа A0 = 2f0/FД при P=1 задает начальное значение частоты УКСГ при разомкнутом кольце ФАПЧ, равное средней частоте ЧМ сигнала.
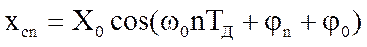 ,
,
 ,
,
где X0 – амплитуда сигнала, w0 = 2pf0, f0 – средняя частота ЧМ сигнала, TД – интервал дискретизации, j0 – постоянная начальная фаза сигнала, jn – мгновенная фаза сигнала, изменяющаяся в процессе модуляции.
Если генератор выполнен на основе генератора пилообразных колебаний, то выходные сигналы генератора определяются следующими соотношениями:
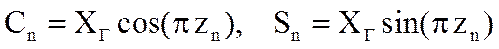 ,
,
где zn – отсчет пилообразного колебания, XГ – амплитуда генерируемых колебаний.
Выходной сигнал детектора равен
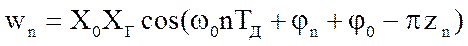 .
.
Обозначим
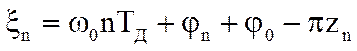 .
.
Найдем разность фаз
 .
.
Учитывая, что
 ,
,
получим
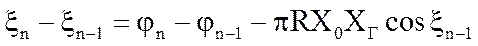 .
.
Последнее соотношение описывает фазовый портрет системы ФАПЧ. При 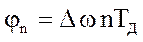 оно преобразуется к виду
оно преобразуется к виду
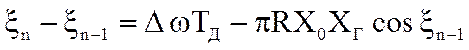 .
.

Фазовый портрет системы ФАПЧ
Из рисунка видно, что синусоида пересекает ось абсцисс.
Белые точки пересечения являются точками устойчивого равновесия системы, т.к. любому увеличению фазы по сравнению со значением в данной точке соответствует отрицательное приращение фазы, что возвращает точку в исходную позицию.
Соответственно уменьшение фазы приводит к положительному приращению.
Черные точки являются точками неустойчивого равновесия.
В точках устойчивого равновесия
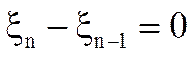 ,
,
Следовательно, выходной сигнал детектора равен
 .
.
Таким образом, выходной сигнал детектора прямо пропорционален отклонению частоты сигнала от ее среднего значения.
Условием устойчивого равновесия системы является наличие точек пересечения синусоиды с осью абсцисс. Из рисунка видно, что это возможно при выполнении неравенства
 ,
,
где  - девиация частоты.
- девиация частоты.
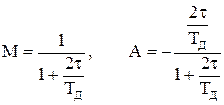
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 690; Нарушение авторских прав?; Мы поможем в написании вашей работы!