Последовательного соединения двух фильтров

Где.

.

Системной функцией цифрового фильтра называется отношение Z-преобразования выходного сигнала фильтра к Z-преобразованию входного сигнала

Воспользовавшись (2.6) и теоремой о дискретной свертке (раздел 2.1), выразим Z-преобразование Y(z) выходного сигнала фильтра y_n через Z-преобразование X(z) входного сигнала x_n

Y(z) = H(z) X(z),

Из последних соотношений следует, что системная функция H(z) представляет собой Z-преобразование импульсной характеристики цифрового фильтра.

Полюсом системной функции называется значение комплексной переменной z, при котором системная функция H(z) стремится к бесконечности.

Нулем системной функции называется значение комплексной переменной z, при котором системная функция H(z) равна нулю.

Рассмотрим формы программной реализации фильтра:

1. Прямая форма

На рисунке 2.5 представлен алгоритм функционирования цифрового фильтра при прямой форме реализации. Прямая форма следует из определения фильтра как линейной системы. Следовательно, n – ый отсчет выходного сигнала фильтра y_n должен быть связан линейными соотношениями с отсчетами входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1,..x_n-N и отсчетами выходного сигнала в предшествующие моменты времени y_n-1, y_n-2,.. y_n-N. Соответствующие коэффициенты пропорциональности B₀, B₁,.. B_N, A₁, A₂,.. A_N определяют свойства фильтра.

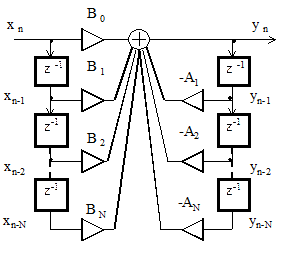
Рисунок 2.5 – Прямая форма программной реализации фильтра

Согласно схеме

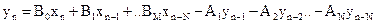. (2.8)

Выразим Z - преобразование выходного сигнала Y(z) через Z-преобразование входного сигнала

Из последнего соотношения получим

. (2.9)

Таким образом, системная функция цифрового фильтра в общем случае представляет собой дробно-рациональную функцию. Полином числителя описывает нерекурсивную часть фильтра, а полином знаменателя – рекурсивную.

Чтобы найти нули системной функции, нужно полином числителя приравнять нулю и найти корни полученного уравнения.

Чтобы найти полюсы системной функции, нужно полином знаменателя приравнять нулю и найти корни полученного уравнения.

Отметим, что знаки перед коэффициентами A в выражении для системной функции и в разностном уравнении (2.8) противоположны.

2.Каноническая форма.

Представим выражение (1.9) в виде произведения двух функций

,

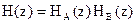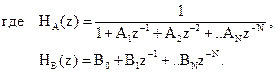(2.10)

Согласно (2.10) цифровой фильтр с системной функцией H(z) можно представить в виде последовательного соединения двух фильтров с системными функциями H_A(z) и H_B(z) (рисунок 2.6).

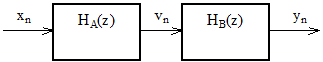
Рисунок 2.6 – Представление фильтра с прямой формой реализации в виде

Действительно,

.

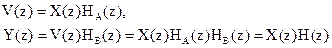Заменив укрупненный алгоритм рисунка 2.6 детальным, получим схему фильтра, изображенную на рисунке 2.7.

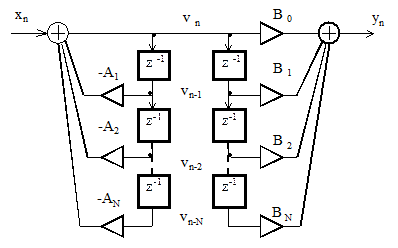
Рисунок 2.7 – Детальный алгоритм представления фильтра с прямой

реализацией в виде последовательного соединения двух фильтров

Из рисунка видно, что для хранения одних и тех же переменных используются две линии задержки, поэтому одну из них можно удалить. При этом схема фильтра преобразуется к виду, представленному на рисунке 2.8. Это и есть каноническая форма программной реализации фильтра.

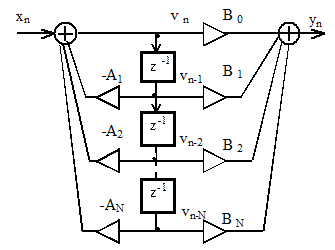
Рисунок 2.8 – Каноническая форма программной реализации фильтра

Достоинством канонической формы является в два раза меньшее количество элементов задержки, следовательно, ячеек памяти вычислительного устройства.

На рисунке 2.8 показана каноническая форма фильтра N-го порядка на одной линии задержки, состоящей из N элементов. Однако обычно вместо структуры, изображенной на рисунке 2.8, используется параллельное или последовательное соединение звеньев второго порядка. Такое представление фильтра связано с возможностью представления системной функции (2.9) в виде произведения или суммы системных функций с полиномами второго порядка в числителе и знаменателе

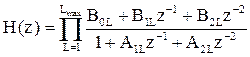, (2.11)

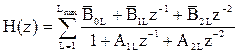, (2.12)

где L – порядковый номер звена, L_max – максимальное значение номера звена

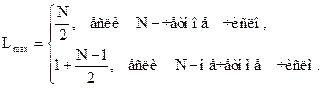
При четном N фильтр состоит из N/2 звеньев второго порядка, при нечетном N фильтр состоит из одного звена первого порядка и (N-1)/2 звеньев второго порядка.

Системная функция звена первого порядка отличается от системной функции звена второго порядка тем, что коэффициенты B₂ и A₂ равны нулю.

Соотношению (2.11) соответствует схема рисунка 2.9а, а соотношению (2.12) – схема рисунка 2.9б.

Рисунок 2.9- Последовательное (а) и параллельное (б) соединение

звеньев фильтра

Типовая схема звена второго порядка приведена на рисунке 2.10. На входе звена показан масштабный коэффициент M_L (как правило, меньше единицы), предотвращающий появление в процессе вычислений значений сигналов фильтра, выходящих за пределы разрядной сетки вычислительного устройства.

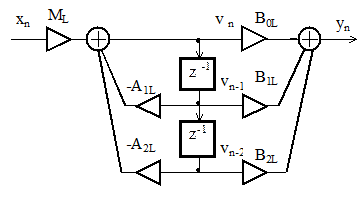
Рисунок 2.9 – Типовое звено второго порядка

2.5.Частотная характеристика цифрового фильтра

Комплексным коэффициентом передачи фильтра 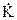является отношение комплексной амплитуды 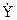выходного сигнала фильтра к комплексной амплитуде входного сигнала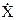

.

Частотной характеристикой цифрового фильтра называется зависимость комплексного коэффициента передачи фильтра от частоты.

Амплитудно-частотной характеристикой (АЧХ) называется зависимость модуля комплексного коэффициента передачи от частоты

.

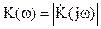Фазочастотной характеристикой (ФЧХ) называется зависимость аргумента комплексного коэффициента передачи фильтра от частоты.

.

Для определения комплексного коэффициента передачи фильтра подадим на вход фильтра с прямой формой реализации (рисунок 1.5) комплексный сигнал с единичной амплитудой

.

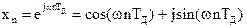Согласно определению комплексного коэффициента передачи комплексный выходной сигнал должен быть равен

.

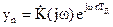Из схемы рисунка 2.5 следует, что выходной комплексный сигнал фильтра определяется следующим соотношением

.

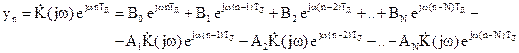Из последнего соотношения получим

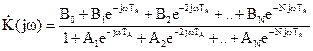(2.13)

Сравнивая последнее соотношение с выражением для системной функции цифрового фильтра, можно сформулировать правило определения комплексного коэффициента передачи при известной системной функции фильтра: для нахождения комплексного коэффициента передачи нужно в выражении для системной функции заменить z на :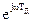

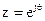, (2.14)

где - нормированная частота – отношение текущей частоты f к частоте дискретизации F_Д.

2.6.Устойчивость цифровых фильтров

Рассмотрим критерии устойчивости цифровых фильтров.

1.Критерий «ОВ-ОВ» («Ограниченный вход – ограниченный выход»)

Цифровой фильтр устойчив, если при ограниченном входном сигнале выходной сигнал фильтра также ограничен.

Условие ограниченности входного сигнала определяется соотношением 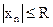, где 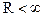, а условием ограниченности выходного сигнала является .

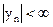Непосредственное использование этого критерия весьма затруднительно, т.к. требует определения значений отсчетов выходного сигнала при всех возможных значениях отсчетов входного сигнала. Поэтому требуются критерии, позволяющие оценить устойчивость фильтра на основании его характеристик.

2.Критерий оценки устойчивости по импульсной характеристике фильтра

В разделе 2.3 было доказано, что выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра

.

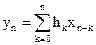Абсолютное значения отсчетов выходного сигнала удовлетворяет неравенству

.

При 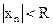справедливо неравенство

.

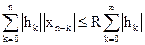Следовательно,

.

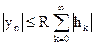Таким образом, чтобы обеспечить выполнение условия 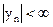, достаточно выполнить условие

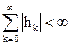. (2.15)

Последнее соотношение определяет критерий устойчивости цифрового фильтра, который формулируется так: цифровой фильтр устойчив, если сумма абсолютных значений отсчетов его импульсной характеристики конечна.

Из этого критерия следует, что все фильтры с конечной импульсной характеристикой абсолютно устойчивы.

В качестве примера воспользуемся критерием (2.15) для проверки устойчивости фильтра, импульсная характеристика которого бесконечна и описывается соотношением

,

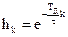где 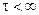– положительная константа, от которой зависит скорость убывания отсчетов импульсной характеристики.

Учитывая, что 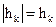, получим

.

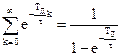Так как 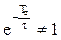, то фильтр устойчив.

3.Критерий оценки устойчивости по системной функции фильтра

В разделе 2.4 показано, что системная функция представляет собой Z-преобразование импульсной характеристики фильтра

.

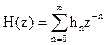Модуль системной функции удовлетворяет неравенству

.

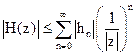При 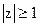справедливо неравенство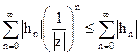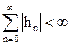

.

При и при 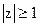модуль системной функции 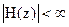. Последнее соотношение означает, что в устойчивом цифровом фильтре должны отсутствовать полюсы системной функции в области комплексной переменной z, которая удовлетворяет неравенству .

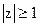Следовательно, если полюсы существуют, то в устойчивом фильтре они должны располагаться в области комплексной плоскости, для которой выполняется условие .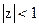

Поэтому критерий устойчивости, связанный с системной функцией фильтра, формулируется следующим образом: цифровой фильтр устойчив, если полюсы системной функции располагаются внутри круга единичного радиуса с центром в начале координат ( ).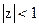

Оценим устойчивость фильтра, системная функция которого описывается соотношением

,

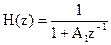где A₁= - 0.5.

Приравняем знаменатель системной функции нулю и определим корень полученного уравнения, который является координатой полюса

.

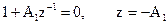На рисунке 2.10 показан круг единичного радиуса и полюс системной функции, располагающийся внутри круга. Следовательно, фильтр устойчив.

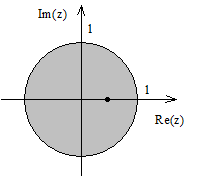
Рисунок 2.10 – Область устойчивости и полюс системной функции

2.7. Коэффициенты системной функции устойчивого звена второго порядка

Системная функция звена второго порядка определяется соотношением

.

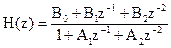Для определения полюсов системной функции приравняем знаменатель нулю и найдем корни полученного квадратного уравнения

Фильтр реализуется в виде звеньев второго порядка в случае комплексно-сопряженных корней, т.е. при

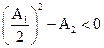. (2.16)

В этом случае корни уравнения определяются следующим соотношением

.

Из последнего соотношения находим

.

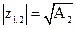Условием устойчивости звена является

.

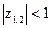Поэтому коэффициент A₂ устойчивого звена второго порядка должен удовлетворять условию

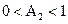. (2.17)

Из неравенств (2.16) и (2.17) следует неравенство для коэффициента A₁

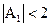. (2.18)

Дата добавления: 2015-05-09