
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общая операция соединения
|
|
|
|
Соединением отношений А и В по условию с назыв отношение 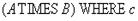
с представляет собой логическое выражение, в которое могут входить атрибуты отношений А и В и (или) скалярные выражения.
Все разновидности соединения являются частными случаями общей операции соединения.
Наиболее важным частным случаем 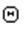 -соединения (equi-join) является случай, когда
-соединения (equi-join) является случай, когда 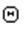 есть просто равенство. Синтаксис экви-соединения:
есть просто равенство. Синтаксис экви-соединения: 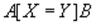
SELECT Orders. OrderID, Orders.CustonerID,
[Order Details].Products
FROM Orders INNER JOIN [Order Details]
ON Orders.OrderID=[Order Details].OrderID WHERE Orders.OrderID=10248;
Формально все соединения являются тета-соединениями. Однако если соединение основано на операторе равенства, его обычно называют эквисоедияением или просто соединением. Соединение, основанное на любом другом операторе сравнения, кроме равенства (<>, >, >=, <, <=) называется тета-соединением.
Для операции 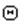 -соединения применяют следующий синтаксис:
-соединения применяют следующий синтаксис: 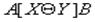
Оператор SELECT, основанный на операторе сравнения «>», позволяет получить список продуктов, лидирующих по продажам в каждой категории:
SELECT DISTINCTROW ProductCategoryAverages.CategoryName,
ProductTotals.ProductName
FROM ProductCategoryAverages INNER JOIN ProductTotals
ON ProductCategoryAverages.CategoryID = ProductTotals.CategoryID AND ProductTotals.TotalSold > [ProductCategoryAverages].[AverageSold];
В реляционной алгебре поддерживается также внешние соединения (outer joins). Внешнее соединение возвращает все записи, которые возвращает внутреннее соединение, плюс все записи из одного или обоих наборов данных, участвующих в соединении. Отсутствующие значения будут замещаться значениями Null.
Внешние соединения, в зависимости от того, какие именно доп-ые записи включены в них, можно разделить на несколько групп: левые, правые, полные.
Левое внешнее соединение (left outer join) возвращает все записи из отношения, находящегося на стороне «один» связи «один ко многим».
SELECT FROM X LEFT OUTER JOIN Y ON <условие>
Правое внешнее соединение (right outer join) – все записи из отношения, находящегося на стороне «многие» такой связи.
SELECT FROM Y RIGHT OUTER JOIN X ON <условие>
Полное внешнее соединение (full outer join) возвращает все записи из обоих наборов, комбинируя те, для которых выполняется условие данного соединения.
SELECT*
FROM X FULL OUTEP JOIN Y ON <условие>
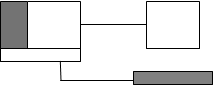 Деление Деление
| Выполняется над двумя отношениями, если набор атрибутов второго отношения (делителя) является подмножеством набора атрибутов первого (делимого). Результат содержит только те атрибуты делимого, которые, во-первых, имеют заданные значения в атрибутах, принадлежащих делителю, и во-вторых, совпадают друг с другом по уникальным атрибутам делимого. |
Реляционное деление возвращает те записи из первого набора, которые совпадают с записями из другого набора.
Отношение 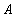 выступает в роли делимого, отношение
выступает в роли делимого, отношение 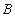 выступает в роли делителя. Деление отношений аналогично делению чисел с остатком.
выступает в роли делителя. Деление отношений аналогично делению чисел с остатком.
Синтаксис операции деления: 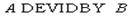
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 909; Нарушение авторских прав?; Мы поможем в написании вашей работы!