Прохождение частицы сквозь потенциальный барьер. Туннельный эффект

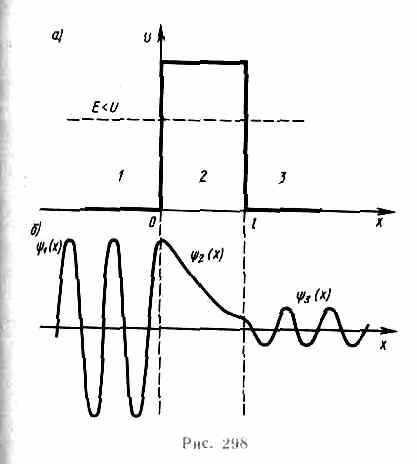
Рассмотрим потенциальный барьер про­стейшей прямоугольной формы (рис. 298, а) для одномерного (по оси х)движения частицы. Для потенциального барьера прямоугольной формы высоты

U и ширины l можем записать

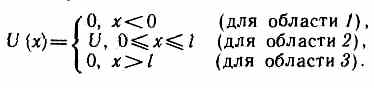
При данных условиях задачи классиче­ская частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при E>U), либо отразится от него (при Е<U) и будет двигаться в обратную сто­рону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же даже при E>U имеется отличная от нуля вероят­ность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<U имеется также отличная от нуля вероятность, что частица окажется в области х>l, т.е. проникает сквозь барьер. Подобные, казалось бы, парадок­сальные выводы следуют непосредственно из решения уравнения Шредингера, опи­сывающего движение микрочастицы при условиях данной задачи.

Уравнение Шредингера (217.5) для стационарных состояний для каждой из выделенных на рис. 298, а области имеет вид

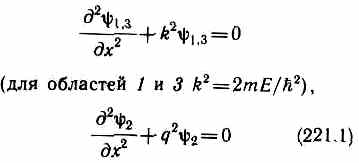
(для области 2q²=2m (E-U}/h²).

Общие решения этих дифференциальных уравнений:

y(x)=A₁e^ikx+B₁e^-ikx (221.2)

(для области 1); y₂ (х)=А₂е^iqx+В₂е^-iqx

(для области 2);

y₃(x)=A₃e^ikx+B₃e^-ikx (221.3)

(для области 3).

В частности, для области 1 полная волновая функция, согласно (217.4), бу-

дет иметь вид

В этом выражении первый член представ­ляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (соответствует части­це, движущейся в сторону барьера), а вто­рой — волну, распространяющуюся в про­тивоположном направлении, т. е. отражен­ную от барьера (соответствует частице, движущейся от барьера налево).

Решение (221.3) содержит также во­лны (после умножения на временной мно­житель), распространяющиеся в обе сто­роны. Однако в области 3 имеется только волна, прошедшая сквозь барьер и рас­пространяющаяся слева направо. Поэтому коэффициент В ₃ в формуле (221.3) следу­ет принять равным нулю.

В области 2 решение зависит от со­отношений E>U или E<U. Физический интерес представляет случай, когда пол­ная энергия частицы меньше высоты по­тенциального барьера, поскольку при E<U законы классической физики одно­значно не разрешают частице проникнуть сквозь барьер. В данном случае, согласно (221.1), q= ib — мнимое число, где

b=Ö(2m (U-E)/h).

Учитывая значение q и В ₃=0, получим решения уравнения Шредингера для трех областей в следующем виде:

y₁(x)=A₁e^ikx + B₁e^-ikx

(для области 1), y ₂(х)=А₂е^-bx+В₂e^bx (221.5) (для области 2),

y ₃(х) =А₃e^ikx (для области 3).

В области 2 функция (221.5) уже не соответствует плоским волнам, распро­страняющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Можно показать, что

для частного случая высокого и широкого барьера, когда b l >>1, В₂»0.

Качественный вид функций y₁(x), y₂(х) и y₃(x) показан на рис. 298, б. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же им­пульсом, т. е. с той же частотой, но с мень­шей амплитудой. Следовательно, получи­ли, что частица имеет отличную от нуля вероятность прохождения сквозь потенци­альный барьер конечной ширины.

Таким образом, квантовая механика приводит к принципиально новому специ­фическому квантовому явлению, получив­шему название туннельного эффекта, в ре­зультате которого микрообъект может «пройти» сквозь потенциальный барьер.

Для описания туннельного эффекта используют понятие коэффициента про­зрачности D потенциального барьера, оп­ределяемого как отношение плотности по­тока прошедших частиц к плотности по­тока падающих. Можно показать, что

D=|A₃|²/|A₁|².

Для того чтобы найти отношение | А ₃ /А ₁|², необходимо воспользоваться условиями непрерывности y и y' на границах барьера х= 0и х=l (рис. 298):

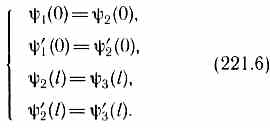
Эти четыре условия дают возможность выразить коэффициенты А ₂, а ₃, В ₁и В ₂ через А ₁. Совместное решение уравнений (221.6) для прямоугольного потенциаль­ного барьера дает (в предположении, что коэффициент прозрачности мал по сравне­нию с единицей)

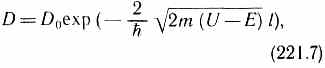
где U — высота потенциального барьера, Е — энергия частицы, l — ширина барь­ера, Do — постоянный множитель, кото­рый можно приравнять единице. Из выражения (221.7) следует, что D сильно зависит от массы m частицы, шири­ны l барьера и от (U-E); чем шире барь­ер, тем меньше вероятность прохождения сквозь него частицы.

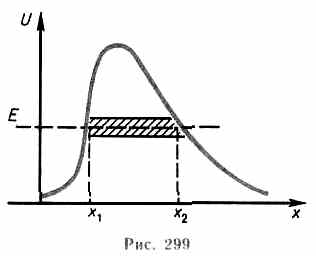
Для потенциального барьера произ­вольной формы (рис.299), удовлетворяю­щей условиям так называемого квазиклас­сического приближения (достаточно глад­кая форма кривой), имеем

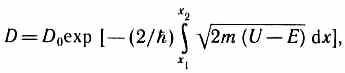
где U=U(x).

С классической точки зрения прохож­дение частицы сквозь потенциальный барьер при E<U невозможно, так как частица, находясь в области барьера, до­лжна была бы обладать отрицательной кинетической энергией. Туннельный эф­фект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может про­никнуть, можно пояснить соотношением неопределенностей. Неопределенность им­пульса D p на отрезке Dx= l составляет D p >h/ l. Связанная с этим разбросом в значениях импульса кинетическая энер­гия (D p)²/(2 m) может оказаться достаточ­ной для того, чтобы полная энергия части­цы оказалась больше потенциальной.

Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. А. Леонтовича (1903—1981). Тун­нельное прохождение сквозь потенциаль­ный барьер лежит в основе многих явле­ний физики твердого тела (например, яв­ления в контактном слое на границе двух

полупроводников), атомной и ядерной фи­зики (например, a-распад, протекание термоядерных реакций).

Дата добавления: 2015-05-09