Цифровой

Преобразование аналогового телевизионного сигнала в

План (логика) изложения материала

Экспресс - проверка знаний пройденного материала

Лекция 27

Вопросы для самостоятельной работы

1 Что такое цифровое телевидение?

2 Какие преимущества может обеспечить цифровое телевидение?

3 Назовите основные этапы развития цифрового телевидения.

4 Какие международные организации утверждают стандарты и рекомен­дации в

области телевидения?

5 Что означают аббревиатуры "JPEG" и "MPEG"?

6 Каковы назначения кодера источника и кодера канала в цифровой
телевизионной системе?

Литература

1 Джакония В.Е. и др. Телевидение: Учебник для вузов; под ред. В.Е.

Джаконии 4-ое изд. Стереотип. – М.: Горячая линия- Телеком, 2007. -616

с. 82…84.

2 Смирнов А.В. Основы цифрового телевидения: Учебное пособие.- М.:

«Горячая линия - Телеком», 2001.-224с.: с.5….12.

1 Нарисовать обобщенную структурную схему передающей цифровой системы

2 Нарисовать обобщенную структурную схему приёмной цифровой системы

После изучения лекции № 27 студент должен знать: принцип преобразования аналогового телевизионного сигнала в цифровой

Уметь: нарисовать временные диаграммы преобразования сигнала из аналоговой формы в цифровую

3.2.3 Преобразование аналогового телевизионного сигнала в

цифровой

Цифровой телевизионный сигнал получается из аналогового телевизионного сигнала путем преобразования его в цифровую форму. Это преобразование включает следующие три операции:

1 Дискретизацию во времени, т. е. замену непрерывного аналогового

сигнала последовательностью его значений в дис­кретные моменты

времени - отсчетов или выборок.

2 Квантование по уровню, заключающееся в округлении значения каждого

отсчета до ближайшего уровня квантования.

3 Кодирование (оцифровку), в результате которого значение отсчета

представляется в виде числа, соответствующего номеру полученного

уровня квантования.

Все три операции выполняются в одном узле - аналого-цифровом

преобразователе (АЦП). В современной аппаратуре АЦП реализуется в виде одной БИС. На входы АЦП (рисунок 3.59) подаются аналоговый сигнал u{t) и тактовые импульсы Cт, син­хронизирующие моменты выборок. Выходные сигналы d...d„ об­разуют параллельный n -разрядный двоичный код,

представляю­щий получающееся в результате аналого-цифрового

преобразова­ния число.

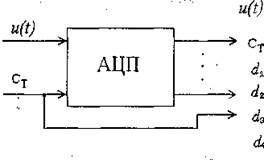
Рисунок 3.59 - Схема включения АЦП

Дискретизация — замена непрерывного аналогового ТВ сигна­ла u(t)

последовательностью отдельных во времени отсчетов это­го сигнала. Наиболее распространена равномерная дискретизация, имеющая постоянный период, основанная на теореме Котельникова-Найквиста. Согласно этой теореме любой непрерывный сигнал u(t), имеющий ограниченный спектр частот (рисунок 3,а), может быть пред­ставлен значениями этого сигнала u{t_n), взятыми в дискретные мо­менты времени (отсчеты) t_n = пТ (рисунок 3 ,6), где п = 1,2,3,... — целые числа; Т — период или интервал дискретизации, выбранный из условия теоремы Котельникова-Найквиста: Т = 0,5/f_гр. Здесь f_гр — максимальная частота спектра исходного сигнала u(t). Величина, обратная периоду дискретизации, называется частотой дискрети­зации. Минимально допустимая частота дискретизации

f_д = 2/_гр.

Рисунок 3. 60 - Преобразование сигнала из аналоговой формы в цифровую

Аналитическое выражение теоремы Котельникова-Найквиста име­ет вид

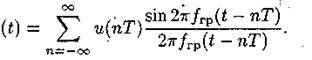
Предполагается, что отсчеты u(пТ) являются δ -импульсами (бесконечно короткими). Для восстановления исходного аналогового сигнала u(t ) из последовательности отсчетов u(пТ ) последние необ­ходимо в соответствии с пропустить через идеальный фильтр нижних частот (ФНЧ) со срезом на частоте f_гр.

Множитель [sin 2πf_rp(t — nT)] / 2πf_rp(t — пТ)] представляет собой реакцию такого фильтра на единичный импульс u(пТ ). Из теоре­мы следует, что для точного восстановления исходного сигнала необходимо наличие бесконечно большого числа отсчетов. На практи­ке же сигнал, всегда имеющий конечную длительность, описывается конечным числом отсчетов. Несмотря на несоответствие условиям теоремы, такой способ восстановления сигнала широко используется в цифровом телевидении, и точность восстановления при соблюдении определенных требований оказывается достаточной.

За процессом дискретизации при преобразовании аналогового сигнала в цифровую форму следует процесс квантования.

Кванто­вание (этот термин заимствован из атомной физики) заключается в замене полученных после дискретизации мгновенных значений отсче­тов ближайшими значениями из набора отдельных фиксированных уровней

(рисунок 3.60,в). Квантование также представляет собой дискре­тизацию ТВ сигнала, но осуществляемую не во времени, а по уровню сигнала u(t). Для устранения путаницы между этими понятиями и введена разная терминология.

Фиксированные уровни, к которым «привязываются» отсчеты, называют уровнями квантования. Разбивая динамический диапазон изменения сигнала u(t ) уровнями квантования на отдельные области значений, называемые шагами квантования, образуют шкалу кван­тования. Последняя может быть как линейной, так и нелинейной, в зависимости от условий преобразования. Округление отсчета до одного из двух ближайших уровней (верхнего или нижнего) опреде­ляется положением порогов квантования (рисунок 3.60,е).

Возможность восстановления в зрительном аппарате человека исходного изображения по его квантованному приближению (в теоре­ме эта операция не предусматривается) вытекает из ограниченности контрастной (и цветовой) чувствительности зрительной системы.

Строго говоря, дискретизированный и квантованный сигнал u_кв(пТ ) уже является цифровым. Действительно, если амплиту­да импульсов дискретизированного сигнала u(пТ ) может принимать любые произвольные значения в пределах исходного динамического диапазона сигнала u(t ), то операция квантования привела к замене всех возможных значений амплитуды сигнала ограниченным числом значений, равным числу уровней квантования. Таким образом, кван­тованная выборка сигнала выражается некоторым числом в системе счисления с основанием m, где m — число уровней квантования. Но цифровой сигнал в такой форме по помехозащищенности мало выигрывает по сравнению с аналоговым, особенно при большом m. Для увеличения помехозащищенности сигнала его лучше всего пре­образовать в двоичную форму, т.е. каждое значение уровня сигнала записать в двоичной системе счисления. При

этом номер (значение уровня) будет преобразован в кодовую комбинацию

символов 0 или 1 (рисунок 3.60,г). В этом и состоит третья, заключительная операция по преобразованию аналогового сигнала u(t) в цифровой, называе­мая операцией кодирования.

Кодирование представляет собой преобразование квантованного значения отсчета u_кв(пТ ) несоответствующую ему кодовую комбина­цию символов u_ц(nТ); Наиболее распространенный способ кодиро­вания ТВ сигнала — представление его дискретных и проквантованных отсчетов в натуральном двоичном коде. Этот способ получил название импулъсно-кодовой модуляции ( ИКМ ). На рисунок 3,г пока­зан результат преобразования фрагмента исходного сигнала u(t) в последовательность комбинаций двоичного трехразрядного кода.

Часто всю совокупность перечисленных операций — дискрети­зации, квантования и кодирования для краткости называют кодиро­ванием телевизионного сигнала. Это имеет определенные техниче­ские основания, поскольку все эти три операции выполняются од­ним техническим устройством — аналого-цифровым преобразовате­лем (АЦП). Обратное преобразование цифрового сигнала в аналого­вый производится в устройстве, называемом

цифро-аналоговым пре­образователем (ЦАП). Аналого-цифровые и цифро-аналоговые пре­образователи — непременные блоки любых цифровых систем пере­дачи, хранения и обработки изображений.

Исследования ИКМ в телевидении начались сравнительно давно. Первые предложения относятся еще к 30 -м годам. Но только недавно этот метод стал применяться в вещательном телевидении. Причина столь длительного внедрения объясняется жесткими требованиями к быстродействию устройств преобразования и передачи цифрового сигнала. Чтобы пояснить это, оценим скорость передачи цифрового потока ИКМ сигнала по каналу связи.

ІІри непосредственном кодировании телевизионного сигнала ме­тодом ИКМ кодовые комбинации создаются с частотой, равной ча­стоте отсчетов, т.е. частоте дискретизации. Каждая кодовая комби­нация соответствует определенному отсчету и содержит некоторое число k двоичных символов (битов).

Скоростью цифрового потока с называется число передаваемых двоичных знаков в единицу времени. За единицу скорости принима­ется 1 бит в секунду. Таким образом, скорость передачи ТВ сигнала в цифровой форме равна произведению частоты дискретизации f_д и числа двоичных символов k в одном дискретном отсчете:

с = f _д × k. (3.1)

Для количественной оценки скорости передачи ИКМ сигнала не­обходимо обосновать выбор k и f_д. Число двоичных символов k в кодовой комбинации одного отсчета связано с числом уровней кван­тования m исходного сигнала соотношением

k = log₂m ≈ 3, 31 lg m. (3.2)

Выбор числа уровней квантования определяется требованием к минимизации ошибок (ошибок квантования), возникающих из-за замены истинных значений отсчетов сигнала их квантованными (при­ближенными) значениями. Ошибки

квантования носят случайный характер. Поэтому искажения, вызываемые этими ошибками, часто называют шумами квантования. На изображении они могут про­являться по-разному, в зависимости от свойства кодируемого сигна­ла. Если собственные шумы аналогового сигнала невелики по срав­нению с шагом квантования, то шумы квантования проявляются на изображении в виде ложных контуров. Такие искажения хорошо заметны при «грубом» квантовании, когда число уровней квантова­ния недостаточно. В этом случае плавные яркостные переходы пре­вращаются в ступенчатые. Наиболее заметны ложные контуры на изображениях с крупными планами. Этот эффект усугубляется на подвижных изображениях. Эксперименты показывают, что ложные контуры перестают восприниматься, если число уровней квантова­ния превышает 100-200, т.е. шум квантования не превышает 0,5_…1 % размаха сигнала. Эти данные хорошо согласуются с понятиями о контрастной чувствительности зрения.

Если собственные шумы аналогового сигнала достаточно велики и превышают шаг квантования, то искажения квантования проявля­ются уже не как ложные контуры, а как шумы, равномерно рас­пределенные по спектру. Флуктуационные помехи исходного сигна­ла как бы подчеркиваются, изображение в целом начинает казать­ся более зашумленным.

Недостаточное число уровней квантования особенно неприятно сказывается на цветных изображениях. Шумы квантования про­являются в виде цветных узоров, особенно заметных на таких сю­жетах, как лицо крупным планом, на плавных перепадах яркости и пр. В настоящее время рекомендуется использование линейной де­сятиразрядной шкалы квантования, предусматривающей квантова­ние соответственно на 1024 уровня. Хотя еще несколько лет назад считалось вполне удовлетворительным квантование на 256 уровней (восьмиразрядной шкалой).

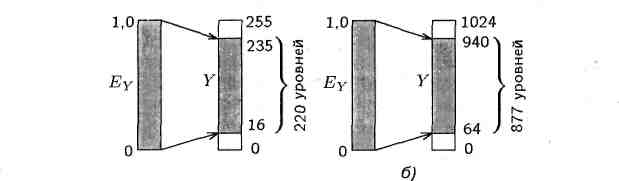
На рисунке 3.61 приведены диаграммы, дающие представление о соот­ветствии между аналоговым сигналом яркости Еу и уровнями квантования для восьми -

а)

а — восьмиразрядная шкала; 6— десятиразрядная шкала

Рисунок 3.61- Соответствие размаха яркостного аналогового сигнала шкале

кван­тования

и десятиразрядной шкалы. В восьмиразряд­ной шкале сигналу отводится 220 уровней квантования (с 16 -го, со­ответствующего уровню черного, по 235 -й,

соответствующий белому). В десятиразрядной шкале яркостный сигнал

квантуется на 877 уров­ней (64 -й соответствует уровню черного, а 940 -й — уровню белого). Из неиспользуемых уровней одна часть резервируется для цифровых синхронизирующих сигналов, другая — представляет собой рабочий запас на возможные в процессе преобразования аналогового сигна­ла превышения им допустимого диапазона значений. Подобные слу­чаи для аналоговой техники весьма вероятны, а связанные с этим перегрузки аналогово-цифровых преобразователей приводили бы к заметным неустранимым искажениям в изображении.

Рассмотрим теперь факторы, определяющие выбор частоты дис­кретизации. Дискретизация — первая операция из всего комплекса преобразований аналогового сигнала в цифровой. Исходный сигнал u(t ) после дискретизации можно представить в виде суммы:

∞

u(nТ) = ∑ u(t)δ(t-nT ), (3.3)

n = -∞

где δ — дельта-функция; Т — период дискретизации.

Если (5.4) подвергнуть преобразованию Фурье, то

∞

S(f) = ∑ S(f - nf_д ), (3.4)

n = -∞

где S(f) и S(f_д) — спектры исходной и дискретизированной функ­ций соответственно.

Из (3.4) следует, что спектр дискретизированного сигнала пред­ставляет собой сумму исходного спектра (n = 0) и «побочных» или
дополнительных спектров того же вида, но сдвинутых один относи­тельно другого на fд, 2fд,... и т.д. (рисунок 3.62). Из рисунка видно, что
с помощью идеального фильтра нижних частот (ФНЧ) с частотой
среза (ФНЧ) можно выделить спектр исходного сигнала, если выпол­няются условия:

1) fд ≥ 2 fг_Р; 2) f_гр ≤ f_фнч ≤ f_д - fг_Р.

Если же частота отсчетов выбрана из условия f_д < 2f_гр, то по­сле дискретизации побочные спектры будут перекрывать основной (рисунок 3.63), и восстановить исходный сигнал без помех невозможно.

Таким образом, при полосе частот яркостного сигнала, рав­ной 6 МГц, частота дискретизации должна быть выбрана не менее 12 МГц. Учитывая невозможность создания фильтра нижних частот с прямоугольной АЧХ, эта цифра должна быть несколько увеличена.

На выбор частоты дискретизации влияют также следующие об­стоятельства. Изображение, подвергнутое кодированию, представля­ет собой совокупность отсчетов (пикселей), структура которых зависит от частоты дискретизации. Лучшие результаты достигаются при фиксированной относительно телевизионного растра структуре отсчетов, расположенных в узлах

прямоугольной решетки — так на­зываемая ортогональная структура

дискретизации (рисунок 3.64). Для этого необходимо, чтобы частота дискретизации была кратной часто­те строк. Кроме того, желательно удовлетворение этому требованию одновременно для двух мировых стандартов разложения: 625/50 и 525/60. Одним из вариантов, отвечающих этим условиям, является частота

13,5 МГц. В этом случае видимая часть строки изображения для обоих стандартов состоит из 720 пикселей, что примерно соот­ветствует разрешению аналогового вещательного телевидения. Для более высокого формата разрешения частота дискретизации должна быть пропорционально увеличена.

Приняв во внимание параметры квантования и дискретизации аналогового телевизионного сигнала, оценим скорость цифрового по­тока яркостного сигнала для k = 10 и fд = 13,5 МГц:

с = 10 • 13,5 = 135 Мбит

А если учесть, что кроме сигнала яркости должна быть переда­на информация о цвете, то общий цифровой поток, формируемый по методу ИКМ, удвоится и будет равен 270 Мбит/с. Столь высоким быстродействием должны обладать как устройства преобразования ТВ сигнала, так и каналы связи. Очевидно, нельзя считать экономи­чески целесообразной передачу такого большого цифрового потока по каналам связи. Важной задачей для построения более экономичных ТВ систем является сжатие или компрессияТВ сообщения.

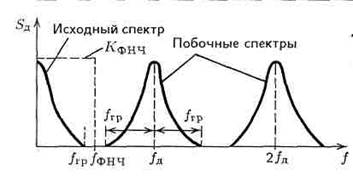
Рисунок 3.62 - Спектр сигнала после дискретизации

Рисунок 3.63 - Перекрытие спектров при f_д < 2 f_гр

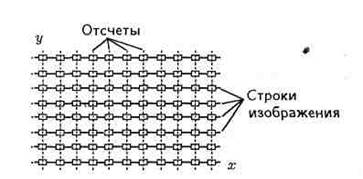
Рисунок 3.64 - Ортогональная структура дискретизации

Дата добавления: 2015-05-09