Лабораторная работа № 2. Методы криптографии. Генерация псевдобесконечных ключей на основе датчиков псевдослучайных чисел

Цель работы

Лабораторная работа № 1. МЕТОДЫ КРИПТОГРАФИИ. ПОДСТАНОВКИ

Тула 2000

Методические указания

По выполнению лабораторных работ для студентов дневного обучения по направлению 552800 «Информатика и вычислительная техника» специальности 220100 «Вычислительные машины, комплексы, системы и сети»

Содержание

Лабораторная работа № 1. МЕТОДЫ КРИПТОГРАФИИ. ПОДСТАНОВКИ....................................................................................... 3

Лабораторная работа № 2. МЕТОДЫ КРИПТОГРАФИИ. ГЕНЕРАЦИЯ ПСЕВДОБЕСКОНЕЧНЫХ КЛЮЧЕЙ НА ОСНОВЕ ДАТЧИКОВ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ............................................................ 8

Лабораторная работа № 3. МЕТОДЫ ДВУХКЛЮЧЕВОЙ КРИПТОГРАФИИ................................................................................... 11

Лабораторная работа № 4. МЕТОДЫ КРИПТОГРАФИИ. РЕАЛИЗАЦИЯ ПРОЦЕДУР СТАНДАРТА DES............................................................. 16

Лабораторная работа № 5. МЕТОДЫ КРИПТОГРАФИИ. РЕАЛИЗАЦИЯ РЕЖИМОВ СТАНДАРТА DES............................................................. 28

Лабораторная работа № 6. МАКРОСЫ ДОКУМЕНТОВ MS WORD. ПРОЕКТИРОВАНИЕ МАКРОСОВ. ПРОБЛЕМЫ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ................................................................................... 33

Лабораторная работа № 7. МЕТОДЫ ПРОЕКТИРОВАНИЯ ПО ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ НА ОСНОВЕ ТЕХНОЛОГИИ ВИЗУАЛЬНОГО ПРОГРАММИРОВАНИЯ........................................ 39

ЛИТЕРАТУРА......................................................................................... 48

Знакомство с методами подстановок в криптографии. Получение навыков шифрования и дешифрования сообщений, а также разработки соответствующего программного обеспечения на основе технологии визуального программирования.

2. Теоретические положения

Пример шифрования: шифр Цезаря

Очень простым примером преобразования секретной информации является шифр Цезаря, который по имеющимся свидетельствам, был использован Юлием Цезарем. Первая строка знаков табл. 1 есть зашифрованная форма сообщения, представленного второй строкой знаков таблицы (Для лучшего катания на лыжах нужно больше снега).

Таблица 1.

Шифр Цезаря практически представляет собой частный случай метода моноалфавитной подстановки букв одного алфавита. Каждый знак P из исходного алфавита заменяется соответствующим числом b(P) [b(A) = 1, b(B) = 2,..., b(пробел) = 0]. Затем формируется эквивалентное зашифрованное число g по выражению (1)

g(P) = b(P) + 2 (mod 27). (1)

Таким образом, g(T) = b(T) + 2 = 20 + 2 = 22, g(I) = b(I) + 2 = 9 + 2 = 11 и т. д.

Значения g замещаются соответствующими им буквами для получения зашифрованного текста. Фактически шифр Цезаря – это любой шифр в форме C = P + K (mod 27), где 1 £ K £ 26, а исходным алфавитом является

ABCDEFGHIJKLMNOPQRSTUVWXYZb

(b соответствует знаку пробел).

В более общей форме в криптографической системе исходное сообщение M и ключ K являются входами в некоторое преобразующее устройство, которое может быть реализовано или аппаратно, или программно.

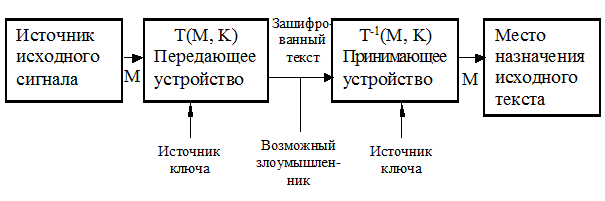
Рис. 1. Криптографические системы

Прямые подстановки

В прямых подстановках каждый знак исходного текста заменяется одним или несколькими знаками. Одним из важных подклассов прямых подстановок являются моноалфавитные подстановки, в которых устанавливается взаимоодназначное соответствие между каждым знаком a_i алфавита сообщений A и соответствующим знаком h_j зашифрованного текста. Рассмотрим пример шифрования методом подстановки:

Исходное сообщение: WE NEED MORE SNOW FOR BETTER SKIING

Ключ:

Вход:	BABCDEFGHIJKLMNOPQRSTUVWXYZ
Выход:	VZHLANQRCWDXFOUSPBTIELGMbKY

Шифровка: MNVUNNAVOSTNVIUSMVQSTVHNEENTVIXWWUR (2)

Зашифрованное сообщение (2) получается следующим образом. Берется очередной знак из исходного сообщения. Определяется его порядковый номер в строке «Вход» ключа. В зашифрованное сообщение вставляется символ из строки «Выход» ключа, с тем же порядковым номером.

Этот метод подстановки хотя до некоторой степени и является эффективным для введение в заблуждение при случайном прочтении, не сможет надолго остановить специалиста, поскольку он легко поддается осуществляемому с помощью ЭВМ частотному анализу встречаемости букв и пар букв (будет рассмотрен ниже).

Все методы моноалфавитной подстановки можно представить как числовые преобразования кодов букв исходного текста. Каждый код буквы в тексте умножается на некоторое число (называемое десятичным коэффициентом) и прибавляется к некоторому другому числу (коэффициенту сдвига)

c = a · P + s (mod K), (3)
где a – десятичный коэффициент; s – коэффициент сдвига; K – размер алфавита. Нетрудно убедится, что уравнение (1) является фактически уравнением (3) с a = 1, s = 2 и K = 27.

Многоалфавитные подстановки

Простая многоалфавитная подстановка последовательно и циклически меняет используемые алфавиты. При u-алфавитной подстановке знак m₁ из исходного сообщения заменяется знаком из алфавита B₁, знак m₂ – соответствующим из алфавита B₂,..., m_u – знаком из алфавита B_u, m_u+1 – снова из алфавита B₁ и т. д.

Входной символ:	m1	m2	m3	m4	m5	m6	m7	m8	m9	...
Алфавит подстановки:	B1	B2	B3	B4	B1	B2	B3	B4	B1	...

Эффект использования многоалфавитной подстановки состоит в том, что обеспечивается маскировка естественной частотной статистики исходного языка L, так как конкретный знак из алфавита A может быть преобразован в несколько различных знаков шифровальных алфавитов B_j.

G-контурная многоалфавитная подстановка

G-контурная многоалфавитная подстановка представляет собой метод шифрования, использующий g наборов алфавитов, применяемых циклически с периодами u₁, u₂,..., u_g. Каждый j-й зашифрованный знак получается из выражения

,
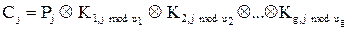где Ä – некоторая обратимая операция. Этот шифр раскрыть сложнее, чем простую многоалфавитную подстановку.

Монофонические шифры

Монофонический шифр представляет собой многоалфавитный шифр подстановки, уравнивающий частоту появления зашифрованных знаков и таким образом защищающий шифр от раскрытия с помощью частотного анализа. Для знаков встречающихся часто, требуется относительно большое число зашифрованных эквивалентов. В то же время для нечасто используемых исходных знаков может оказаться достаточным один или два зашифрованных знака. При реализации этого криптографического метода приходится увеличивать разрядность представления кодов символов в алфавитах подстановки. Для монофонических шифров существуют аппаратные средства криптографии.

Общие принципы для методов шифрования подстановкой

Все описанные методы шифрования можно рассматривать как задачи современной алгебры. Между K знаками алфавита A и набором положительных чисел 0, 1,..., K - 1 устанавливается произвольное соответствие. При сложении и вычитании по модулю K эти положительные числа формируют алгебраическое кольцо, используемое для шифрования, а также однозначные обратные преобразования. Поэтому если мы выбираем целое w в диапазоне от 0 до K - 1, то этим самым автоматически производим выбор конкретного преобразования подстановкой e_i = m_i + w (mod K) и обратного преобразования m_i = e_i - w (mod K). Если w фиксировано, то мы имеем одноалфавитную подстановку. Если w выбирается из последовательности w₁, w₂,..., w_n, то мы имеем многоалфавитную подстановку с периодом n.

Если в многоалфавитной подстановке

1) число знаков в ключе превышает общее число шифруемых знаков;

2) ключ используется только один раз;

3) исходный текст не может быть похищен злоумышленником,

то зашифрованный текст является теоретически нераскрываемым и называется системой Вермана. Поэтому всегда следует стремиться к длинным наборам знаков ключа. Существуют методы, позволяющие получать бесконечные ключевые последовательности, которые могут быть использованы во многих приложениях.

3. Задание на работу

Разработать программу шифрования текста с помощью шифра указанного в задании (величина смещения по алфавиту должна задаваться пользователем). Зашифровать любой текст достаточного объема (несколько тысяч знаков). Получить таблицу встречаемости символов алфавита в данном тексте.

В интегрированной среде программирования разработать программное обеспечение для автоматизированной дешифрации (взлома) зашифрованного текста, при условии, что способ шифрования известен, а ключ – нет.

Варианты:

1) Шифр Цезаря.

2) Прямые подстановки.

3) Многоалфавитная подстановка

4) G-контурная многоалфавитная подстановка

5) Монофонический шифр

4. Оборудование

ПЭВМ с архитектурой IBM PC, операционная система – Windows 95, интегрированная среда – C++ Builder или Delphi версии не ниже 3.0

5. Порядок выполнения работы

1) Согласно полученному варианту задания разработать и отладить ПО для автоматизированной дешифрации предложенного файла с текстом.

2) Расшифровать предложенный файл с текстом.

3) Оформить отчет.

6. Оформление отчета

Отчет должен содержать:

− задание на лабораторную работу;

− листинг разработанного ПО для автоматизированной дешифрации предложенного файла с текстом;

− расшифрованный текст.

7. Контрольные вопросы

1) В каком случае в качестве эффективного метода взлома ключа целесообразно использовать частотный анализ?

2) Что такое шифр Цезаря?

3) Что понимают под прямыми подстановками?

4) В чем заключаются многоалфавитные подстановки?

5) Укажите особенности G-контурной многоалфавитной подстановки.

6) Что такое монофонические шифры?

7) Сформулируйте общие принципы для методов шифрования подстановкой.

Дата добавления: 2015-05-07