
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контактное термическое сопротивление
|
|
|
|
Б) Теплопроводность через многослойную плоскую стенку.
А) Теплопроводность через однослойную плоскую стенку
Коэффициент теплопроводности
Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4) 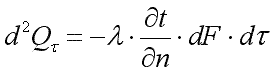 .:
.:
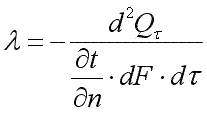 . .
| (9.8) |
Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных.
Плотность теплового потока находится из уравнения Фурье:

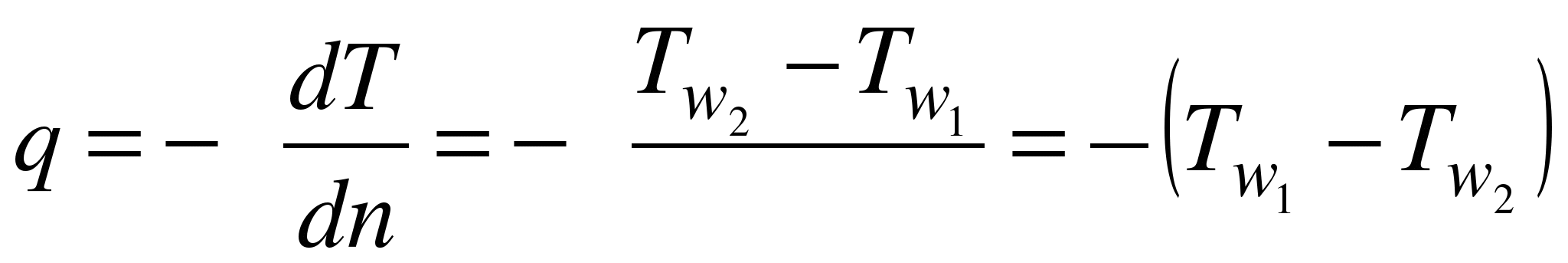 ,
, 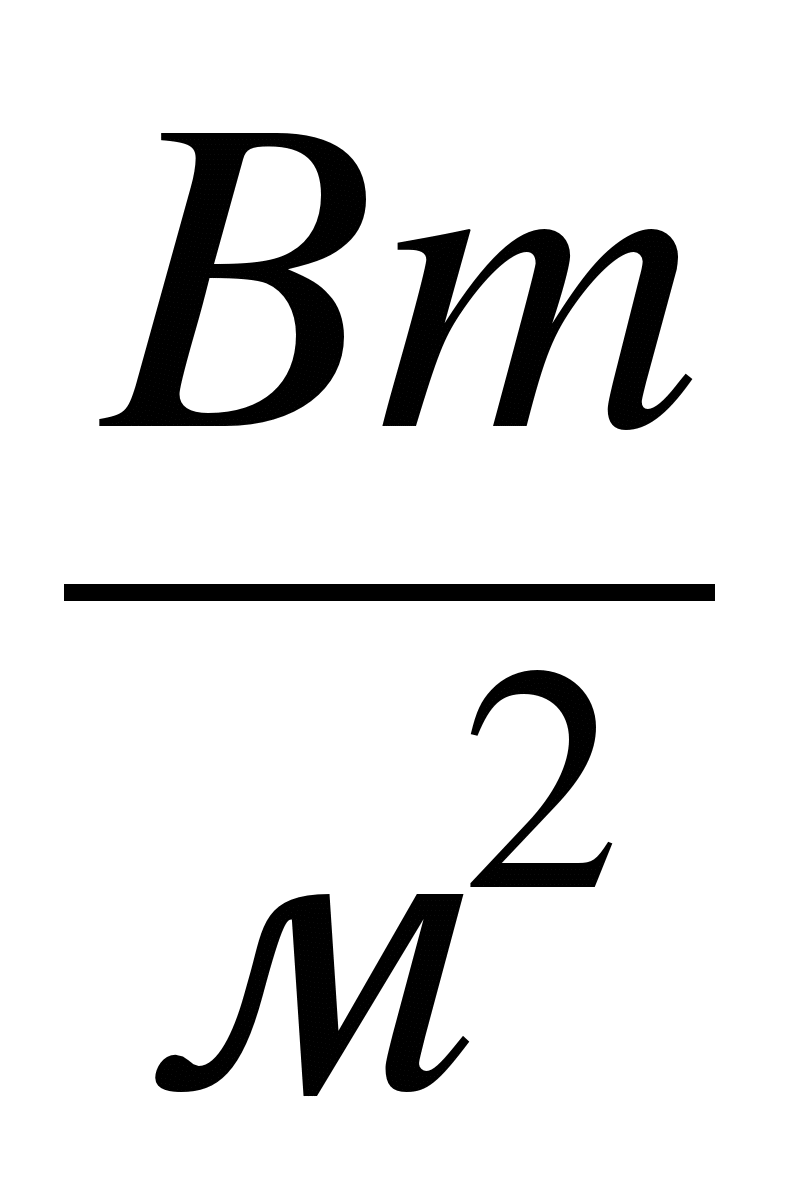 .
.
Общее количество теплоты, которое передается через поверхность стенки 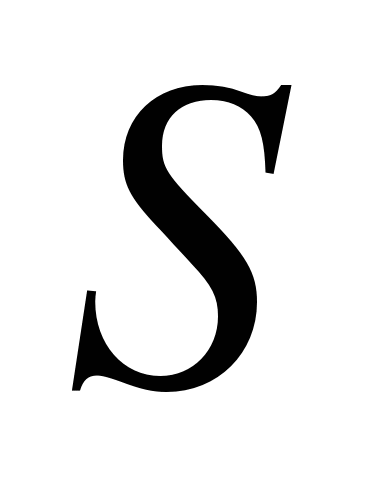 за время
за время  :
:
 ,
, 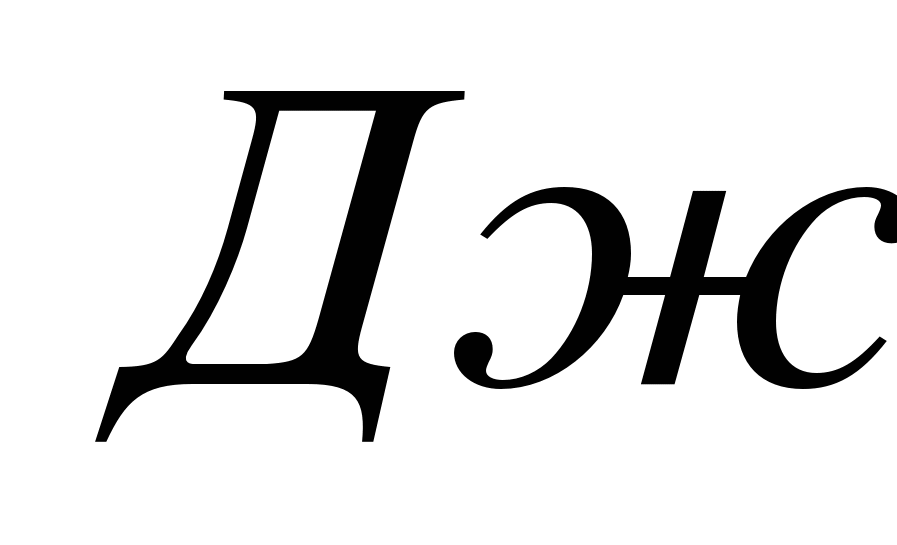 .
.
 определяют при средней температуре стенки
определяют при средней температуре стенки 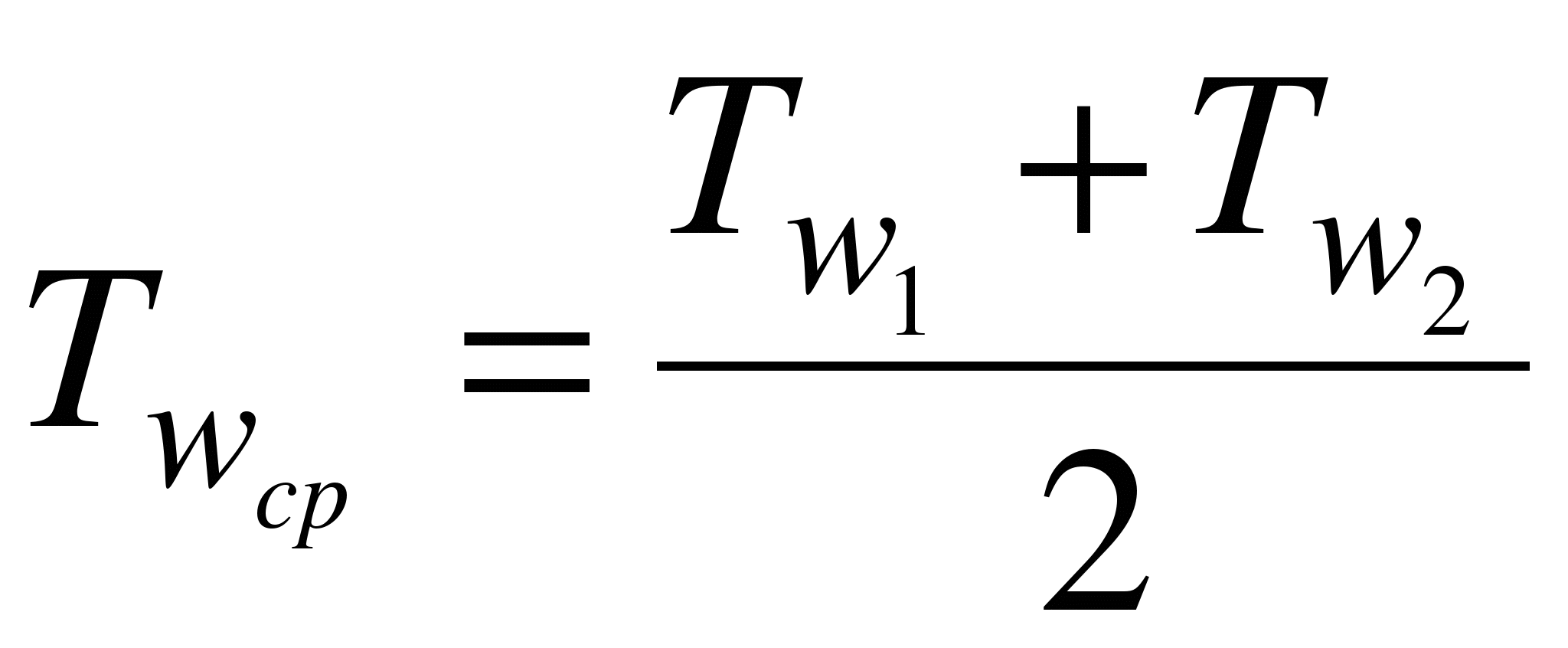 .
.
Плотность теплового потока:
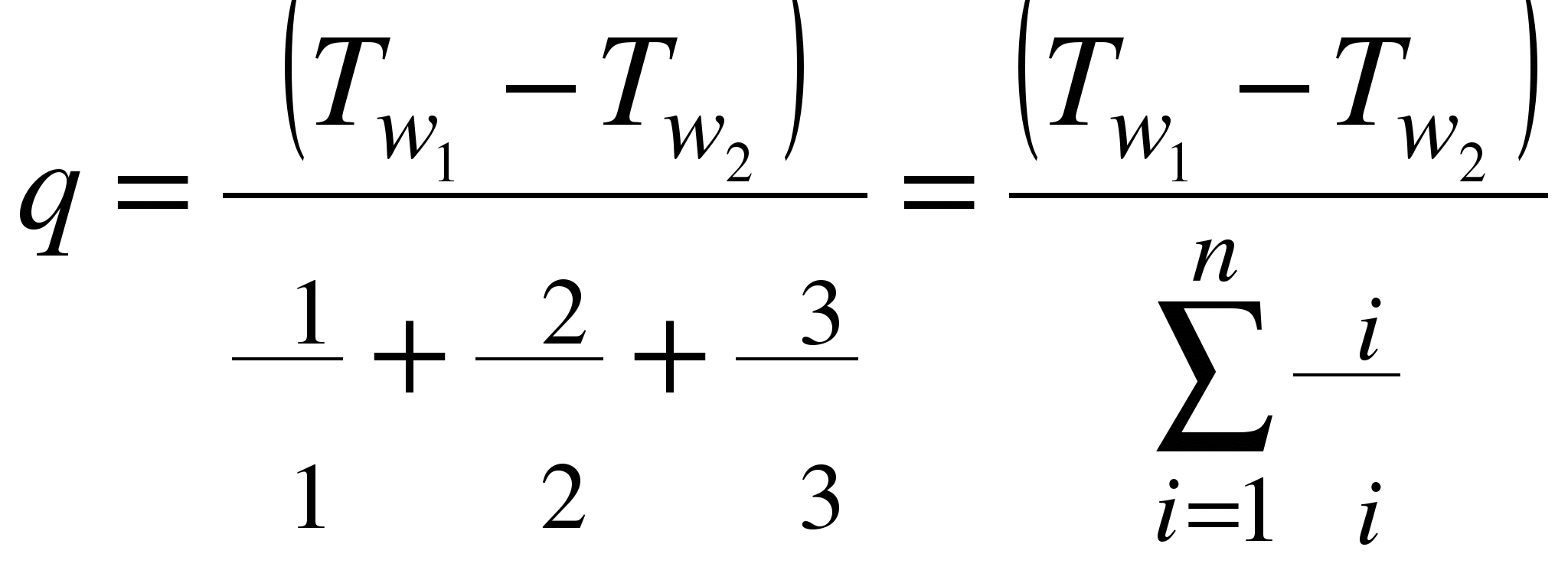 ,
,
где 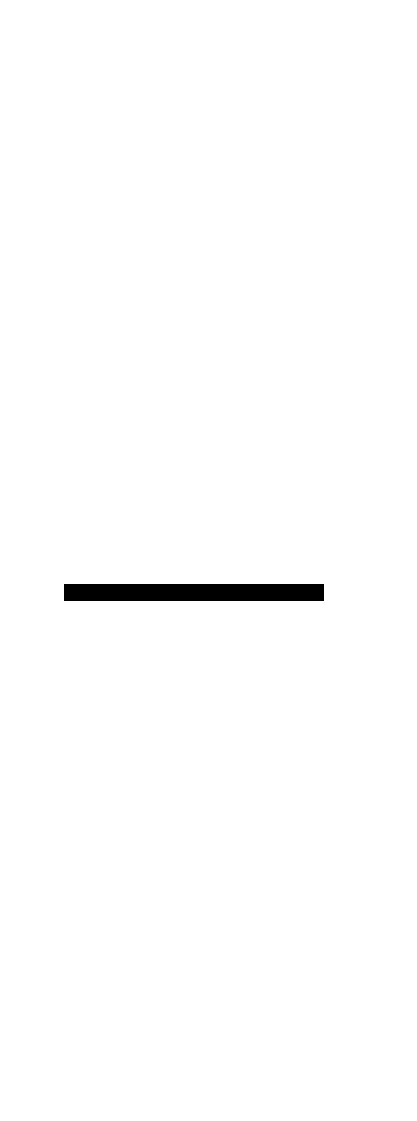 - термическое сопротивление слоя;
- термическое сопротивление слоя; 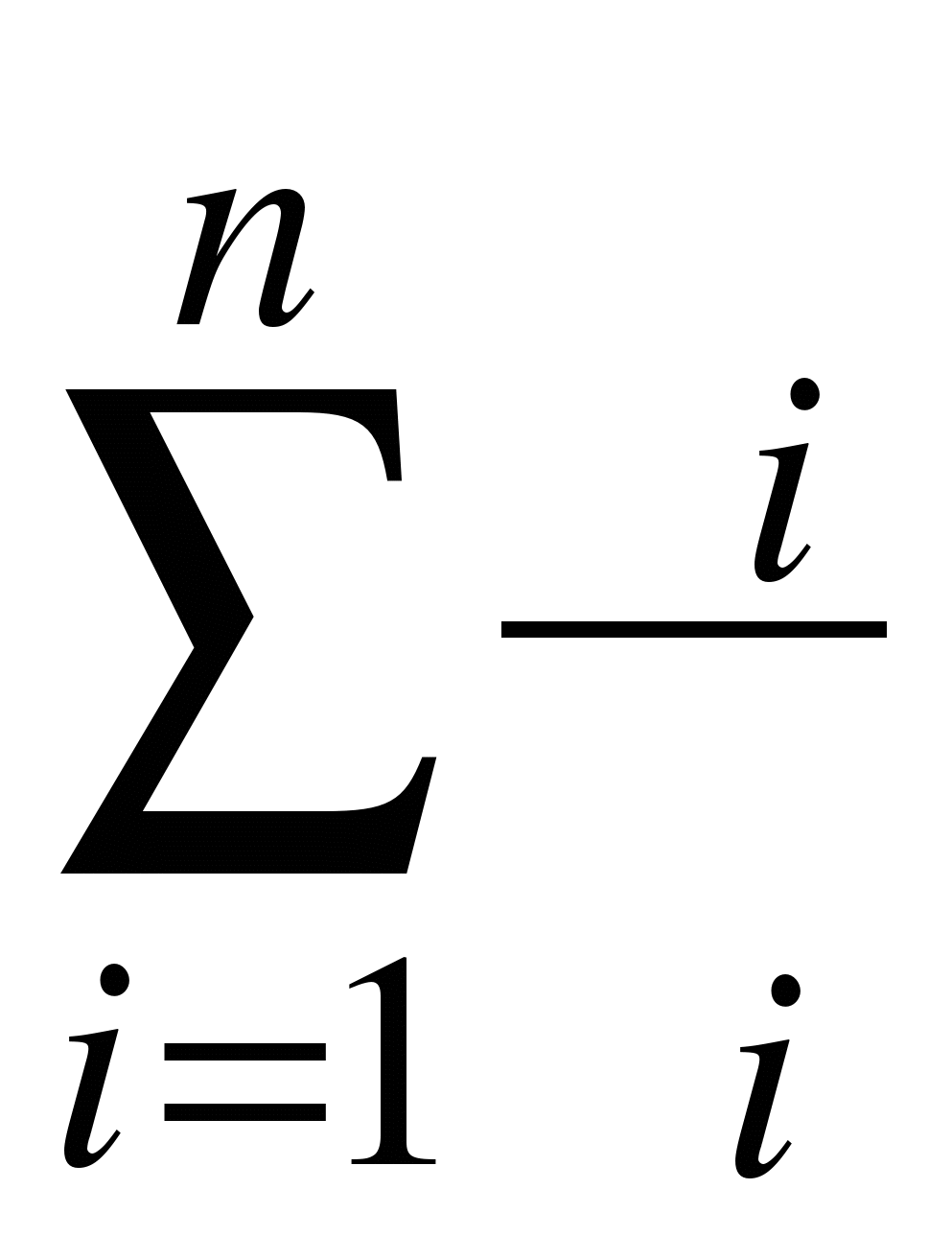 - полное термическое сопротивление плоской многослойной стенки.
- полное термическое сопротивление плоской многослойной стенки.
Температуры между отдельными слоями многослойной стенки:
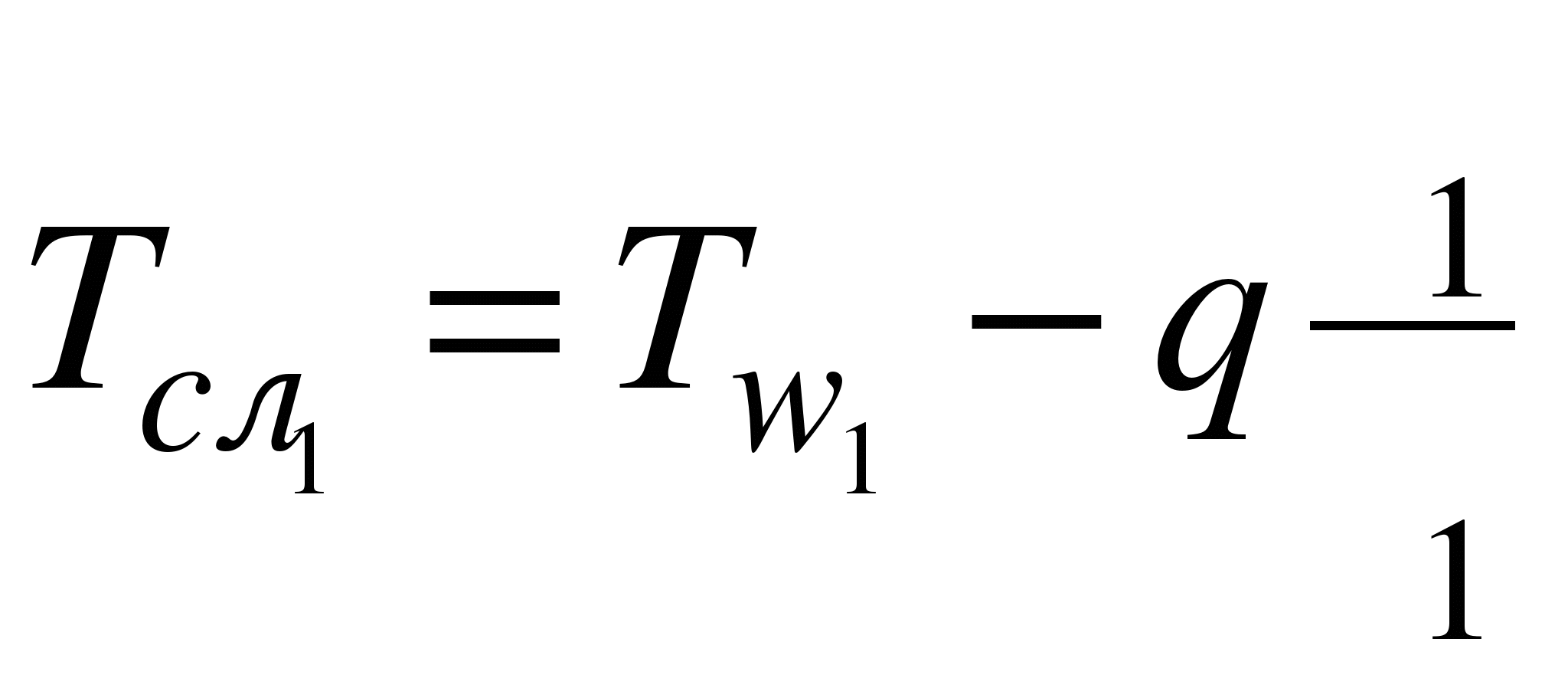 ;
;
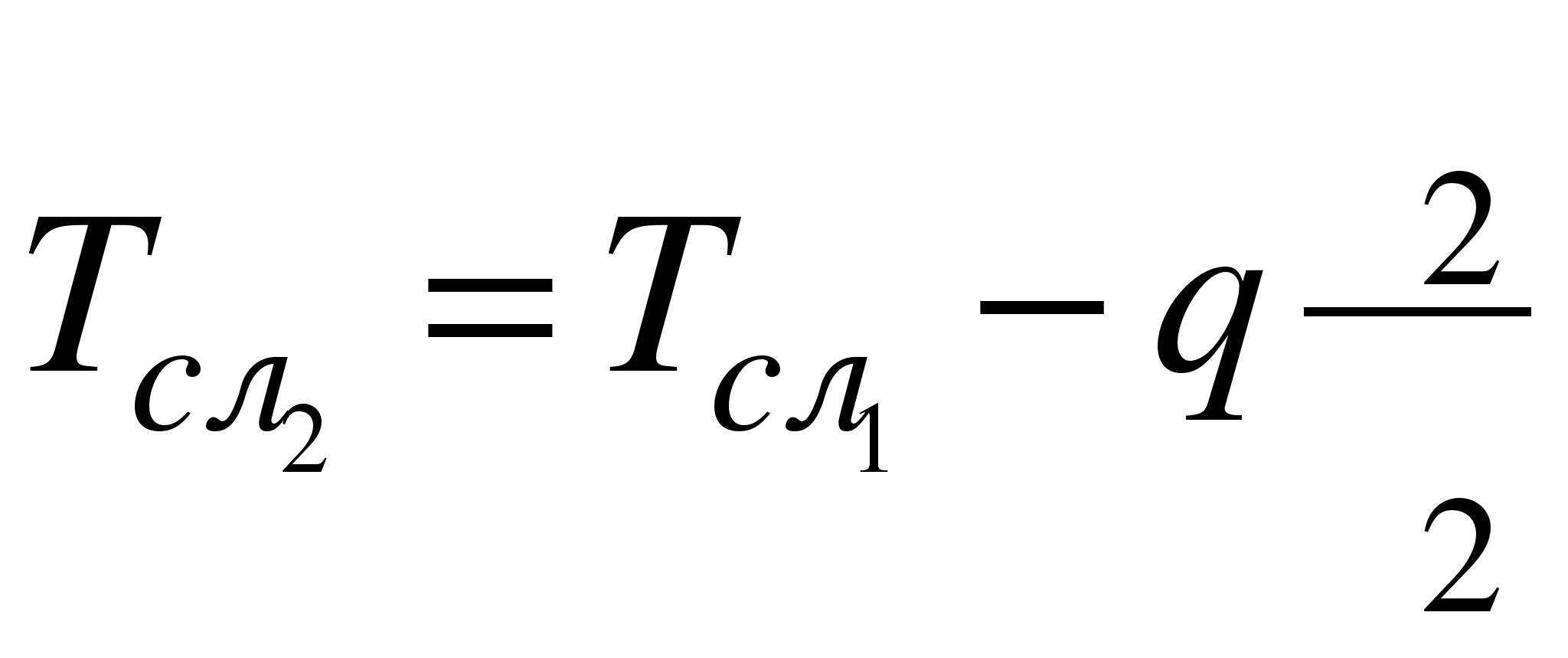 ;
;

и т.д.
4 Теплоптоводность ч/з цил-ую стенку.

На границах стенки заданы ГУ 1-го рода.
при r=r1, t=tw1
при r=r2 , t=tw2
в этом случае тепловой поток имеет радиальное направление, темпер. поле одномерно. для стационар. одномер. задачи о теплопро-ти цил. стенки дифур-ие (1.5) в цил-й системе коорд-т при λ=const примет
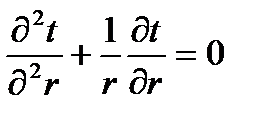 (1.14)
(1.14)
введя новую переменную г=  , преобр-ем (1.14)
, преобр-ем (1.14)

после раздел-я перем-х и интегр-я получим lnu + lnr = lnC1 (1.15)
потенцируя получим u*r= C1
перейдя к первонач переем-м, запишем  r
r  = C1, а затем разделив получаем
= C1, а затем разделив получаем
t= C1lnr+ C2 (1.16)
искривление линии темпер-го поля в цил-ой стенке обуслов-о изменением плотности тепл-го потока q=  при изменении радиуса цилиндра. при увеличении r величина площади F=2πrl, где l – длина стенки, также увел-ся. поэтому на больших r темп-ая линия проходит более полого и наоборот. Это правило сохр-ся и при обратном направ-ии тепл. потока(пунктир на рис.).
при изменении радиуса цилиндра. при увеличении r величина площади F=2πrl, где l – длина стенки, также увел-ся. поэтому на больших r темп-ая линия проходит более полого и наоборот. Это правило сохр-ся и при обратном направ-ии тепл. потока(пунктир на рис.).
Подставив ГУ в (1.16) найдем C1 и C2:
C1= 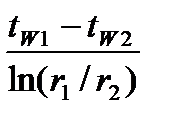 C2 =
C2 = 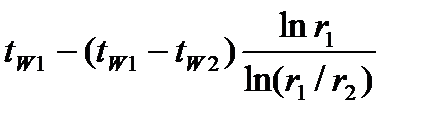 (1.18)
(1.18)
преобр-м 1.16 с учетом 1.18:  (1.19)
(1.19)
где d1 и d2 – внутр и наруж диам-ы цилиндра, d – текущ-й диам-р цил-ра.
из (1.19) опред-им темпер-й градиент:  =
= 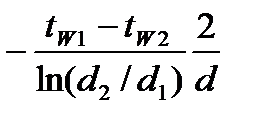 (1.20)
(1.20)
использ (1.20) найдем тепл-й поток ч/з стенку: Q=qF=-λ  2πrl=
2πrl= 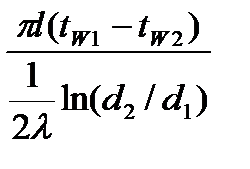 (1.21)
(1.21)
тепловой поток на единицу длины 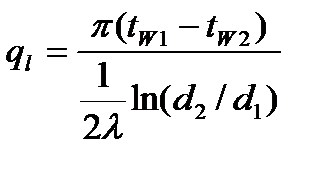 (1.22)
(1.22)
величину 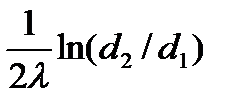 назыв внутр термич сопр-ем цил стенки.обозначим плотности тепл. потока на внутр и внеш поверх-ях ч/з
назыв внутр термич сопр-ем цил стенки.обозначим плотности тепл. потока на внутр и внеш поверх-ях ч/з 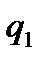 и
и  . т.к. Q=
. т.к. Q= 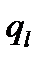 l=
l=  π
π 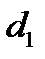 l=
l= 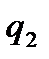 π
π 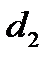 l
l
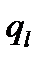 =
=  π
π 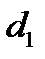 =
=  π
π 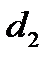 (1.23)
(1.23)
5 Теплопередача ч/з цилиндр
Принцип расчета теплового потока через цилиндрическую стенку аналогична как и для плоской стенки. Рассмотрим однородную трубу (рис.12.2) степлопроводностью l, внутренний диаметр d1, наружный диаметр d2, длина l. Внутри трубы находится горячая среда с температурой t'ж, а снаружи холодная среда с температурой tж
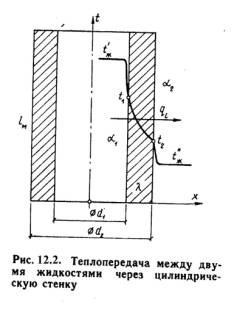
оличество теплоты, переданной от горячей среды к внутренней стенке трубы по закону Ньютона-Рихмана имеет вид:
Q = p·d1·a1·l·(t'ж – t1), (12.9)
где a1 – коэффициент теплоотдачи от горячей среды с температурой t'ж к поверхности стенки• с температурой t1;
Тепловой поток, переданный через стенку трубы определяется по уравнению:
Q = 2·p·l·l·(t1 – t2) / ln (d2/d1). (12.10)
Тепловой поток от второй поверхности стенки трубы к холодной среде определяется по формуле:
Q = p·d2·a2·l·(t1 - t''ж), (12.11)
где a2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t''ж.
Решая эти три уравнения получаем:
Q = p l·(t'ж – t''ж) • К, (12.12)
где Кl = 1/[1/(a1d1)+ 1/(2lln(d2/d1) + 1/(a2d2)] – (12.13)
- линейный коэффициент теплопередачи,
или Rl = 1/ Кl = [1/(a1d1)+ 1/(2lln(d2/d1) + 1/(a2d2)] – (12.14)
· полное линейное термическое сопротивление
теплопередачи через однослойную цилиндрическую стенку.
1/(a1d1), 1/(a2d2) – термические сопротивления теплоотдачи поверхностей стенки;
1/(2lln(d2/d1) - термическое сопротивление стенки.
Для многослойной (n слоев) цилиндрической стенки полное линейное термическое сопротивление будет определяться по следующей формуле:
Rl = 1/ Кl = [1/(a1d1)+ 1/(2l1ln(d2/d1) + 1/(2l3ln(d3/d2) + …
+ 1/(2lnln(dn+1/dn) + 1/(a2dn)] – (12.15)
При выводе формул для многослойной стенки предполагалось, что слои плотно прилегают друг к другу, и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. Идеально плотный контакт между отдельными слоями многослойной стенки получается, если одни из слоев наносят на другой слой в жидком состоянии или в виде текучего раствора. Твердые тела касаются друг друга только вершинами профилей шероховатостей (рис.4). Площадь контакта вершин пренебрежимо мала, и весь тепловой поток идет через воздушный зазор (h). Это создает дополнительное (контактное) термическое сопротивление Rк. Термические контактные сопротивления, могут быть определены самостоятельно с использованием соответствующих эмпирических зависимостей или экспериментально. Например, термическое сопротивление зазора в 0,03 мм примерно эквивалентно термическому сопротивлению слоя стали толщиной около 30 мм.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 1507; Нарушение авторских прав?; Мы поможем в написании вашей работы!