Особенности механических свойств биотканей

Переходя к рассмотрению механических свойств именно биологических тканей, заранее выделим присущие большинству из них общие черты в механическом поведении.

1. Большинство биологических тканей анизотропно, т.е. их физические, в том числе и механические свойства в различных направлениях неодинаковы. Анизотропия биотканей связана, прежде всего, с определенным порядком в расположении строящих ее структурных элементов.

2.Почти все биоткани обнаруживают при деформировании характерные временные эффекты:

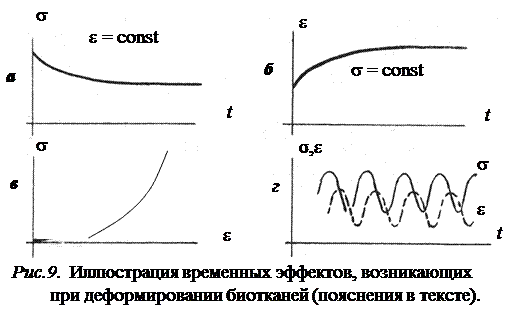
а) при фиксированной величине деформации в биотканях со временем происходит релаксация (спад) механического напряжения (рис. 9 а);

б) при фиксированной нагрузке (механическом напряжении) со временем растëт величина деформации (рис. 9 б) – это явление обычно называют ползучестью (или крипом);

в) при циклическом нагружении биотканей в них возникают колебания механических напряжений и деформаций, которые отличаются по фазе, причëм деформация отстает по фазе от механического напряжения (рис. 9 г);

г) механические характеристики биотканей часто зависят от скорости деформации.

3. Зависимостям механического напряжения от деформации при нагрузке и разгрузке соответствуют разные кривые. В результате образуется так называемая петля гистерезиса (рис. 9 в).

Перечисленные в пунктах 2 и 3 факты – проявление вязкоупругого поведения биоткани.

Остановимся на содержании понятия «вязкоупругость» несколько подробнее. Внешние силы, действующие на образец, выполненный из некоторого материала, совершают работу по его деформированию. Энергия, затраченная на деформацию образца, может во-первых запасаться в объеме деформированной среды в виде потенциальной энергии деформации и во-вторых, она может необратимо расходоваться на преодоление сил внутреннего трения, переходя в конечном итоге в теплоту.

Если при деформации реализуется только первый случай, то материал, из которого изготовлен образец, является упругой средой, и при разгрузке образца вся запасенная в нем потенциальная энергия деформации переходит в работу по восстановлению его прежних размеров и формы.

Если реализуется только вторая возможность, т.е. происходит лишь необратимое рассеивание энергии в образце, то среда называется вязкой. Все деформации в такой среде необратимы (неупруги).

Если же в разной степени реализуется и первая и вторая возможность, то среда называется вязкоупругой. При еë деформировании часть работы внешних сил запасается в образце в виде энергии упругой деформации, а оставшаяся часть необратимо рассеивается в виде тепла. В зависимости от степени проявления этих возможностей после прекращения действия внешних сил происходит большее или меньшее частичное восстановление размеров и формы образца. Так формируется петля гистерезиса (рис. 9, в), причем площадь между кривыми нагрузки и разгрузки образца определяет долю необратимо затраченной энергии, перешедшей в тепло.

Таков общий подход к описанию механических свойств реальных, в том числе и биологических сред, который используется в биомеханике для объяснения механического поведения биотканей.

Одна из главных задач механики деформируемых сред – установление связей между механическими напряжениями, деформациями и скоростями деформации. Рассмотрим несколько примеров таких связей:

а) идеально упругое изотропное тело Гука. В этом случае связь между механическим напряжением и деформацией тела определяется законом Гука:

· для одноосного растяжения или сжатия (рис. 6 б, в) s = Е × e,

· для деформации сдвига (рис. 6 д) t = G × g,

б) ньютоновская вязкая жидкость. В этом случае сила внутреннего трения, действующая по касательной к слоям текущей жидкости, определяется известной формулой Ньютона:

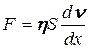. (9)

где h - коэффициент динамической вязкость, его размерность в СИ – Па×с, S – площадь соприкосновения слоев текущей жидкости, 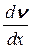– градиент скорости. Формулу (9) часто записывают в другом виде:

t = h 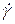. (10)

Здесь t*= 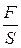– механическое напряжение сдвига, возникающее в текущей жидкости, 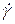– скорость сдвига, причем 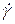= . Эквивалентность формул (9)и (10) подтверждает следующий простой анализ. 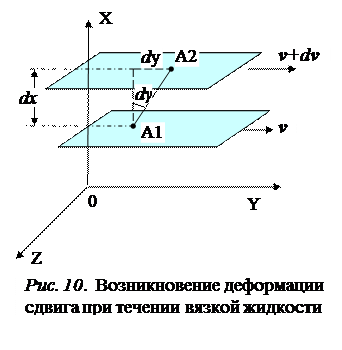Выделим две частицы жидкости А1 и А2 в двух слоях, текущих параллельно плоскости ZОY и перпендикулярно оси ОХ (Рис.10). Расстояние между слоями dx, а относительная скорость их течения равна d v. Поэтому за время dt частица А2 верхнего слоя пройдет вдоль ОY путь больший на d y, чем частица А1 нижнего слоя: d y = d v ∙dt. В результате в текущей жидкости возникает деформация сдвига, мерой которой является угол сдвига d γ = 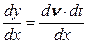. Отсюда следует равенство между скоростью сдвига и градиентом скорости –

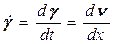и переход от (9) к (10).

в) рассмотрим одну из возможных комбинаций упругости и вязкости – простейшее вязкоупругое твердое тело (тело Кельвина-Фойгта), которое позволяет провести приближенный анализ явления ползучести. При суммировании напряжения сдвига упругого тела Гука и ньютоновской вязкой жидкости получим следующее уравнение для касательного напряжения в этом теле:

t = G g + h 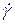, или 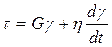, (t – время). (11)

Пусть в теле, которому соответствует дифференциальное уравнение (11), в начальный момент времени t = 0 возникает напряжение t = t₀, которое затем поддерживается постоянным. Тогда решение дифференциального уравнения (11), имеет вид:

, (12)

где параметр l = h/ G имеет размерность времени и называется временем запаздывания. Он зависит только от свойств материала деформируемого образца (h и G) и характеризует запаздывание реакции материала (величины его деформации) на приложенную нагрузку. Следовательно, развитие упругой деформации в такой среде тормозится вязкостью этой среды.

После снятия внешней нагрузки будет происходить упругое восстановление тела, которое описывается формулой:

(13)

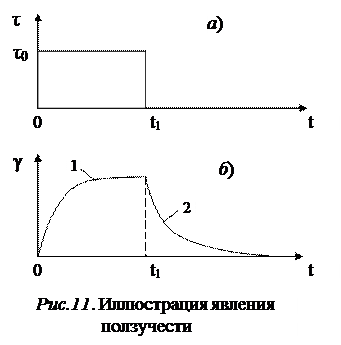
На рис. 11, а приведен график нагружения образца: зависимость прилагаемого к образцу механического напряжения от времени, а на рис.11, б – зависимость величины его деформации γ от времени t. Она представлена кривой ползучести 1 при мгновенном нагружении образца и кривой 2, соответствующей последующему восстановлению образца после мгновенного разгружения.

Кроме того, установлено, что реакция (отклик) такой среды на внешнее воздействие зависит и от скорости ее деформирования, т.е. от величины .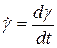

При циклическом нагружении образца возникает разность фаз (запаздывание) между напряжением и деформацией, которая растет с увеличением частоты внешнего воздействия и времени запаздывания.

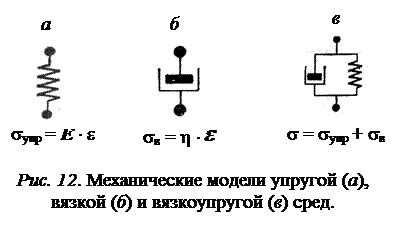При анализе механического поведения той или иной среды, в том числе и при решении многих прикладных задач в биомеханике, используются наглядные механические модели (рис.12).

Например, пружина моделирует идеальную упругость (рис.12, а); проницаемый (т.е. с отверстиями для выхода жидкости) поршень в цилиндре с маслом – вязкость (рис. 12, б), а их разные сочетания соответствуют более сложным случаям вязкоупругих сред.

В частности, уже рассмотренное тело Кельвина–Фойгта при таком подходе может быть представлено как параллельное соединение пружины и проницаемого поршня (рис.12, в)*. При мгновенном приложении силы начальная деформация модели будет равна нулю, так как вязкий элемент (проницаемый поршень в вязкой среде) не даст возможности ей развиться. Затем произойдет постепенное перемещение поршня в вязком элементе, а вместе с этим сможет растягиваться и пружина. Деформация будет постепенно нарастать, и, если напряжение постоянно, зависимость еë от времени опишется формулой (12) и кривой 1 на рис. 11, б. Снимая нагрузку мы дадим возможность растянутой пружине сокращаться, но вязкий элемент не позволит это сделать мгновенно. Сокращение пройдет быстро в первые моменты времени, когда возвращающая сила пружины сравнительно велика. Затем возвращение системы в исходное состояние замедлится и в конце концов деформация исчезнет полностью (кривая 2 на рис. 11, б).

Комбинируя вязкие и упругие элементы, добавляя к ним элементы, отображающие сухое трение, инерционность, силу взаимодействия двух соседних элементов среды и др., можно получить модели сред с весьма сложными механическими свойствами.

Дата добавления: 2015-05-09