Уравнения Хилла

Примеры режимов сокращения

Изометрический режим	Изотонический режим
Жевательные мышцы при сомкнутых челюстях (огромное напряжение)	Сокращение бицепса плеча
Сокращение миокарда желудочков при закрытых клапанах	Сокращение миокарда желудочков при открытии полулунных клапанов

Между нагрузкой (Р) и скоростью укорочения мышцы (v) при изотоническом сокращении существует зависимость, выражаемая уравнением Хилла:

или

где а — постоянная, имеющая размерность силы; Р_о — постоянная, соответствующая максимальной силе, развиваемой в изотоническом режиме (максимальный груз, который удерживает мышца без ее удлинения); b — константа, имеющая размерность скорости.

Анализ уравнения (11.7) показывает, что в зависимости от нагрузки Р поведение мышцы, т. е. ее сокращение, проявляется по-разному. Рассмотрим два крайних случая.

Нагрузка	Скорость	Поведение мышцы
P=0		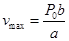Максимальная скорость сокращения мышцы
P=P0	v =0	Сокращения мышцы не происходит

Рассмотрим энергетические характеристики процесса. Работа А, совершаемая мышцей при одиночном укорочении на величину ∆ l, определяется известной формулой:

А = Р∙ ∆ l.

Эта зависимость очевидно нелинейная, так как скорость сокращения мышцы (v) зависит от нагрузки (Р). Но на ранней стадии сокращения этой нелинейностью можно пренебречь и считать v = const. Тогда

∆ l = v ∙∆ t,

аразвиваемая мышцей мощность имеет вид:

W=P∙v. (11.8)

Подставляя (11.7) в (11.8), получим зависимость полной мощности от развиваемой силы Р:

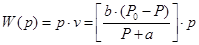(11.9)

График функции (11.9) имеет колоколообразную форму и представлен на рис. 11.22 в относительном виде.

Рис. 11.22. Зависимость мощности мышцы от нагрузки

Эта кривая, полученная из уравнения Хилла, хорошо согласуется с опытными данными. В зависимости от нагрузки Р мощность имеет разные значения

Мощность	Нагрузка
W=0	Р=Р0
W=0	P=0
W — максимальна	, когда P=0,31P0

При работе мышц КПД при сокращении может быть определен как отношение совершенной работы к затраченной энергии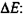

Развитие наибольшей мощности и эффективности сокращения достигается при усилиях 0,3—0,4 от максимальной изометрической нагрузки Р₀ для данной мышцы. Это используют, например, спортсмены-велогонщики: при переходе с равнины на горный участок нагрузка на мышцы возрастает и спортсмен переключает скорость на низшую передачу, тем самым уменьшая Р, приближая ее к Р_опт.

Практически КПД может достигать 40—60% для разных типов мышц.

Среднее значение плотности мышечной ткани 1050 кг/м³. Модуль Юнга Е =10⁵ Па.

Дата добавления: 2015-05-09