Дисконтування анюїтетів (ренти)

Приклад 2.

Підприємцю запропонували вибір:

І варіант- трьохрічна рента з виплатою 100 гр.од. в кінці кожного року;

ІІ варіант-трьохрічна рента з виплатою 100 гр.од. на початку кожного року;

ІІІ варіант- одноразова виплата всієї суми 300 гр.од. по закінченні 3 років.

Процентна ставка - 5% в усіх випадках.

Варіант І.

Визначимо поточну вартість кожного потоку грошей, потім підсумовуємо ці показники і одержуемо PV ренти.

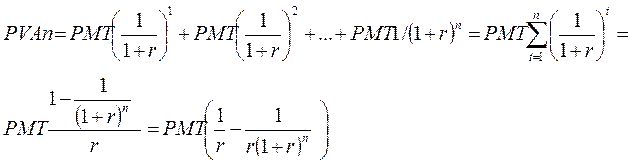Рівняння для визначення теперішньої вартості анюїтетів (ренти):

Отже,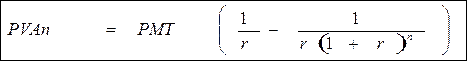

Якщо винести за дужку відсоткову ставку, то формула набуде такого вигляду:

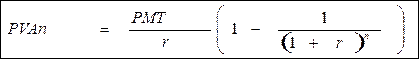
Різниця в дужках рівняння) називається фактором відсотку поточної вартості ренти (PVIFAr,n). В таблиці визначення теперішньої вартості анюїтетів обчислено значення цього показника для різних n та r. Рівняння матиме вигляд:

PVA_n=PMT(PVIFAr_,n)

Фактор відсотку поточної вартості ренти (PVIFAr,n) - це показник анюїтетів за n -ну кількість періодів, дисконтований на r відсотків. PVIFA _5%,3 =2,7232

PVA₃ = 100 гр.од. х (PVIFA _5%,3) = 100 гр.од. х 2,7232 = =272,32 гр.од.

Варіант ІІ.

При вексельній ренті кожний платіж буде зміщений вліво на 1 рік, тобто, буде дисконтуватись на 1 рік менше.

Принцип же вирахування такий самий, як і при звичайному анюїтеті. Оскільки виплати виконуються швидше, вексельна рента має більшу вартість, ніж звичайна. Рівняння для вексельної ренти

PVA (вексельна) = РМТ х (PVIFAr,n) х (1+ r)

PVA (вексельна) = 100 гр.од. х 2,7232 х 1,05 = 285,94гр.од.

Варіант ІІІ.

За допомогою рівняння теперішньої вартості грошей і таблиці отримаємо:

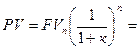FVn x PVIF _5%,3 = 300 x 0,8638 = 259,14 гр.од.

Наведені підрахунки показують, що три надходження по 100 гр.од. кожного року протягом 3 років тепер коштують лише 272,32 гр.од. за дисконта 5% при звичайній ренті або 285,94 гр.од. за цієї ж ставки відсотку при вексельній. Ці приклади демонструють суть дисконтування. Різниці між сумами

300 гр.од. - 272,32 гр.од. = 27,68 гр.од.

300 гр.од. - 285,94 гр.од. = 14,06 гр.од.

є різницями вартості грошей з часом, або загальний дисконт.

При одноразовому вкладанні 300 гр.од. на 3 роки зиск становить

300 - 259,14 = 40,86 гр.од.

Тобто прибуток від вкладання одноразово набагато більший, але і ризик з часом зростає, адже ці гроші “лежать” на депозитному рахунку всі 3 роки. Цей приклад ще раз підтверджує концепцію, що чим вище ризик, тим більша компенсація за цей ризик, і сьогодні гроші дорожчі, ніж завтра.

Таким чином, підприємство обере той варіант вкладання грошей, який, на його думку, буде не тільки більш привабливим з точки зору розрахунків, а буде також враховувати суб’єктивні фактори: загальну ризикованість операції; репутацію банку, що відкриває депозитний рахунок; можливості швидкого та ефективного реінвестування отриманих грошей, тощо.

Дата добавления: 2015-05-07