Реальные газы. Критическое состояние вещества. Фазовые равновесия и фазовые превращения. Понятие фазы и фазового равновесия

Необратимость тепловых процессов. Термодинамическая вероятность и энтропия. Энтропия изолированной системы. Неравенство Клаузиуса. Третье начало термодинамики (теорема Нернста) и следствия из него.

Обратимые и необратимые процессы. Второе начало термодинамики и его статистическое толкование. Необратимость тепловых процессов. Преобразование энергии в тепловых двигателях. Принцип работы тепловых двигателей и холодильных машин. Цикл Карно и его коэффициент полезного действия.

Первый закон (первое начало) термодинамики (закон сохранения энергии в тепловых процессах). Применение первого начала термодинамики к изопроцессам в газах. Адиабатический процесс. Уравнение Пуассона. Политропный процесс.

Теплоемкость. Зависимость теплоемкости идеального газа от степени свободы молекул и от вида процесса теплопередачи (изохорного, изобарного, изотермического, адиабатного). Уравнение Майера.

Степени свободы молекул газа. Закон равномерного распределения энергии теплового движения молекул газа по степеням свободы (теорема Больцмана). Внутренняя энергия идеального газа.

Число степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве.

В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью. Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных.

В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы

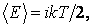
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i = i _пост+ i _вращ+2 i _колеб
Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий N_A молекул:

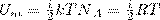
Внутренняя энергия для произвольной массы m газа.

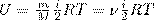
Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT:

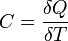
Молярная теплоемкость —величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:

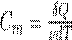
где ν =m/М—количество вещества.

Единица молярной теплоемкости — джоуль на моль•кельвин (Дж/(моль•К)).

Удельная теплоемкость с связана с молярной теплоемкостью С_m, соотношением

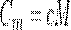
где М — молярная масса вещества.

Выделяют теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.
Если газ нагревается при постоянном объеме, то dV=0 и работа внешних сил равна также равна нулю. Тогда газу сообщаемая извне теплота идет только на увеличение его внутренней энергии:

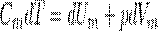
т. е. молярная теплоемкость газа при постоянном объеме С_V равна изменению внутренней энергии одного моль газа при повышении его температуры на 1 К. Поскольку U_m=(i /2)RT, то

Если газ нагревается при постоянном давлении, то выражение можно представить в виде

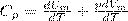
Учитывая, что (U_m/dT) не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна С_V), получаем

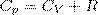(1)

Выражение (1) называется уравнением Майера; оно говорит о том, что С_p всегда больше С_V ровно на величину молярной газовой постоянной. Это объясняется тем, чтобы осуществить нагревание газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.

При исследовании термодинамических процессов важно знать характерное для каждого газа отношение С_p к С_V:

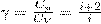
Молярные теплоемкости зависят лишь от числа степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, которое проявляется в теплоемкости, зависит от температуры.

13. Затруднения и недостатки классической теории теплоемкости идеальных газов. Закон Дюлонга – Пти.

Однако, в целом классическая теория теплоемкости газов не может считаться вполне удовлетворительной. Существует много примеров значительных расхождений между теорией и экспериментом. Это объясняется тем, что классическая теория не в состоянии полностью учесть энергию, связанную с внутренними движениями в молекуле.

Теорему о равномерном распределении энергии по степеням свободы можно применить и к тепловому движению частиц в твердом теле. Атомы, входящие в состав кристаллической решетки, совершают колебания около положений равновесия. Энергия этих колебаний и представляет собой внутреннюю энергию твердого тела. Каждый атом в кристаллической решетке может колебаться в трех взаимно перпендикулярных направлениях. Следовательно, каждый атом имеет 3 колебательные степени свободы. При гармонических колебаниях средняя кинетическая энергия равна средней потенциальной энергии. Поэтому в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. Внутренняя энергия 1 моля твердого вещества равна:

U = 3N_АkT = 3RT.

Поэтому молярная теплоемкость вещества в твердом состоянии равна:

C = 3R = 25,12 Дж/моль·К.

Это соотношение называется законом Дюлонга–Пти. Для твердых тел практически не существует различия между C_p и C_V из-за ничтожно малой работы при расширении или сжатии.

Опыт показывает, что у многих твердых тел (химических элементов) молярная теплоемкость при обычных температурах действительно близка к 3R. Однако, при низких температурах наблюдаются значительные расхождения между теорией и экспериментом. Это показывает, что гипотеза о равномерном распределении энергии по степеням свободы является приближением. Наблюдаемая на опыте зависимость теплоемкости от температуры может быть объяснена только на основе квантовых представлений.

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии длятермодинамических систем.

Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.

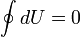
δ Q = δ A + dU, где dU есть полный дифференциал внутренней энергии системы, а δ Q и δ A есть элементарное количество теплоты, переданное системе, и элементарная работа, совершенная системой соответственно.

Первое начало термодинамики:

§ при изобарном процессе

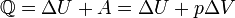
§ при изохорном процессе (A = 0)

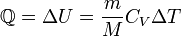
§ при изотермическом процессе (Δ U = 0)

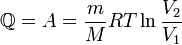
Здесь 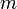— масса газа, 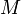— молярная масса газа, 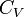— молярная теплоёмкость при постоянном объёме, 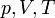— давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёттепловой энергии

Для идеальных газов адиабата имеет простейший вид и определяется уравнением:

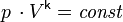
где:

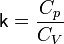§ — показатель адиабаты,

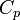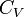§ и — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду:

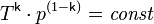, где T — абсолютная температура газа.

Или к виду:

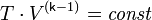
Поскольку 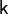всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов.

Политропный процесс — термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.

Для идеального газа уравнение политропы может быть записано в виде:

pVⁿ = const

где величина 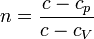называется показателем политропы.

В зависимости от процесса можно определить значение n:

1. Изотермический процесс: n = 1, так как PV ¹ = const, значит PV = const, значит T = const.

2. Изобарный процесс: n = 0, так как PV ⁰ = P = const.

3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона.

Здесь γ — показатель адиабаты.

4. Изохорный процесс: 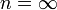, так как 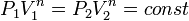, значит P ₁ / P ₂ = (V ₂ / V ₁) ⁿ, значит V ₂ / V ₁ = (P ₁ / P ₂)^{(1 / n )}, значит, чтобы V ₂ / V ₁ обратились в 1, n должна быть бесконечность.

Процесс называют обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходное через ту же последовательность промежуточных состояний, что и в прямом процессе, но проходимую в обратном порядке. При этом в исходное состояние возвращается не только система, но и среда. Обратимый процесс возможен, если и в системе, и в окружающей среде он протекает равновесно. При этом предполагается, что равновесие существует между отдельными частями рассматриваемой системы и на границе с окружающей средой. Обратимый процесс - идеализированный случай, достижимый лишь при бесконечно медленном изменении термодинамических параметров. Скорость установления равновесия должна быть больше, чем скорость рассматриваемого процесса. Если невозможно найти способ вернуть и систему, и тела в окружающей среде в исходное состояние, процесс изменения состояния системы называют необратимым.

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действияне может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Процессы, в ходе которых система все время остается в состоянии равновесия, называются квазистатическими. Все квазистатические процессы обратимы. Все обратимые процессы являются квазистатическими. Если рабочее тело тепловой машины приводится в контакт с тепловым резервуаром, температура которого в процессе теплообмена остается неизменной, то единственным обратимым процессом будет изотермический квазистатический процесс, протекающий при бесконечно малой разнице температур рабочего тела и резервуара. При наличии двух тепловых резервуаров с разными температурами обратимым путем можно провести процессы на двух изотермических участках. Поскольку адиабатический процесс также можно проводить в обоих направлениях (адиабатическое сжатие и адиабатическое расширение), то круговой процесс, состоящий из двух изотерм и двух адиабат (цикл Карно) является единственным обратимым круговым процессом, при котором рабочее тело приводится в тепловой контакт только с двумя тепловыми резервуарами.Все остальные круговые процессы, проводимые с двумя тепловыми резервуарами, необратимы.

Теплово́й дви́гатель — устройство, совершающее работу за счет использования внутренней энергии топлива, тепловая машина, превращающая тепло в механическую энергию использует зависимость теплового расширения вещества от температуры. Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем и охладителем.

Работа, совершаемая двигателем, равна:

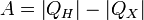, где:

§ Q_H — количество теплоты, полученное от нагревателя,

§ Q_X — количество теплоты, отданное охладителю.

Коэффициент полезного действия (КПД) теплового двигателя рассчитывается как отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя: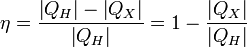

Часть теплоты при передаче неизбежно теряется, поэтому КПД двигателя менее 1. Максимально возможным КПД обладает двигатель Карно. КПД двигателя Карно зависит только от абсолютных температур нагревателя(T_H) и холодильника(T_X):

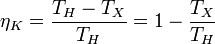
Пусть тепловая машина состоит из нагревателя с температурой T_H, холодильника с температурой T_X и рабочего тела.

Цикл Карно состоит из четырёх стадий:

1. Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру T_H, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Q_H. При этом объём рабочего тела увеличивается.

2. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

3. Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру T_X, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Q_X.

4. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия (поскольку 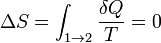при δ Q = 0).

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

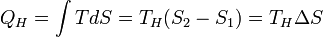Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

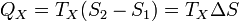Отсюда коэффициент полезного действия тепловой машины Карно равен

.

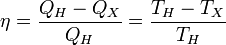Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми.

Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние. По определению термодинамическая вероятность W >> 1. Например, если в сосуде находится 1 моль газа, то возможно огромное число N способов размещения молекулы по двум половинкам сосуда: 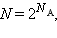где 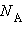– число Авогадро. Каждый из них является микросостоянием. Только одно из микросостояний соответствует случаю, когда все молекулы соберутся в одной половинке (например, правой) сосуда. Вероятность такого события практически равна нулю. Наибольшее число микросостояний соответствует равновесному состоянию, при котором молекулы равномерно распределены по всему объему. Поэтому равновесное состояние является наиболее вероятным. Равновесное состояние с другой стороны является состоянием наибольшего беспорядка в термодинамической системе и состоянием с максимальной энтропией. Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом:

S = k ln W,

где k = 1,38·10–23 Дж/К – постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия.

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

§ «Энтропия изолированной системы не может уменьшаться».

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

КЛАУЗИУСА НЕРАВЕНСТВО -неравенство, выражающее теорему термодинамики: для кругового процесса

где 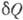- кол-во теплоты, сообщаемое системе (или отводимое от неё) на бесконечно малом участке цикла, Т _ абс. темп-pa соответствующего элемента среды. Кол-во теплоты 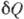, сообщаемое системе, считается положительным, отводимое от неё - отрицательным. Необратимому (хотя бы на одном участке) циклу соответствует неравенство, циклу, состоящему только из обратимых процессов,- знак равенства (равенство Клаузиуса). Величина 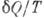наз. элементарной приведённой теплотой. К. н. даёт количеств. формулировку второго начала термодинамики.

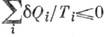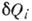К. н. установлено в 1850 Р. Клаузиусом с помощью Карно теоремы о максимальности кпд цикла Карно, т. к. любой круговой процесс можно рассматривать как предел большого числа элементарных циклов Карно и, следовательно, для него , где - кол-во теплоты, сообщаемое (отводимое) в i-м элементарном цикле Карно при темп-ре T_i.

Из равенства Клаузиуса следует, что 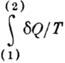не зависит от формы пути и 1 /T есть интегрирующий множитель для 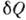. Это означает существование такой ф-ции состояния S, названной Клаузиусом энтропией, что 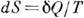. Для необратимого процесса из (*) следует, что

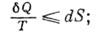
это неравенство также наз. К. н. Наряду с 1-м началом термодинамики К. н. может быть положено в основу построения термодинамики.

Третье начало термодинамики, тепловой закон Нернста (Нернста теорема), закон термодинамики, согласно которому энтропия S любой системы стремится к конечному для неё пределу, не зависящему от давления, плотности или фазы, при стремлении температуры (Т) к абсолютному нулю.

В 1911 М. Планк сформулировал Т. н. т. как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: .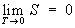

Из Т. н. т. следует, что абсолютного нуля температуры нельзя достигнуть ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться, поэтому Т. н. т. иногда формулируют как принцип недостижимости абсолютного нуля температуры.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

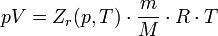
где p — давление; V - объем T — температура; Z_r = Z_r (p,T) — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная.

Критическое состояние вещества -

1) предельное состояние равновесия двухфазных систем, в котором обе сосуществующие фазы становятся тождественными по своим свойствам;

2) состояние вещества в точках фазовых переходов II рода. К. с., являющееся предельным случаем равновесия двухфазных систем, наблюдается в чистых веществах при равновесии жидкость — газ, а в растворах — при фазовых равновесиях газ — газ, жидкость — жидкость, жидкость — газ, твёрдое тело — твёрдое тело.

Фазовое равновесие, одновременное существование термодинамически равновесных фаз в многофазной системе. Простейшие примеры – равновесие жидкости со своим насыщенным паром, равновесие воды и льда при температуре плавления, расслоение смеси воды с триэтиламином на два несмешивающихся слоя (две фазы), отличающихся концентрациями.

Каждое вещество в зависимости от внешних условий - температуры и давления - может находиться в твердом, жидком и газообразном состоянии. При подводе или отводе теплоты меняется форма связи между молекулами, вызывая тем самым изменение вещества, т. е. происходит фазовое превращение. Для получения холода используют фазовые превращения, протекающие при низких температурах с поглощением теплоты из охлаждаемой среды. К ним относятся плавление, кипение и сублимация.

Плавление. Процесс перехода вещества из кристаллического состояния в жидкое с поглощением теплоты называют плавлением (например, при нагревании водного льда его температура повышается до температуры 0 ^оС, дальнейшее нагревание ведет к его плавлению).

Испарение. Процесс парообразования, происходящий со свободной поверхности жидкости при различных температурах, называют испарением.

Кипение. Процесс интенсивного парообразования, происходящий по всему объему жидкости в результате поглощения теплоты окружающей среды, называют кипением.

Сублимация. Процесс перехода тела из твердого состояния в парообразное, минуя промежуточное жидкое состояние, называют сублимацией.

Конденсация. Процесс превращения насыщенного пара в жидкость, сопровождающийся отводом выделяемой теплоты, называют конденсацией.

Термодинами́ческая фа́за — термодинамически однородная по составу и свойствам часть термодинамической системы, отделенная от других фаз поверхностями раздела, на которых скачком изменяются некоторые свойства системы. Другое определение: Фаза — гомогенная часть гетерогенной системы.

Дата добавления: 2015-05-09