Максимально возможная ошибка одного измерения

Необходимо выяснить, как будут влиять ошибки измерения отдельных величин на искомую величину определяемую при помощи формулы. Разбе­рем этот вопрос в общем виде.

Пусть искомая величина W является функцией нескольких (допус­тим, трех) величин, измеряемых непосредственно в опыте:

w=f(x,y,z)

(49)

Если бы ошибки в измерении величин x,y и z были бесконечно малыми, то ошибка в величине w, определялась бы ее полным дифференциалом:

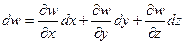
(50)

В действительности, ошибки в измерения величин x, y и z не будут бесконечно малыми, однако для расчета величины ошибки можно воспользоваться аналогичной формулой, подставляя вместо dx, dy и dz действительно конечные величины ошибок Δx, Δ y и Δ z.

Итак, получаем:

(51)

где Δw - максимально возможная абсолютная ошибка искомой вели­чины w;

Δx, Δy и Δ z - абсолютные ошибки в измерении величины x, y и z

По формуле (51) вычисляется максимально возможная ошибка, поэтому все ее члены берутся по абсолютному значению и суммируются.

В действительности, при проведении измерений ошибка может быть значительно меньше, так как входящие в (51) слагаемые могут иметь разные знаки, однако в наихудшем варианте все три слагаемые будут иметь один и тот же знак, что даст максимально возможную ошибку.

Часто требуется найти максимально возможную относительную ошибку δw=Δw/w. Её можно получить, разделив (51) на W, т.е.:

(52)

Формула (52) является общей, по ней можно вычислить максимально возможную ошибку искомой величины w при любой функциональной за­висимости w=f(x,y,z).

Для выражения δw в процентах формулу (52) следует умножить на 100.

В дополнение к общей формуле рассмотрим несколько частных случаев.

Очень часто встречается случай, когда искомая величина w определяется как произведение измеряемых величин x, y и z в различ­ных степенях и постоянной А, т.е.:

w=A·x^α · y^β · z^γ

(53)

Причем α, β и γ могут быть любыми положительными или отрица­тельными числами. Заметим, что формула (53) охватывает случаи, опи­санные формулами (49) и (50).

Для функциональной зависимости (40) можно получить более конкрет­ное выражение для подсчета максимально возможной относительной ошибки величины.

Возьмем производные, входящие в (52):

(54)

Подставив в (52) эти значения и значение w по (53), получим:

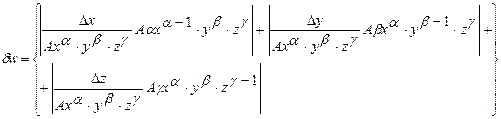
(55)

Откуда:

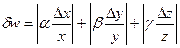
(56)

Обозначая относительные ошибки величин, непосредственно измеряемых в опыте:

(57)

Окончательно получаем:

δw=|αδx|+|βδy|+|γδz|

(58)

Эта формула еще больше упрощается, если α, β и γ равны единице или единице с минусом. Тогда получим:

δw=|δx|+|δy|+|δz|

(59)

Последнее можно сформулировать следующим образом: если искомая
величина w является произведением постоянной и измеряемых вели­чин x, y и z в первой или минус первой степени, то относительная ошибка искомой величины w является суммой относительных ошибок этих измеряемых величин.

Разберем другой случай. Пусть:

w = x + y + z

(60)

Определим величину максимально возможной относительной ошибки. Согласно (52) получим:

(61)

Однако чаще всего бывает желательно выразить относительную ошибку искомой величины через относительные ошибки величин, измеряемых в опыте, а не через абсолютные, как это сделано в формуле (61).

Для этого преобразуем каждое слагаемое в (61):

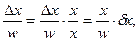
(62)

Тогда для функциональной зависимости (60) получим формулу для рас­чета ошибки:

(63)

Вполне естественно, что формулы (52) - (63) могут быть распростра­нены на любое число переменных.

Величина относительной ошибки искомой величины в (58), (59) и (63) будет выражена в процентах, если δx, δy и δz подставляются также в процентах.

Особо следует остановиться на случае, когда искомая величина w определяется как разность двух измеряемых в опыте величин, т.е.:

w= x – y

(64)

Если величины x и у близки друг другу по величине, то вслед­ствие погрешностей этих величин искомое значение w может получи­ться с очень большой ошибкой, что совершенно неприемлемо.

Разберем следующий пример. Пусть величина x = 50 и измерена с точностью ± 1, т.е. с ошибкой ± 2 %. Пусть величина y = 45 и измерена с точностью также ± 1, т.е. ошибка составляет ± 2,22 %,

Вычислим величину w совместно с максимальной абсолютной по­грешностью:

w= x – y = (50 ± 1) – (45 ± 1)= 5 ± 2.

Таким образом, несмотря на то, что погрешность в измерениях x и y так уж велика (2 и 2,22 %), погрешность в искомой величине получается очень большая, т.е.:

Применяя к этому случаю формулу (50), получаем тот же результат:

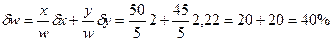
Приведенный пример показывает, что надо крайне осторожно идти на такие измерения, при которых приходится вычитать близкие друг к другу по величине числа.

В таблице. 1 приведены формулы для расчета максимально возможной относительной ошибки для некоторых функциональных зависимостей. В этой таблице через А, В, С, Д; α, β, γ и l обозначены числен­ные коэффициенты, а через x, y, z и υ - величины, непосред­ственно измеряемые в эксперименте; δx, δy, δz и δυ - от­носительные ошибки измеряемых величин, а δw - максимально воз­можная относительная ошибка искомой величины.

3. Повышение точности и вычисление вероятной ошибки при многократных измерениях.

Выше уже говорилось о том, что при проведении многократных изме­рений заданной величины при одних и тех же параметрах случайные ошибки проявляются в разбросе получаемых данных.

Если проведено несколько измерений искомой величины, то вполне
естественно, что наиболее достоверным результатом является средне­
арифметическая величина из всех измерений. Используя в качестве
окончательного результата это среднеарифметическое значение, можно
в значительной мере снизить влияние случайных ошибок при измерениях.
Естественно, что чем больше произведено измерений, тем с большей
уверенностью исключаются случайные ошибки, и в пределе при бесконечно
большом числе измерений окончательный результат будет содержать
лишь систематическую ошибку.

Абсолютная случайная ошибка при нескольких измерениях величины
вычисляется по формуле:

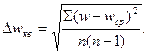
(65)

В этой формуле n - число измерений, w_cp - среднеарифмети­ческое значение из всех полученных величин w т.е.:

wcp=Σw/n

(66)

Ошибка, вычисляемая по (65), называется квадратичной. Из самого вида (52) ясно, что при n → ∞ ошибка Δw_кв → 0.

Однако функция (52) такова, что увеличение количества измере­ний с 2 до 5 сильно снижает эту ошибку; с 5 до 10 - несколько меньше, а увеличение количества измерений, например с 20 до 30, уже очень мало меняет величину этой ошибки.

Заметим, что для вычисления рассматриваемой ошибки необходимо иметь полученные в результате эксперимента величины w, что не всегда требовалось для оценки ошибки отдельного измерения.

Таблица 1

Обозначения	Расчетная формула искомой величины	Формула для определения максимально возможной относительной ошибки
а	w = A · x · y · z	δw = δx + δy + δz
б	w = A · x^α · y^β · z^γ	δw = αδx + βδy + γ δz
в		δw = αδx + βδy + γ δz + lδυ
г		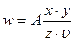δw = δx + δy + δz + δυ
д	w = x ± y ± z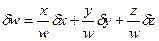
е	w = Ax ± By ± C z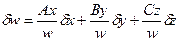
ж
з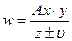
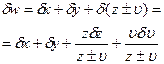
и	w = A ± Bx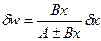
к	w = A lnx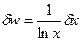
л	w = A e^α^x	δw = α x δx

Список литературы.

1. Теплотехника: Учебник для вузов / В.Н. Луканин, М.Г. Шатров и др.; под ред. В.Н. Луканина. – М.: Высш. шк., 1999 – 671 с.

2. Кудинов В.А., Карташев Э.М. Техническая термодинамика. Учебн. Пособие для вузов – М.: Высш. шк., 2000 – 261 с.

3. Стародубцев В.А. Техническая термодинамика: Учебное пособие: Омск, ОмГТУ, 1999 – 126 с.

4. Рабинович О.М. Сборник задач по технической термодинамике. М., Машиностроение, 1973 – 344 с.

5. Техническая термодинамика: Учеб. для вузов / Кириллин В.А., Сычев В.В., Шейдлин А.Е. 4-е изд. перераб. – М.: Энергоатомиздат, 1983-416 с.

6. Техническая термодинамика: Учеб. для машиностроит. спец. Вузов / Крутов В.И., Исаев С.И., Кожинов и др.; Под ред. Крутова В.И. - 3-е изд. перераб. и доп. – М.: Высш. шк., 1991 – 384 с.

Приложение I

Таблицы термодинамических свойств воды и водяного пара в состоянии насыщения (по давлениям)

Ps, бар	ts, ^oC	υ’, м^3/кг	υ”, м^3/кг	h', кДж/кг	h’’, кДж/кг	r, кДж/кг	S’ кДж/(кгК)	S’’ кДж/(кгК)
1,00 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5	99,63 102,32 104,81 107,13 109,32 111,37 113,32 115,17 116,93 118,62 120,23 121,78 123,27 124,71 126,09 127,43	0,0010434 0,0010455 0,0010476 0,00110495 0,00110513 0,0010530 0,0010547 0,0010563 0,0010579 0,0010594 0,0010608 0,0010623 0,0010636 0,0010650 0,0010663 0,0010675	1,6946 1,5501 1,4289 1,3258 1,2370 1,1597 1,0917 1,0315 0,97775 0,92951 0,88592 0,84636 0,81027 0,77724 0,74684 0,71881	417,51 428,84 439,36 449,19 458,42 467,13 475,38 483,22 490,70 497,85 504,7 511,3 517,6 523,7 529,6 535,4	2675,7 2680,0 2683,8 2687,4 2690,8 2693,9 2696,8 2699,5 2702,1 2704,6 2706,9 2709,2 2711,3 2713,3 2715,3 2717,2	2258,2 2251,2 2244,4 2238,2 2232,4 2226,8 2221,4 2216,3 2211,4 2206,8 2202,2 2197,9 2193,7 2189,5 2185,7 2181,8	1,3027 1,3330 1,3609 1,3868 1,4109 1,4336 1,4550 1,4752 1,4944 1,5127 1,5301 1,5468 1,5628 1,5781 1,5929 1,6072	7,3608 7,3288 7,2996 7,2728 7,2480 7,2248 7,2032 7,1829 7,1628 7,1458 7,1286 7,1123 7,0967 7,0819 7,0675 7,0540

Приложение II

Таблица насыщенного водяного пара

ts, ^oC	ρн, г/м^3	ps, * бар	ts, ^oC	ρн, г/м^3	ps, бар
-20 -15 -10 -5	1,10 1,39 2,14 3,24 4,84 6,80 9,40 12,82 17,29 23,03 30,36 39,59 51,13	0,00149 0,00190 0,00280 0,00410 0,00610 0,00870 0,01225 0,01692 0,0233 0,03160 0,04240 0,05780 0,0736	99,4	65,42 82,94 104,28 130,09 161,05 197,95 241,65 292,99 353,23 428,07 504,11 586,25	0,960 0,1235 0,15720 0,1985 0,2500 0,3100 0,3850 0,1710 0,5780 0,6950 0,8440 1,0100

*(1 бар = 10⁵ Па)

Приложение III

Таблица плотности перегретого водяного пара, ρ кг/м³

t,^oC p, P, бар
0,0001 0,0002 0,0003 0,0004 0,0005 0,0006 0,0007 0,0008 0,0009 0,001 0,002 0,003 0,004 0,005 0,006 0,007 0,008 0,009 0,01 0,02 0,03 0,04	0,0000795 0,000159 0,000238 0,000317 0,000397 0,000476 0,000556 0,000636 0,000715 0,000795 0,00159 0,00238 0,00317 0,00397 0,00476 - - - - - - -	0,0000782 0,0001552 0,000234 0,000313 0,000381 0,000469 0,000547 0,000526 0,000784 0,000782 0,0011552 0,00234 0,00313 0,00391 0,00469 0,00547 0,00526 - - - - -	0,0000766 0,000153 0,00023 0,000306 0,000383 0,00046 0,000536 0,000613 0,00069 0,000766 0,00153 0,00235 0,00306 0,00383 0,0046 0,00536 0,00613 0,0069 0,00766 - - -	0,0000752 0,000151 0,000235 0,000301 0,000376 0,000451 0,000526 0,000602 0,000677 0,000752 0,00151 0,00235 0,00301 0,00376 0,00451 0,00526 0,00602 0,00677 0,00752 - - -	0,0000741 0,000148 0,000222 0,000296 0,00037 0,000444 0,000528 0,000593 0,000667 0,000741 0,00148 0,00222 0,00296 0,0037 0,00444 0,00528 0,00593 0,00667 0,00741 0,0148 - -	0,0000730 0,0001455 0,000219 0,0002902 0,0003641 0,0004370 0,000510 0,0005840 0,0006506 0,000730 0,001455 0,002190 0,002902 0,003641 0,00437 0,00510 0,005840 0,006504 0,0073 0,01455 0,0219 0,02902	0,0000719 0,0002780 0,0004170 0,0005560 0,0006950 0,0008340 0,0009740 0,0001110 0,0001251 0,0007190 0,002780 0,004170 0,005560 0,006950 0,008340 0,009740 0,01110 0,01251 0,007190 0,02780 0,04179 0,05560

Приложение IV

Таблица значений относительной влажности воздуха для психрометра Августа

Показания мокрого термометра ^оС	Разность показаний сухого и мокрого термометра
0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0	10,0	11,0	12,0	13,0
0,00 2,00 4,00 6,00 8,00 10,00 12,00 14,00 16,00 18,00 20,00 22,00 24,00

Дата добавления: 2015-05-09