И методика эксперимента

ЦЕЛЕСООБРАЗНОСТЬ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ

Термодинамика изучает взаимопревращение различных видов энергии, теплоты и работы. В ее основе лежат фундаментальные законы, называемые началами или принципами термодинамики, которые были установлены путем обобщения многочисленных опытных данных. Первое начало устанавливает количественные соотношения, имеющие место при превращении энергии из одних видов в другие. Второе начало определяет условия, при которых возможны эти превращения.

Первое начало, которому и посвящена данная лабораторная работа, представляет собой закон сохранения энергии для так называемых термодинамических систем, т.е. систем, в которых существенное значение имеют тепловые процессы. Более строго, под термодинамической системой понимается совокупность макроскопических объектов (тел), обладающих внутренней энергией и способных обмениваться энергией как друг с другом, так и с внешней средой, т.е. с телами, которые являются внешними по отношению к данной системе.

Внутренняя энергия системы складывается из кинетической энергии движения ее микрочастиц и потенциальной энергии их взаимодействия. Эта энергия может изменяться как за счет совершения над системой работы, так и путем сообщения ей определенного количества теплоты. Поэтому можно говорить о двух формах передачи энергии от одного тела другому: работе и теплоте.

Работа - мера передачи механической энергии, связанная с перемещением тела как целого или взаимным перемещением отдельных его макрочастей. Теплота - это энергия, передаваемая системе внешними телами путем теплообмена, т.е. процесса обмена внутренними энергиями при контакте тел с разными температурами.

В соответствии с первым началом термодинамики теплота Q, переданная системе, идет на изменение ее внутренней энергии U и на совершение работы против внешних сил A, т.е.

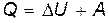. (1)

Экспериментальная проверка первого начала термодинамики, т.е. проверка справедливости уравнения (1), сопряжена с рядом значительных трудностей. Прежде всего необходимо отметить сложность измерения приращения внутренней энергии исследуемой термодинамической системы. Лишь в частном случае, когда исследуемой системой является идеальный газ, внутренняя энергия складывается только из кинетических энергий теплового движения молекул и вычисляется по формуле

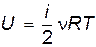, (2)

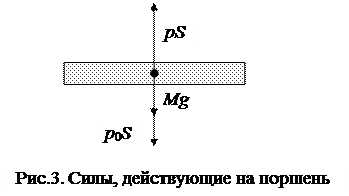
где 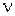- количество вещества;

R - универсальная газовая постоянная;

Т - температура газа;

i – число степеней свободы молекулы газа.

В результате экспериментальная оценка изменения внутренней энергии может быть сведена к измерению разности температур в начале и в конце процесса.

Выбрав в качестве исследуемой термодинамической системы идеальный газ, его, как правило, заключают в цилиндр под поршень, что в принципе позволяет изолировать газ от внешней среды, оценить изменение объема и измерить механическую работу, совершенную газом против внешних сил при его расширении. Однако здесь возникают новые практические трудности. Во-первых, необходимо исключить утечку газа из подпоршневого пространства и при этом ограничить силу трения, чтобы позволить поршню легко перемещаться под небольшим давлением идеального (т.е. весьма разреженного) газа. Во-вторых, весьма непросто оценить количество теплоты, полученное собственно газом, при условии, что и цилиндр, и поршень теплопроводны, обладают конечной теплоемкостью и излучательной способностью. Наконец, совсем нелегко измерить с требуемой точностью работу расширяющегося газа против внешних сил, если в эти силы входит реальная сила трения, а поршень совершает колебания относительно точек равновесия (см. ниже).

Все экспериментальные трудности легко преодолеваются при переходе от физического к имитационному эксперименту. При этом роль экспериментальной установки выполняет персональный компьютер. Его клавиатура превращается в пульт управления, а монитор совмещает роль цифровых индикаторов измерительных приборов с ролью телеэкрана, позволяющего наблюдать работу имитируемой установки как в реальном, так и машинном масштабах времени.

Имитационный эксперимент по проверке первого начала термодинамики сводится к следующему. Поршень под действием собственной силы тяжести опускается с высоты 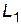до (рис.1) и сжимает воздух в цилиндре. Воздух считается идеальным двухатомным газом (число степеней свободы i =5). Перепад высот 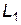- зависит как от конструктивных параметров установки (массы поршня М и площади поперечного сечения цилиндра S), так и от характера процесса сжатия газа. В данной работе моделируется изотермический процесс сжатия.

Затем сжатый под поршнем газ нагревается электронагревателем и, расширяясь, совершает работу по подъему поршня (рис.2). Высота подъема 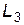- 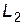зависит от количества теплоты, получаемого газом. Если при расширении газ с находящимся в нем электронагревателем термоизолирован, то высота подъема поршня будет однозначно связана с количеством электрической энергии, потребленной электронагревателем и превращенной в теплоту. Сравнивая количество теплоты, рассчитанное с использованием экспериментально полученной высоты подъема поршня, с теплотой, выделенной электронагревателем, можно оценить точность, с которой выполняется первое начало термодинамики в данном имитационном эксперименте.

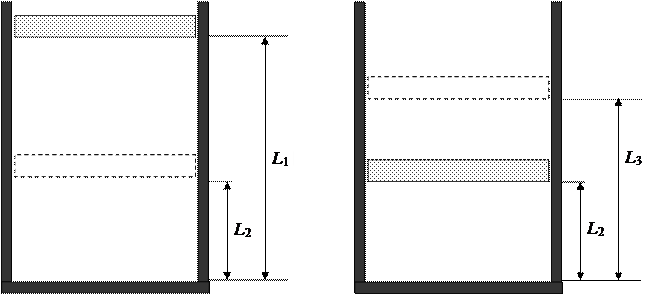Рис.1. Изотермическое сжатие Рис.2. Изобарное расширение

Особую роль в эксперименте играет сила трения. Сжатый газ ("газовая пружина") и поршень образуют пружинный маятник, колебания которого в отсутствии трения оказались бы незатухающими. Только благодаря трению возможна после нескольких колебаний остановка поршня как при его опускании под действием силы тяжести, так и при его подъеме в результате нагревания и расширения газа. В то же время из-за трения поршень останавливается не в точке равновесия, где сила давления газа и сила тяжести уравновешены, а в ее окрестности. Причем отклонение точки остановки от точки равновесия зависит от целого ряда факторов и носит во многом случайный характер. Наконец, расширяющийся газ при подъеме поршня совершает работу не только против сил тяжести и атмосферного давления, но и против сил трения.

Учитывая вышеизложенное, первое начало термодинамики для процесса расширения газа под поршнем можно, с достаточной степенью точности, записать в виде:

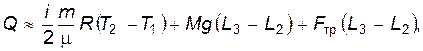(3)

где Q - количество теплоты, полученное газом;

m, 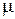- масса и молярная масса газа под поршнем, соответственно;

M - масса поршня;

g = 9,81 м/с² - ускорение свободного падения;

T ₂ - T ₁ - приращение температуры газа при его расширении;

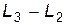- высота подъема поршня в результате расширения газа;

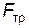- сила трения.

Приближенность уравнения (3) обусловлена тем, что в нем не учтена та часть работы газа против силы трения, которая совершается при колебаниях поршня относительно точки равновесия. Однако, учитывая небольшую амплитуду и значительную скорость затухания колебаний, это вполне допустимо (что и заложено в используемую в работе математическую модель).

До расширения газа (в положении ) и после него (в положении L ₃) на поршень действуют одни и те же взаимоуравновешивающиеся силы (рис.3): сила тяжести Мg, сила атмосферного давления p ₀ S и сила давления газа pS, запертого под поршнем. Следовательно, процесс расширения газа, сопровождающийся подъёмом поршня, можно считать изобарным и протекающим при давлении

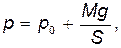(4)

где S - площадь поперечного сечения поршня и цилиндра.

Изобарность процесса позволяет выразить приращение температуры (T ₂ - T ₁) в формуле (3) через высоту подъема поршня (L ₃ - L ₂). Действительно, из уравнения Клапейрона-Менделеева следует

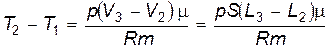, (5)

где V ₂ и V ₃ - объемы, занимаемые газом до и после его расширения, соответственно.

С учетом соотношения (5) уравнение (3) можно переписать в виде

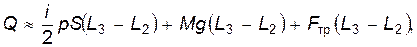(6)

а подставив в уравнение (6) соотношение (4), получим

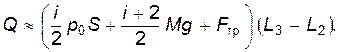(7)

В уравнении (7) параметры i, р ₀, S заданы изначально, а высоты L ₂ и L ₃ являются результирующими величинами двух последовательных имитационных экспериментов по сжатию и расширению газа в цилиндре. Силу трения следует определить предварительно, проведя специальный эксперимент, заключающийся в измерении времени падения поршня при открытом клапане в днище цилиндра. В этом случае движение поршня происходит только под действием двух противоположно направленных постоянных сил: силы тяжести Mg и силы трения F _тр. Действительно, давление газа над и под поршнем одно и то же и равно атмосферному. Вязкость воздуха при атмосферном давлении невелика, и сила сопротивления воздуха (сила вязкого трения) в условиях данного эксперимента много меньше силы тяжести и силы сухого трения. Это позволяет силой сопротивления воздуха пренебречь.

Тогда, используя второй закон Ньютона и формулу кинематики равноускоренного движения, можно записать:

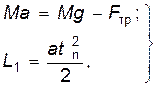(8)

откуда для силы трения получим

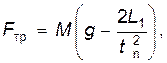(9)

где - время падения поршня с высоты L ₁ до основания цилиндра.

Итак, уравнение (7) позволяет на основе результатов трех последовательных имитационных экспериментов вычислить количество теплоты, получаемое газом от нагревателя. С другой стороны, количество электрической энергии, которую потребляет и превращает в теплоту нагреватель в ходе эксперимента, изначально задано (задаются напряжение, ток и время работы нагревателя) и определяется законом Джоуля-Ленца:

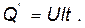(10)

Здесь необходимо напомнить, что отклонение точек остановки поршня от точек равновесия носит случайный характер. Следовательно, эксперименты по получению параметров и 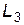следует проводить многократно, вычисляя для каждой пары экспериментов по формуле (7) величину Q. Среднее значение á Q ñ рассчитывается по формуле

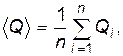(11)

где n - число пар экспериментов.

Относительная погрешность эксперимента рассчитывается по формуле:

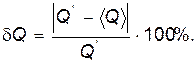(12)

Дата добавления: 2015-05-09