
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные сведения
|
|
|
|
Свойства дисперсии
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
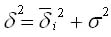
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.
1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Среднеквадрати́ческое отклоне́ние (синонимы: среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.
Измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Среднеквадратическое отклонение используют при расчёте стандартной ошибки среднего арифметического, при построениидоверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
Среднеквадратическое отклонение:
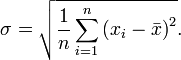
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии):
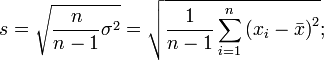
где 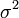 — дисперсия;
— дисперсия;  — i -й элемент выборки;
— i -й элемент выборки; 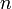 — объём выборки;
— объём выборки; 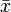 — среднее арифметическое выборки:
— среднее арифметическое выборки:

Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
[править]Правило трёх сигм
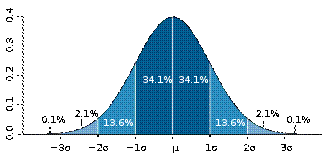

График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.
Правило трёх сигм (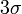 ) — практически все значения нормально распределённой случайной величины лежат в интервале
) — практически все значения нормально распределённой случайной величины лежат в интервале 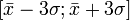 . Более строго — не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина
. Более строго — не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина 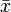 истинная, а не полученная в результате обработки выборки).
истинная, а не полученная в результате обработки выборки).
Если же истинная величина 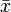 неизвестна, то следует пользоваться не
неизвестна, то следует пользоваться не  , а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.
, а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.
[править]Интерпретация величины среднеквадратического отклонения
Большое значение среднеквадратического отклонения показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределенности. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
[править]Практическое применение
На практике среднеквадратическое отклонение позволяет определить насколько значения в множестве могут отличаться от среднего значения.
[править]Климат
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного на равнине.
[править]Спорт
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит и выбираемых способов борьбы.
[править]Технический анализ
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера.
Мода — значение во множестве наблюдений, которое встречается наиболее часто. Случайная величина может не иметь моды. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.
Мода как средняя величина употребляется чаще для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, черный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.
Медиа́на (50-й процентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.
Медиана является важной характеристикой распределения случайной величины и так же, как математическое ожидание, может быть использовано для центрирования распределения. Однако, медиана более робастна и поэтому может быть более предпочтительной для распределений с т.н. тяжёлыми хвостами.
Медиана определяется для широкого класса распределений (например, для всех непрерывных), а в случае неопределённости, естественным образом доопределяется (см. ниже), в то время как математическое ожидание может быть не определено (например, у распределения Коши).
[править]Пример использования
Предположим, что в одной комнате оказалось 19 бедняков и один миллиардер. Каждый кладет на стол деньги — бедняки из кармана, а миллиардер из чемодана. По пять долларов кладет каждый бедняк, а миллиардер — $1 млрд (109). В сумме получается $1 000 000 095. Если мы разделим деньги равными долями на 20 человек, то получим $50 000 004,75. Это будетсреднее арифметическое значение суммы наличных, которая была у всех 20 человек в этой комнате.
Медиана в этом случае будет равна $5 (полусумма десятого и одиннадцатого, срединных значений ранжированного ряда). Можно интерпретировать это следующим образом. Разделив нашу компанию на две равные группы по 10 человек, мы можем утверждать, что в первой группе каждый положил на стол не больше $5, во второй же не меньше $5. В общем случае можно сказать, что медиана это то, сколько принес с собой средний человек. Наоборот, среднее арифметическое — неподходящая характеристика, так как оно значительно превышает сумму наличных, имеющуюся у среднего человека.
Коэффицие́нт асимметри́и в теории вероятностей — величина, характеризующая асимметрию распределения даннойслучайной величины.
[править]Определение
Пусть задана случайная величина 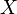 , такая что
, такая что 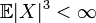 . Пусть
. Пусть  обозначает третий центральный момент:
обозначает третий центральный момент: 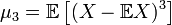 , а
, а  — стандартное отклонение
— стандартное отклонение 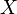 . Тогда коэффициент асимметрии задаётся формулой:
. Тогда коэффициент асимметрии задаётся формулой:
 .
.
[править]Замечания
§ Неформально говоря, коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в противном случае.
§ Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.
Коэффицие́нт эксце́сса (коэффициент островершинности) в теории вероятностей — мера остроты пика распределенияслучайной величины.
[править]Определение
Пусть задана случайная величина 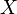 , такая что
, такая что  . Пусть
. Пусть 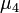 обозначает четвёртый центральный момент:
обозначает четвёртый центральный момент: 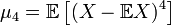 , а
, а  — стандартное отклонение
— стандартное отклонение 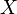 . Тогда коэффициент эксцесса задаётся формулой:
. Тогда коэффициент эксцесса задаётся формулой:
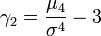 .
.
[править]Замечание
§ "Минус три" в конце формулы введено для того, чтобы коэффициент эксцесса нормального распределения был равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий.
[править]Свойства коэффициента эксцесса
§  .
.
§ Пусть 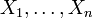 — независимые случайные величины с равной дисперсией. Пусть
— независимые случайные величины с равной дисперсией. Пусть 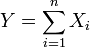 . Тогда
. Тогда
 ,
,
где 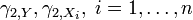 — коэффициенты эксцесса соответствующих случайных величин.
— коэффициенты эксцесса соответствующих случайных величин.
Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированнойвероятностью.
[править]Определение
Пусть есть вероятностное пространство  и
и  — вероятностная мера, задающая распределение некоторойслучайной величины
— вероятностная мера, задающая распределение некоторойслучайной величины 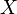 . Пусть фиксировано
. Пусть фиксировано 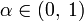 . Тогда
. Тогда 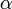 -квантилью (или квантилью уровня
-квантилью (или квантилью уровня 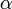 ) распределения
) распределения  называется число
называется число  , такое что
, такое что
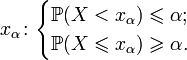
[править]Замечания
§ Если распределение непрерывно, то 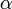 -квантиль однозначно задаётся уравнением
-квантиль однозначно задаётся уравнением
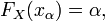
где 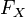 — функция распределения
— функция распределения  .
.
§ Очевидно, для непрерывных распределений справедливо следующее широко использующееся при построениидоверительных интервалов равенство:

[править]Медиана и квартили
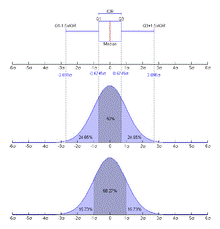

Квантили нормального распределения
Основная статья: Медиана (статистика)
§ 0,25-квантиль называется первым (или нижним) квартилем (от лат. quarta — четверть);
§ 0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым квартилем;
§ 0,75-квантиль называется третьим (или верхним) квартилем.
Интерквартильным размахом (англ. Interquartile range) называется разность между третьим и первым квартилями, то есть  . Интерквартильный размах является характеристикой разброса распределения величины и является робастныманалогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.
. Интерквартильный размах является характеристикой разброса распределения величины и является робастныманалогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.
[править]Дециль
Дециль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля от 90 % наибольших величин, лежащих выше дециля.
[править]Перцентиль
 -ой перценти́лью называют квантиль уровня
-ой перценти́лью называют квантиль уровня  . При этом обычно рассматривают перцентили для целых
. При этом обычно рассматривают перцентили для целых  , хотя данное требование не обязательно. Соответственно, медиана является 50-й перцентилью, а первый и третий квартиль — 25-й и 75-й перцентилями.
, хотя данное требование не обязательно. Соответственно, медиана является 50-й перцентилью, а первый и третий квартиль — 25-й и 75-й перцентилями.
В целом, понятия квантиль и перцентиль взаимозаменяемы, также, как и шкалы исчисления вероятностей — абсолютная и процентная.
Перцентили также называются процентилями или центилями.
[править]Квантили стандартного нормального распределения
| Уровень | 0,9999 | 0,9990 | 0,9900 | 0,9772 | 0,9750 | 0,9500 | 0,9000 | 0,8413 | 0,5000 |
| Квантиль | 3,715 | 3,090 | 2,326 | 2,000 | 1,960 | 1,645 | 1,282 | 1,000 | 0,000 |
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
[править]Определение
Пусть  — функция распределения Стьюдента
— функция распределения Стьюдента 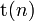 с
с 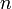 степенями свободы, и
степенями свободы, и 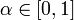 . Тогда
. Тогда 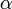 -квантилью этого распределения называется число
-квантилью этого распределения называется число 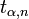 такое, что
такое, что
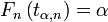 .
.
[править]Замечания
§ Прямо из определения следует, что случайная величина, имеющая распределение Стьюдента с 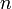 степенями свободы, не превышает значение
степенями свободы, не превышает значение 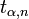 с вероятностью
с вероятностью 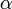 и превышает его с вероятностью
и превышает его с вероятностью 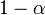 .
.
§ Функция  строго возрастает для любого
строго возрастает для любого 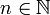 . Следовательно, определена её обратная функция
. Следовательно, определена её обратная функция  , и
, и
 .
.
§ Функция  не имеет простого представления. Однако, возможно вычислить её значения численно.
не имеет простого представления. Однако, возможно вычислить её значения численно.
§ Распределение 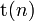 симметрично. Следовательно,
симметрично. Следовательно,
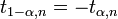 .
.
[править]Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета MATLAB. Чтобы получить значение  , необходимо найти строку, соответствующую нужному
, необходимо найти строку, соответствующую нужному  , числу степеней свободы, расчитываемому по формуле
, числу степеней свободы, расчитываемому по формуле 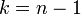 , и колонку, соответствующую нужному
, и колонку, соответствующую нужному 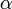 . Искомое число находится в таблице на их пересечении. Если необходимо использовать
. Искомое число находится в таблице на их пересечении. Если необходимо использовать 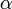 , не приведённое в таблице, то значения можно получить в табличных редакторах (в Excel функция СТЬЮДРАСПОБР; в O(L)office - TINV). Кроме того, не следует путать запись
, не приведённое в таблице, то значения можно получить в табличных редакторах (в Excel функция СТЬЮДРАСПОБР; в O(L)office - TINV). Кроме того, не следует путать запись  и
и  . Во второй записи, которая очень часто приводится в качестве ответа, речь идёт о величине "p=1-
. Во второй записи, которая очень часто приводится в качестве ответа, речь идёт о величине "p=1- 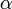 ".
".
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 1978; Нарушение авторских прав?; Мы поможем в написании вашей работы!