
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценки уравнения регрессии и его параметров
|
|
|
|
1. Индекс корреляции  :
:
 ,
, 
2. Выборочный коэффициент корреляции  :
:
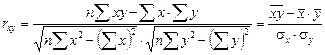 , где
, где  ;
; 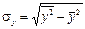 .
.
Оценивает тесноту линейной связи между переменными:
а)  связь тесная;
связь тесная;
б)  связь отсутствует;
связь отсутствует;
в)  вопрос остается открытым, нужны другие методы оценок.
вопрос остается открытым, нужны другие методы оценок.
3. Средняя ошибка аппроксимации 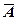 :
:

оценивает качество построенной модели. Допустимый предел значений  от 8% до 10%.
от 8% до 10%.
4. Средний коэффициент эластичности  для уравнения регрессии
для уравнения регрессии  :
:
|
 ,
,
5. Коэффициент (индекс) детерминации R 2:
 , где
, где 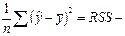 факторная дисперсия,
факторная дисперсия,
дисперсия, объясняемая уравнением регрессии, 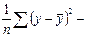 общая дисперсия.
общая дисперсия.
6. F – критерий Фишера проверки статистической незначимости уравнения регрессии:
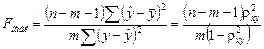 , где n – объем выборки, m – количество параметров при переменной х.
, где n – объем выборки, m – количество параметров при переменной х.
Для частного случая линейной регрессии:
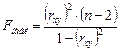 .
.
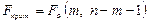 , где
, где  уровень значимости.
уровень значимости.
Если  , то уравнение регрессии ненадежно на уровне значимости
, то уравнение регрессии ненадежно на уровне значимости  .
.
Если  , то уравнение регрессии признается надежным.
, то уравнение регрессии признается надежным.
7. t – критерий Стьюдента проверки гипотезы 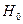 о случайной природе показателей линейной регрессии, т.е. о незначимом их отличии от нуля:
о случайной природе показателей линейной регрессии, т.е. о незначимом их отличии от нуля:


Если  , то
, то 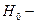 принимается, т.е. связь между х и у отсутствует на уровне значимости
принимается, т.е. связь между х и у отсутствует на уровне значимости  .
.
Если  , то
, то 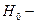 отклоняется, т.е. связь между х и у существует.
отклоняется, т.е. связь между х и у существует.
8. Доверительные интервалы параметров регрессии.
На уровне значимости  параметр
параметр 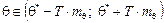 , где
, где  точечная оценка параметра
точечная оценка параметра  ,
,  табличное значение t – критерия Стьюдента, n – объем выборки, m – количество параметров при переменной х,
табличное значение t – критерия Стьюдента, n – объем выборки, m – количество параметров при переменной х,  стандартная ошибка параметра
стандартная ошибка параметра  .
.
Стандартные ошибки параметров линейной однофакторной регрессии  :
:
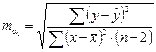


9. Построение прогнозов: В случае регрессии 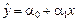 можно вычислить точечный прогноз
можно вычислить точечный прогноз  , где
, где  прогнозное значение х.
прогнозное значение х.
Доверительный интервал прогнозного значения уp:
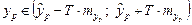 , где
, где 
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 175; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 при изменении факторной переменной х на 1% от своего среднего значения
при изменении факторной переменной х на 1% от своего среднего значения 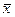 .
.